1 線性規劃概念

定義：在線性等式和不等式約束下，最小化線性目標函數。

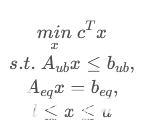
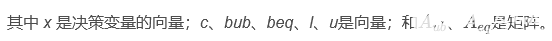
2 輸入格式

scipy．optimize．linprog（c，A_ub=None，b_ub=None，A_eq=None，b_eq=None，bounds=None，method=‘interior-point’，callback=None，options=None，x0=None）

3 參數設置

‘’‘

c：線性目標函數的系數; 數據類型：一維數組

A_ub（可選參數）：不等式約束矩陣， A_{ub} 的每一行指定 x 上的線性不等式約束的系數;數據類型：二維數組

b_ub（可選參數）：不等式約束向量，每個元素代表 A_{ub}x 的上限;數據類型：一維數組

A_eq（可選參數）：等式約束矩陣， A_{eq}的每一行指定 x 上的線性等式約束的系數;數據類型：二維數組

b_eq（可選參數）：等式約束向量，A_{eq}x 的每個元素必須等于 b_{eq} 的對應元素;數據類型：一維數組

bounds（可選參數）：定義決策變量 x 的最小值和最大值;數據類型：（min， max）序列對

None：使用None表示沒有界限，默認情況下，界限為（0，None）（所有決策變量均為非負數）

如果提供一個元組（min， max），則最小值和最大值將用作所有決策變量的界限。

method（可選參數）：算法，{‘interior-point’， ‘revised simplex’， ‘simplex’}以上三種算法可選;數據類型：輸入如上三種字符串

callback（可選參數）：調用回調函數，我的理解是等待被調用的參數 ，如果提供了回調函數，則算法的每次迭代將至少調用一次。回調函數必須接受單個 scipy．optimize．OptimizeResult由以下字段組成：

x：當前解向量; 數據類型：一維數組

fun：目標函數的當前值（c^Tx）; 數據類型：浮點數

success：當算法成功完成時為 True;數據類型：布爾值

slack：不等式約束的松弛值（名義上為正值） b_{ub} ？ A_{ub}x; 數據類型：一維數組

con：等式約束的殘差（名義上為零） b_{eq} ？ A_{eq}x;數據類型：一維數組

phase：正在執行算法的階段; 數據類型：整數

status：表示算法退出狀態的整數; 數據類型：整數

0 ： 優化按名義進行

1 ： 達到了迭代限制

2 ： 問題似乎不可行

3 ： 問題似乎是不收斂

4 ： 遇到數值困難

nit：當前的迭代次數; 數據類型：整數

message：算法狀態的字符串描述符; 數據類型：字符串

options（可選參數）——求解器選項字典，所有方法都接受以下選項：

數據類型：字典

maxiter：整數，要執行的最大迭代次數

disp：布爾值，設置為True以打印收斂消息，默認值：False

autoscale：布爾值，設置為True以自動執行平衡，如果約束中的數值分開幾個數量級，請考慮使用此選項，默認值：False

presolve：布爾值，設置為False可禁用自動預解析，默認值：True

rr：布爾值，設置為False可禁用自動移除冗余，默認值：True

x0（可選參數）：猜測決策變量的值，將通過優化算法進行優化。當前僅由’ revised simplex’ 方法使用此參數，并且僅當 x0 表示基本可行的解決方案時才可以使用此參數。 數據類型：一維數組

’‘’

4 輸出格式

‘’‘

x：在滿足約束的情況下將目標函數最小化的決策變量的值;數據類型：一維數組

fun：目標函數的最佳值（c^Tx）;數據類型：浮點數

slack：不等式約束的松弛值（名義上為正值） b_{ub}-A_{ub}x;數據類型：一維數組

con：等式約束的殘差（名義上為零）b_{eq}-A_{eq}x;數據類型：一維數組

success：當算法成功找到最佳解決方案時為 True;數據類型：布爾值

status：表示算法退出狀態的整數;數據類型：整數

0 ： 優化成功終止

1 ： 達到了迭代限制

2 ： 問題似乎不可行

3 ： 問題似乎是不收斂

4 ： 遇到數值困難

nit：在所有階段中執行的迭代總數;數據類型：整數

message：算法退出狀態的字符串描述符;數據類型：字符串 ’‘’

5 例子

import scipy

from scipy import optimize

import numpy

c = numpy．array（［2，3］） #最值等式未知數系數矩陣

A_ub = numpy．array（［［-1，1］，［2，-2］］） #《=不等式左側未知數系數矩陣

B_ub = numpy．array（［1，1］） #《=不等式右側常數矩陣

#A_eq = numpy．array（） 等式左側未知數系數矩陣

#B_eq = numpy．array（） 等式右側常數矩陣

x = （None，1） #未知數取值范圍

y = （None，None） #未知數取值范圍

res = scipy．optimize．linprog（c，A_ub，B_ub，bounds = （x，y）） #默認求解最小值，求解最大值使用-c并取結果相反數

print（res）

#結果：無解情況

con： array（［］， dtype=float64）

fun： -8782091626．64441

message： ‘The algorithm terminated successfully and determined that the problem is unbounded．’#算法成功終止，確定問題是無界的

nit： 3

slack： array（［0．89897776， 1．20204449］）

status： 3

success： False

x： array（［-1．75641833e+09， -1．75641833e+09］）

佐佑思維

審核編輯 ：李倩