閉環控制系統是現代自動控制系統的一種典型結構,對于控制專業的工程師,需要選擇合適的閉環控制器構型,找出最佳的控制參數,保證被控對象(物理系統)實現預期的行為。在所有開發階段,MATLAB 和 Simulink 都為控制系統工程師量身定做了一系列的工具,這其中自然也包括了設計和調節反饋控制器。在這個階段,工程師期望工具能夠幫助分析閉環控制的關鍵性能參數,如超調量、上升時間和穩定裕度,配平和線性化非線性模型,以及未知因素對于模型性能和穩定性的影響等等。
想要實現上述這些功能,并且得到相對“可信”的結果,就必須要有一個能夠反映真實物理系統行為的被控對象模型。在傳統控制方法,比如PID等控制器構型下,工程師需要基于線性系統理論分析閉環控制的性能,那我們也就不可避免地需要一個線性的被控對象模型。
然而“理想”很豐滿,“現實”往往確很骨感。在實際工程領域中,我們常見的被控物理系統(比如飛機、汽車、電機、液壓伺服機構),大多都是動態行為十分復雜的非線性系統。誠然我們可以通過線性化的手段,得到這些系統在穩態工況附近的線性模型,從而實現閉環控制參數的調節。但當我們把控制器的作用域放大到整個系統全工況范圍內的時候,卻發現它的性能往往不太盡如人意,特別是當系統中存在未知干擾的時候。
這是因為,當我們建立實際物理系統模型時,我們都是用一個或者幾個“確定”的數學表達來反映它的動態行為,這代表無論執行多少次仿真,我們都會針對同樣的“輸入”得到一致和確定的“結果”。但在真實物理世界中,大部分系統,特別是復雜的非線性系統,都存在一定的不確定性,這樣的不確定性普遍存在,其原因大體上可以總結為如下幾條:
建立數學模型時的簡化,比如降階;
存在未知的系統參數;
傳感器測量噪聲;
外部擾動等。
因此,控制系統的設計與實現必須考慮這樣的一個問題,即被控對象存在不確定性的情況下,反饋控制器是否仍然能夠使閉環控制穩定并能基本滿足所期望的性能指標。隨著對不確定問題越來越深刻的認識和研究,就導致了專門分析和處理具有不確定系統的控制理論,其中衍生出了兩類最具有代表性的理論:魯棒控制和自適應控制。這兩種控制方式都是基于經典線性控制理論的擴展,加入非線性因素以補償系統在階次、參數或者信號方面的非預知變化對于控制算法的影響,以達到更好的閉環控制性能。
在后續篇幅中,我們將重點討論 Simulink Control Design 對于自適應控制理論的支持,特別是在最新發布的 2022b 中,新增加的自抗擾控制器(Active Disturbance Rejection Control,ADRC)的相關內容。
01.自適應控制與 SimulinkControlDesign概述
所謂“自適應”,一般是指系統能夠按照環境的變化調整其自身,使得其行為在新的或者已經改變了的環境下達到最好,或者至少滿足預先要求的特性和功能,這種對環境變化具有適應能力的控制系統稱為自適應控制系統。自適應控制系統可以在沒有人的干預下,隨著運行環境改變而自動調節自身控制參數,以達到最優的控制。換句話說,自適應控制可以看作是一個能根據環境變化智能調節自身特性的反饋控制系統,以使系統能按照預先設定的標準,工作在最優狀態。自適應控制器內部都存在著某種學習機制,從而根據系統的運行狀態來自動更新控制參數,適用于被控對象在運行過程中動態特性變化大且帶有不確定性的情況。

圖 1-自適應控制原理示意
在 MATLAB/Simulink 中,Simulink Control Design 是為控制工程師在 Simulink 環境下進行閉環控制器設計所量身打造的工具。用戶可以基于在 Simulink 下建立的被控對象模型,開展閉環控制器的設計,或者基于 Simulink Control Design 提供的豐富資源與案例庫,快速搭建閉環控制算法原型,并通過自動代碼生成直接部署到硬件進行調整與測試,實現快速原型迭代。在最近的幾個 MATLAB 版本中,Simulink Control Design 進行了大幅的更新。在控制設計方面,基于用戶對于更先進、更智能的控制算法的應用需求,在最近的幾個版本中我們也著力改善了對自適應控制算法的支持,推出了封裝好的、直接可用的兩個自適應模塊:極值搜索控制(Extremum Seeking Control)模塊和模型參考自適應控制(Model Reference Adaptive Control)模塊,有關于這方面的介紹,可以參閱作者之前發布在公眾號上的文章。
02.ADRC模塊介紹
與 MRAC 需要參考模型不同,自抗擾控制器(ADRC)是一種不需要模型的自適應控制技術,用于處理被控對象含有未知動態特性或者內外部干擾時的閉環控制問題。ADRC 僅需要被控對象模型動態的近似估計,便可以設計無超調量的干擾抑制控制器。在新版本的 Simulink Control Design 中,提供了封裝好的 ADRC 模塊,幫助用戶在模型中快速搭建此控制算法。該模塊目前可以用一階或者二階模型近似作為已知的被控對象動態,并通過一個擴展的狀態來反映被控對象的不確定性,包括未知的動態特性和干擾。一般情況下,我們可以通過物理系統在工況范圍內的開環階躍響應特性,來確定到底是用一階模型還是二階模型來近似已知的被控對象動態。
對于一階動態近似,
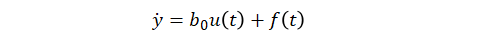
控制器具有如下結構:
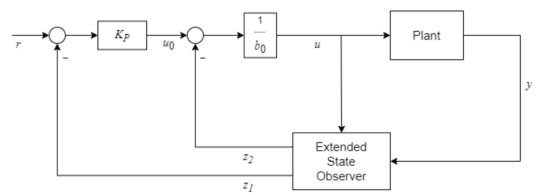
圖 2-一階動態自抗擾控制器結構
此時,控制器為基于估計狀態的狀態反饋控制器,當估計值與實際值相等時,系統為極點等于 -Kp的閉環一階系統。
對于二階動態近似,
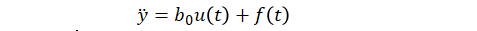
控制器具有如下結構:
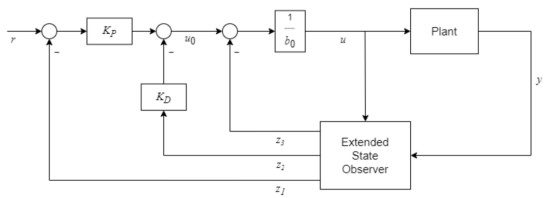
圖 3-二階動態自抗擾控制器結構
此時,控制器為基于估計狀態的狀態反饋控制器,當估計值與實際值相等時,系統為二階閉環系統。
上述公式中,y(t)、u(t)、b0和 f(t) 分別代表被控對象的輸出、輸入、近似增益和未知動態或擾動。模塊還使用了擴張狀態觀測器(Extended State Observer,ESO)來估計 f(t),通過減少估計到的擾動對于模型已知的動態近似的影響,來實現抗擾控制。
從圖2和3中可以看到,ADRC 本質上其實還是一個 PID 構型的閉環控制器,但與傳統的 PID 控制器相比,由于加入了對于系統大動態變化和未知擾動的觀測和抑制,在更加廣泛的工況范圍內,工程師在參數調節方面所需要的工作量會大幅降低(對比“增益調度”控制方式),有助于保證在非設計工作點下的閉環控制性能。
03.ADRC應用示例
如果只看上述的理論,顯得過于枯燥和晦澀的話,在新版本的 MATLAB 中,我們也提供了實際的應用示例,以展示模塊的使用方法和效果。對于上述一階和二階模型,MATLAB 分別給出了對應的示例,下面對實際工程中常用的二階系統示例做詳細介紹。對于一階系統示例,可以參閱如下的幫助文檔鏈接。
對于傳統的 PID 控制,我們可以通過頻率響應估計的方法,得到被控對象電路的線性模型,然后利用 PID Tuner,實現 PID 控制參數的調節,具體方法可以參閱軟件幫助文檔中的對應示例,在此不再贅述。
針對系統的不確定性或者擾動,我們在模型中添加了如下兩個擾動,以查看控制器對于干擾的抑制能力:
T=0.075s時的線路干擾,即輸入電壓從5V變化為10V;
T=0.09s時的負載干擾,即負載電阻從3歐姆變換為6歐姆。
ADRC 在 MATLAB/Simulink 中為封裝好的“即插即用”模塊,用戶可以通過對話框對其參數進行修改,這包括:
模型階次;
模型響應近似增益(Critical Gain);
控制器與觀測器帶寬;
控制器時域類型,這里可以選擇連續時間或者離散時間,如果要最終部署在嵌入式設備上,應選擇離散時間,并根據前面的控制器和觀測器帶寬,確定合適的采樣周期。
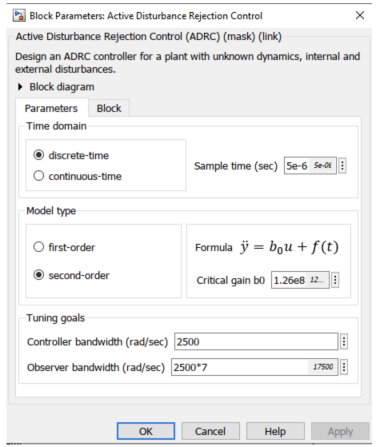
圖 5-ADRC模塊參數對話框
對于模型的階次和近似增益,我們可以利用 Simscape Electrical 建立的被控對象模型,進行開環仿真來確定,在輸入端,可以給定 Duty Cycle 為 0.5 的 PWM 驅動輸入,并截取在輸入給定后 0.0005 秒內的電壓輸出響應。
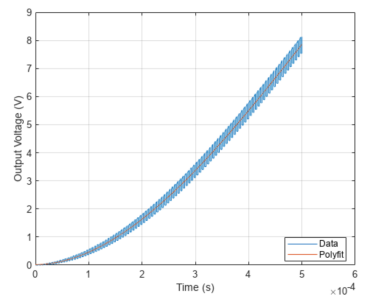
圖 6-ADRC被控對象的開環階躍響應曲線與二階曲線擬合結果
利用曲線擬合工具,我們可以得到開環系統的被控對象動態特性近似于二階系統,即
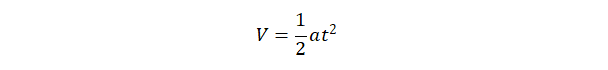
并且得到曲線中的參數,從而得到近似增益估計 b0。
對于控制器帶寬,一般取決于對控制性能的要求,而觀測器的帶寬要高于控制帶寬才能滿足控制算法部分對于觀測器結果的使用要求,一般情況,觀測器帶寬是控制帶寬的 5-10 倍,在本例中選擇了 7 倍。
仿真結果可以非常明顯地表明在輸入電壓和負載出現擾動的情況下,ADRC 與傳統 PID 相比,具有更好的抗干擾性能,閉環控制的調節時間和超調量指標都明顯更優。
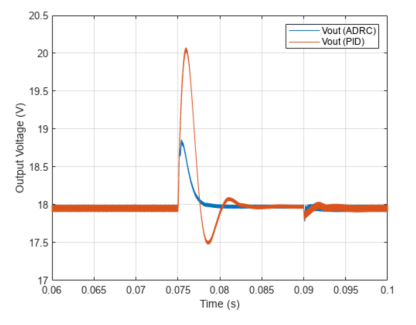
圖 7-ADRC與傳統 PID控制性能對比
寫在最后
隨著系統功能的日益復雜,以及硬件平臺處理能力的快速提升,以自適應控制為代表的先進控制理論與算法肯定會越來越多地被投入到工程應用當中。而隨著大家對物理系統特性本身和控制理論更加深入的研究,像魯棒控制、模型預測控制、模糊邏輯控制,甚至是強化學習,都將會在未來成為控制工程師口袋中的武器。MathWorks 也會持續在這些方面加大投入,除了提供對應算法理論的函數與模塊,并利用自動代碼生成實現“即插即用”外,在軟件幫助文檔中,各行業的應用案例也在逐步豐富中,幫助用戶能夠縮短學習曲線,盡快上手。如果您有相關方面的應用需求,也歡迎隨時與我們聯系!
審核編輯:郭婷
-
傳感器
+關注
關注
2552文章
51353瀏覽量
755611 -
控制器
+關注
關注
112文章
16433瀏覽量
178944 -
PID
+關注
關注
35文章
1473瀏覽量
85692
原文標題:讓控制器變“聰明” —— Simulink 自適應控制探討
文章出處:【微信號:MATLAB,微信公眾號:MATLAB】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于自適應優化的高速交叉矩陣設計
AMD Versal自適應SoC器件Advanced Flow概覽(上)

英特爾與Stellantis Motorsports攜手推進自適應控制技術
自適應電流焊接控制器:精準調控,高效焊接
空間光調制器自適應激光光束整形
步進電機如何自適應控制?步進電機如何細分驅動控制?
ALINX受邀參加AMD自適應計算峰會
如何在自己的固件中增加wifi自適應性相關功能,以通過wifi自適應認證測試?
基于非線性自適應學習控制器的四軸飛行器避障方案
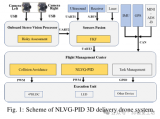




 Simulink Control Design對于自適應控制理論的支持
Simulink Control Design對于自適應控制理論的支持
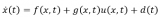











評論