通過AD采集數據時,我們總是希望采集到的數據是純凈而真實的,而實際上環境中存在太多的干擾信號,為了讓我們得到的數據盡可能地接近實際值,我們需要降低這些干擾信號的影響。所以軟件實現的數字濾波器應運而生,這一篇我們就來討論基于中值算術平均的平滑濾波器。
1、問題的提出
??在我們通過AD采集獲取數據時,不可避免會受到干擾信號的影響,而且很多時候我們希望盡可能的將這種影響減到最小。為實現這一目的,人們想了很多辦法,有硬件方面的,也有軟件方面的。在硬件難以改變或者軟件能夠達到相應效果時,我們一般采用軟件方法來實現,通常稱之為數字濾波。
??前面我們實現了基于算術平均的中值平均濾波器。這一濾波器可以解決我們一定頻率范圍內的周期性干擾和隨機性的高頻干擾。但是隨機性的干擾出現的頻次我們是不知道的,所以我們采用去掉固定數量的極大值和極小值時,雖然可以去除掉隨機干擾的部分影響,但有兩種情況還是會對我們的最終計算產生影響。其一是當隨機干擾很頻繁,我們去掉固定數量的極大值和極小值時,還會有一些受干擾的數據影響到最后的結果。其二是當隨機干擾不頻繁時,我們去掉固定數量的極大值和極小值就可能會去掉一些周期干擾所影響的數據,那么我們采用平均值的方法就不能很好的消除周期性干擾的影響。
??為了消除上述兩種情況造成的影響,我們需要改進前述的基于算術平均的中值濾波算法。我們注意到我們的每一次的測量與上一次的測量相距時間很短,數據不會有大幅度的變化,超過一定幅度的數據我們就可以認為它是受到干擾的數據,去除這些受到干擾的數據,我們就可以得到相對理想的結果。
2、算法設計
??前面我們已經描述了問題的來源,這個問題分為兩個層次。第一,我們需要去除不同種類的干擾信號,所以我們必須設計一個針對多種干擾信號的濾波算法。第二,我們需要為丟棄固定數量極大值和極小值,而造成的周期干擾的影響不平衡,導致的算術平均算法不能完全消除周期干擾。
??對于第一個層面的問題,其實與上一篇中所描述的問題是一致的。我們知道主要的干擾信號是相對頻率較低的周期干擾和相對頻率較高的非周期干擾,我們將分析這兩種信號的特點并針對性的采取相應的濾波手段。
??首先我們來考慮相對頻率較低的周期干擾,這種干擾來自于環境并且很難避免,但這種干擾信號具有一定的規律,所以它對正常信號造成的影響也是有一定規律的。我們可以圖示如下:
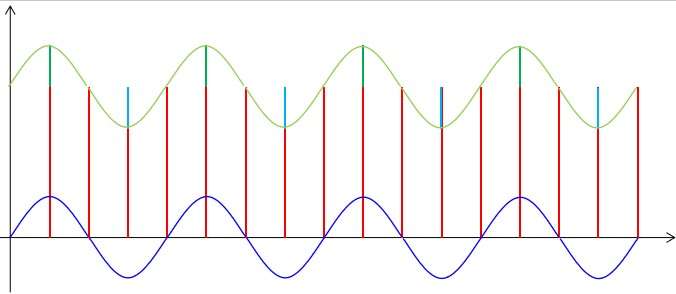
??如果只存在這一種周期性的低頻率的干擾信號,那么我們很容易想到采用算術平局算法就能夠去除,在前面我們也確實是這么做的。事實上如果存在多種頻率的周期性干擾信號,只要采集到的數據樣本數量足夠,采用算數平均算法基本都是可以得到比較理想的結果。在我們的項目中,我們的采集頻率達到了1KHz,而我們每100毫秒出一個數,所以從理論上講,10Hz以上的周期性干擾都可以通過算術平均率波來消除。
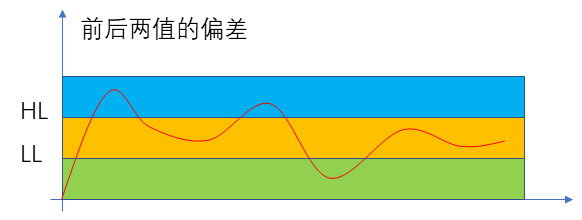
??接下來我們來考慮相對頻率較高的非周期干擾,這種干擾具有較大的隨機性,有可能對信號的影響較大,也有可能對信號的影響較小,其頻率和幅值都是隨機的,測量結果存在很大的偶然性。我們可以簡單的圖示如下:
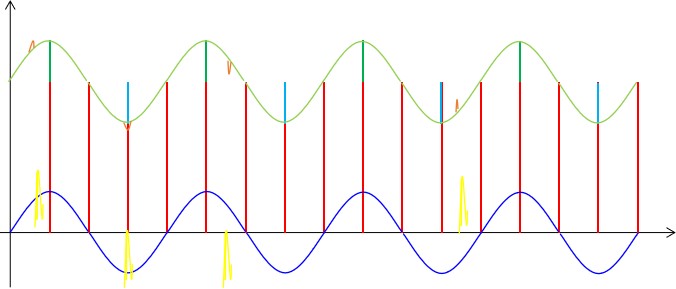
??對于這種干擾我們前面的方法對它是沒有效果的,但我們的ADC采用的是積分方式來檢測信號的,所以在兩個采樣點之間,無論這類干擾信號在何時出現都會疊加到緊接著的這個采樣數據上,致使最終的采樣數據比周期性干擾疊加的情況下要么大一些,要么小一些。這就存在兩種情況,如果是正向干擾就會是數據變大一些,如果是反向干擾就會是數據變小一些。使得最終的測量數據更加背離原始數據或者更加接近原始數據。
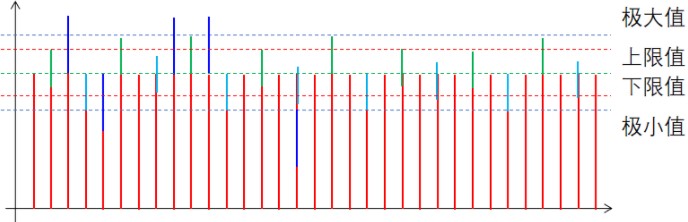
??對于更加接近我們需要的數據的變化,我們先不用理會它,畢竟它更加接近我們想要的數據。對于更加偏離的那一部分數據,我們有什么辦法將其去除掉呢?辦法是有的,我們借鑒比賽積分中去掉偶然性的方式,去掉最高和最低的數,中間的數應該更接近與真實值。具體如下圖所示:

??這樣去掉最大的一些數和最小的一些數后,并不能保證得到的就是真實的信號值,但有一點我們時刻以肯定的就是,余下的值都更為接近真實的信號值。然后我們在對余下的數采取算術平均操作,得到的就是接近真實值的一個采集值了。
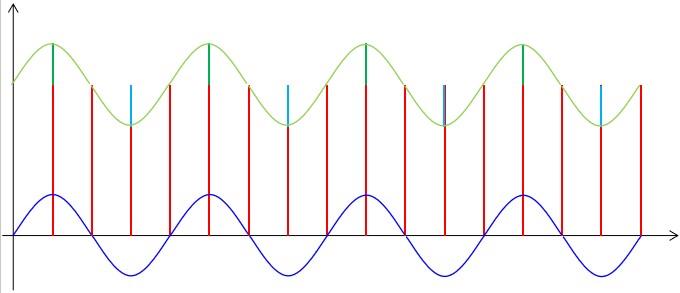
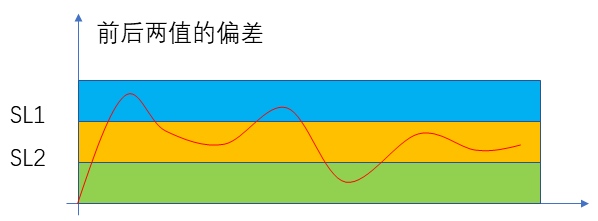
??而對于第二個層面的問題,我們考慮到我們的測量對象并不會在兩次測量之間發生劇烈的變化,所以如果某一個原始數據與上一次的測量結果偏離較大,我們就認為它是一個受到了干擾的數據,我們就將其舍棄。也就是說,以上一次的測量結果為基礎,超過上限或者下線的數據我們都認為是異常數據,具體操作圖示如下:
??事實上,這一算法不僅可以剔除劇烈變化的異常數據,對于超長周期的干擾也會有一定的抑制作用。
3、編碼實現
??上一節,我們描述了基于算術平均的限幅濾波算法,接下來我們看看具體該如何實現這一算法。根據前述的經驗,我們可以將算法的實現分為三個層次:第一,采集到足夠多的數據,并將數據排序;第二,將數據中一定數量的極大值和極小值剔除;第三,將超越限幅值的數據剔除并使用算術平均值得到最后結果。
??首先來考慮數據采集和排序的問題。數據采集速度不能太低,數據量必須達到一定的數據,約幾十至幾百的規模。考慮到數據的規模,我們依然采用簡單直接的冒泡排序實現數據的極大值和極小值的查找。
??其次我們考慮剔除極大值和極小值的問題。我們實現了對數據的排序后,剔除極大值和極小值是非常容易的,關鍵是提出的數量怎么設置。
??最后我們考慮限幅濾波的問題。我們將其超過限幅值的數據去除,并對余下的數據取算術平均。這里存在一個問題,就是如果超出限幅的數據量非常之多,遠遠超過了沒有超限的數據量該怎么辦呢?我們認為這使得數據也許真的是因為某些原因而出現了較大的變化。此時我們將對全體數據取算術平均值,以快速響應檢測對象的變化。
??根據上述的描述,我們可以實現算法如下:
/*限幅平均濾波算法*/
static uint32_t LimitedMeanFilter(uint32_t *pData,uint16_t aSize,uint16_t eSize,uint32_t rData,uint32_t lValue)
{
uint32_t tData;
uint32_t uResult=0;
uint32_t mResult=0;
uint32_t lResult=0;
uint16_t uNumber=0;
uint16_t mNumber=0;
uint16_t lNumber=0;
if(aSize<=2*eSize)
{
return 0;
}
for (int i=0; i-1; i++) //比較n-1輪
{
for (int j=0; j-1-i; j++) //每輪比較n-1-i次,
{
if (pData[j] < pData[j+1])
{
tData = pData[j];
pData[j] = pData[j+1];
pData[j+1] = tData;
}
}
}
for(int j=eSize;j<(aSize-eSize);j++)
{
if(pData[j]>(rData+lValue))
{
uResult=uResult+pData[j];
uNumber++;
}
else if(pData[j]<(rData-lValue))
{
lResult=lResult+pData[j];
lNumber++;
}
else
{
mResult=mResult+pData[j];
mNumber++;
}
}
if((mNumber>uNumber)&&(mNumber>lNumber))
{
mResult = mResult/mNumber;
}
else
{
mResult = (uResult+mResult+lResult)/(uNumber+mNumber+lNumber);
}
return mResult;
}
??在上述實現中,我們先對輸入的數據進行了排序。然后我們去除了一定數量的極大值和極小值,并檢測余下的值是否超越了限幅值。并對限幅之內、超越上限及超越下限的數據分別求和。然后判斷三類數據的數量,當限幅內數據的數量超過三分之一時,對其取算術平均,否則對所有數據取算術平均。
??對于函數中的五個參數:uint32_t *pData是需要濾波的原始采集數據;uint16_t aSize是需要濾波的原始采集數據的數量;uint16_t eSize是需要丟棄的極大值和極小值的數量。其中aSize要遠大于eSize的2倍,否則大部分被舍棄,濾波的意義就不大了。uint32_t rData參數是參考值;uint32_t lValue參數是偏離參考值的限幅。
??函數的使用也很簡單。比如在我們的應用中,我們以1KHz的速度采集原始值,每采集100個數出一個測量結果,去掉10個極大值和10個極小值,于是我們就可以調用函數如下:
temp[i]=LimitedMeanFilter(rDatas[i],100,10,refData[aPara.phyPara.waveband][i],150);
??在這個應用中,我們測試去掉10個極大值和10個極小值,并將限幅的偏差設置為了150,當然這些數值的取值根據具體的應用而定。特別是參考數據的選擇非常關鍵,一般可以根據不同的情況選取上一個測量結果、一定數量的之前的測量結果的算術平均或加權平均,或者采用累計的平均值等。
4、應用總結
??這一篇中,我們實現了基于算術平均的限幅濾波器。該濾波器對一定頻率以上的周期性干擾和隨機性的噪聲干擾均有較好的效果。通過修改丟棄的極大值和極小值的數量可以應對在不同環境下的濾波要求。也可以對超長周期的干擾和其它原因造成的劇變數據擁有較好的抑制作用。
??對于限幅的取值一般只能根據采集系統的特點或者工程師的經驗來判斷,但并非是盲目的,因為很多情況下我們是能夠判斷出干擾信號的大致判斷范圍的。所以限幅值的選取,以及剔除的極大極小值的數量都需要根據集體的應用場景來設置。
??此外參考值的選取也會對濾波效果有決定性影響。一般根據具體的應用場景我們可以選取上一個測量結果、一定數量的之前的測量結果的算術平均或加權平均,或者采用累計的平均值等作為參考值。
-
濾波器
+關注
關注
161文章
7843瀏覽量
178378 -
數字濾波器
+關注
關注
4文章
270瀏覽量
47044 -
算法設計
+關注
關注
0文章
24瀏覽量
8169
發布評論請先 登錄
相關推薦
基于算術平均算法的中值數字濾波器設計
基于算術平均值的網絡流量數據采樣方法
十一個經典的濾波算法的介紹和示例程序詳細資料免費下載
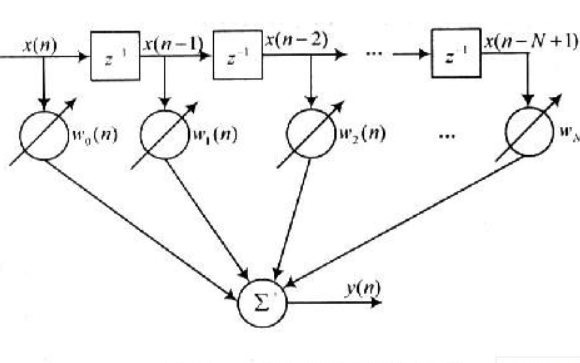




 基于算術平均算法的限幅濾波器設計
基于算術平均算法的限幅濾波器設計
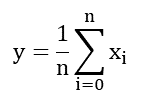











評論