大規(guī)模 3D 重建的Power Bundle Adjustment
筆者個(gè)人理解
我們知道BA問題本質(zhì)上是求解增量線性方程的方程,在BA中H矩陣有著其特殊的結(jié)構(gòu)
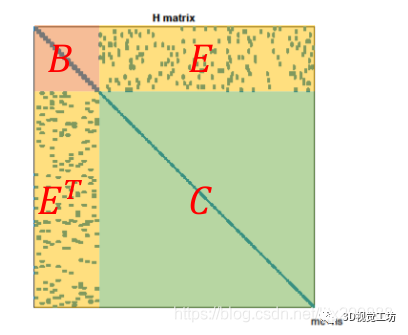
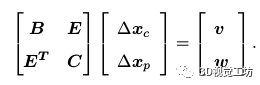
其中B,C是對(duì)角塊矩陣,C的規(guī)模遠(yuǎn)大于B,對(duì)角塊矩陣求逆的難度遠(yuǎn)小于普通矩陣,故而我們可以將其簡(jiǎn)化為
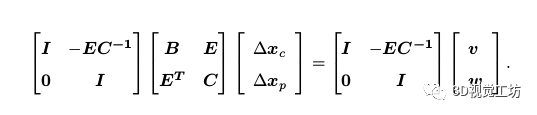
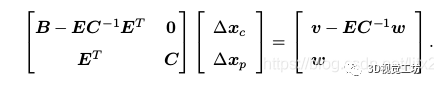
這樣第一行方程就變?yōu)榕cxp無(wú)關(guān)的項(xiàng)
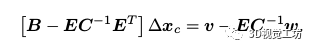
求解出,代入到第二個(gè)方程,利用C矩陣易于求逆的性質(zhì),快速求解出。
很明顯,在整個(gè)過程中耗時(shí)最多的便是求解Schur 補(bǔ)消元后的第一個(gè)方程。在這篇論文中作者提出了利用冪級(jí)數(shù)的方法來(lái)加速求解第一個(gè)方程,下面可以和筆者一起來(lái)看一下具體的實(shí)現(xiàn)方式。
摘要
我們引入 Power Bundle Adjustment 作為一種擴(kuò)展型算法,用于解決大規(guī)模BA問題。它基于逆 Schur 補(bǔ)的冪級(jí)數(shù)展開,構(gòu)成了我們稱之為逆展開方法的新求解器家族。我們從理論上證明了冪級(jí)數(shù)的使用是正確的,并且證明了我們方法的收斂性。使用真實(shí)世界的 BAL 數(shù)據(jù)集,我們表明所提出的求解器挑戰(zhàn)了最先進(jìn)的迭代方法,并顯著加快了法方程的求解速度,即使達(dá)到了非常高的精度。這個(gè)易于實(shí)施的求解器還可以補(bǔ)充最近提出的分布式BA框架。我們證明,使用建議的power BA作為子問題求解器可以顯著提高分布式優(yōu)化的速度和準(zhǔn)確性
1、介紹
BA (BA) 是一個(gè)經(jīng)典的計(jì)算機(jī)視覺問題,它構(gòu)成了許多 3D 重建和運(yùn)動(dòng)結(jié)構(gòu) (SfM) 算法的核心組成部分。它指的是通過最小化非線性重投影誤差來(lái)聯(lián)合估計(jì)相機(jī)參數(shù)和 3D 地標(biāo)位置。最近出現(xiàn)的大規(guī)模互聯(lián)網(wǎng)照片集 [1] 提出了對(duì)在運(yùn)行時(shí)和內(nèi)存方面可擴(kuò)展的 BA 方法的需求。為增強(qiáng)現(xiàn)實(shí)或自動(dòng)駕駛等應(yīng)用構(gòu)建準(zhǔn)確的城市比例地圖使當(dāng)前的 BA 方法達(dá)到了極限
由于正規(guī)方程的求解是 BA 中最耗時(shí)的步驟,因此通常采用 Schur 補(bǔ)技巧來(lái)形成縮減相機(jī)系統(tǒng)(RCS)。這個(gè)線性系統(tǒng)只涉及位姿參數(shù)并且明顯更小。通過使用 QR 因式分解,僅導(dǎo)出 RCS 的矩陣平方根,然后求解代數(shù)等價(jià)問題 [4],可以進(jìn)一步減小其大小。RCS 及其平方根公式通常通過迭代方法求解,例如針對(duì)大規(guī)模問題的流行預(yù)處理共軛梯度算法,或通過直接方法(例如針對(duì)小規(guī)模問題的 Cholesky 分解)求解
在下文中,我們將依靠逆 Schur 補(bǔ)的迭代逼近來(lái)挑戰(zhàn)這兩個(gè)求解器系列。特別是,我們的貢獻(xiàn)如下:
? 我們?yōu)楦咝У拇笠?guī)模 BA 引入了power BA (PoBA)。我們稱之為逆擴(kuò)展方法的這一新技術(shù)系列挑戰(zhàn)了建立在迭代和直接求解器上的最先進(jìn)的方法。
? 我們將boundle adjustment問題與冪級(jí)數(shù)理論聯(lián)系起來(lái),我們提供了證明這種擴(kuò)展合理的理論證明,并建立了求解器的收斂性。
? 我們對(duì)BAL 數(shù)據(jù)集上提出的方法進(jìn)行了廣泛的評(píng)估,并與幾個(gè)最先進(jìn)的求解器進(jìn)行了比較。我們強(qiáng)調(diào)了 PoBA 在速度、準(zhǔn)確性和內(nèi)存消耗方面的優(yōu)勢(shì)。圖 1 顯示了 97 個(gè)評(píng)估的 BAL 問題中的兩個(gè)的重建。
? 我們將我們的求解器合并到最近提出的分布式 BA 框架中,并在速度和準(zhǔn)確性方面顯示出顯著的改進(jìn)。
? 我們將求解器作為開源軟件發(fā)布,以促進(jìn)進(jìn)一步研究。
2、相關(guān)的工作
由于我們提出了一種求解大規(guī)模BA的新方法,我們將回顧BA和傳統(tǒng)求解方法,即直接法和迭代法的工作。我們還提供了一些關(guān)于冪系列的背景知識(shí)。關(guān)于級(jí)數(shù)擴(kuò)展的一般介紹,我們請(qǐng)讀者參考[14]。
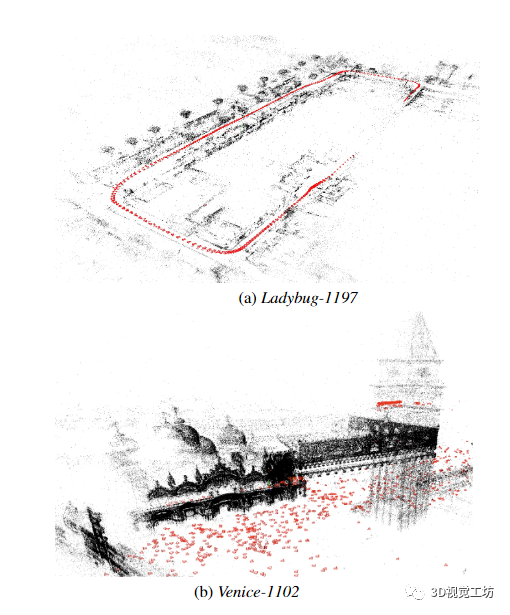
圖 1. Power Bundle Adjustment (PoBA) 是一種針對(duì)大規(guī)模 BA 問題的新型求解器,它比現(xiàn)有求解器速度快得多,內(nèi)存效率更高。(a) 具有 1197 個(gè)姿勢(shì)的瓢蟲 BAL 問題的優(yōu)化 3D 重建。PoBA-32(分別為 PoBA-64)比最佳競(jìng)爭(zhēng)求解器快 41%(分別為 36%)以達(dá)到 1% 的成本容差。(b) 具有 1102 個(gè)姿勢(shì)的 Venice BAL 問題的優(yōu)化 3D 重建。PoBA-32(分別為 PoBA-64)比最佳競(jìng)爭(zhēng)求解器快 71%(分別為 69%)以達(dá)到 1% 的成本容忍度。PoBA 的內(nèi)存消耗是√BA(resp. Ceres)的五倍(resp.兩倍)。
2.1可擴(kuò)展的boundle adjustment
boundle adjustment的詳細(xì)調(diào)查可以在 [16] 中找到。Schur 補(bǔ)碼 [20] 是利用 BA 問題稀疏性的普遍方法。分辨率方法的選擇通常由正規(guī)方程的大小決定:隨著大小的增加,稀疏和密集 Cholesky 分解 [15] 等直接方法的性能優(yōu)于不精確牛頓算法等迭代方法。具有數(shù)萬(wàn)張圖像的大規(guī)模BA問題通常通過共軛梯度法 [1, 2, 8] 來(lái)解決。已經(jīng)設(shè)計(jì)了一些變體,例如可以擴(kuò)大搜索空間 [17] 或可以使用基于可見性的預(yù)調(diào)節(jié)器 [9]。最近一系列關(guān)于平方根BA的工作建議用零空間投影 [4、5] 代替 Schur 補(bǔ)碼來(lái)消除地標(biāo)。它導(dǎo)致顯著的性能改進(jìn),并在速度和準(zhǔn)確性方面成為boundle adjustment問題的最佳性能求解器之一。盡管如此,這些方法仍然依賴于傳統(tǒng)的求解器來(lái)解決減少的相機(jī)系統(tǒng)問題,即用于大規(guī)模 [4] 的預(yù)處理共軛梯度法 (PCG) 和用于小規(guī)模 [5] 問題的 Cholesky 分解,此外還有一個(gè)重要的成本內(nèi)存消耗術(shù)語(yǔ)。即使使用 PCG,求解正規(guī)方程仍然是瓶頸,找到數(shù)千個(gè)未知參數(shù)需要大量的內(nèi)部迭代。其他作者試圖通過關(guān)注高效并行化 [13] 來(lái)提高 PCG BA 的運(yùn)行時(shí)間。最近,隨機(jī) BA [22] 被引入以將減少的相機(jī)系統(tǒng)隨機(jī)分解為子問題,并通過密集分解求解較小的正規(guī)方程。這導(dǎo)致了具有改進(jìn)的速度和可擴(kuò)展性的分布式優(yōu)化框架。通過將一般冪級(jí)數(shù)理論封裝到線性求解器中,我們建議同時(shí)提高這些現(xiàn)有方法的速度、準(zhǔn)確性和內(nèi)存消耗。
2.2冪級(jí)數(shù)求解器。
雖然冪級(jí)數(shù)展開常用于求解微分方程 [3],但據(jù)我們所知,它從未用于求解BA問題。最近的一項(xiàng)工作 [21] 將 Schur 補(bǔ)碼與 Neumann 多項(xiàng)式展開聯(lián)系起來(lái),以構(gòu)建一個(gè)新的預(yù)條件器。盡管這種方法對(duì)某些物理問題(例如對(duì)流擴(kuò)散或大氣方程)給出了有趣的結(jié)果,但它對(duì)于BA問題仍然不能令人滿意(見圖 2)。相反,我們建議直接應(yīng)用逆 Schur 補(bǔ)的冪級(jí)數(shù)展開來(lái)解決 BA 問題。因此,我們的求解器屬于擴(kuò)展方法的范疇——據(jù)我們所知——從未應(yīng)用于 BA 問題。除了是一個(gè)易于實(shí)現(xiàn)的求解器之外,它還利用 BA 問題的特殊結(jié)構(gòu)來(lái)同時(shí)提高現(xiàn)有方法的權(quán)衡速度精度和內(nèi)存消耗
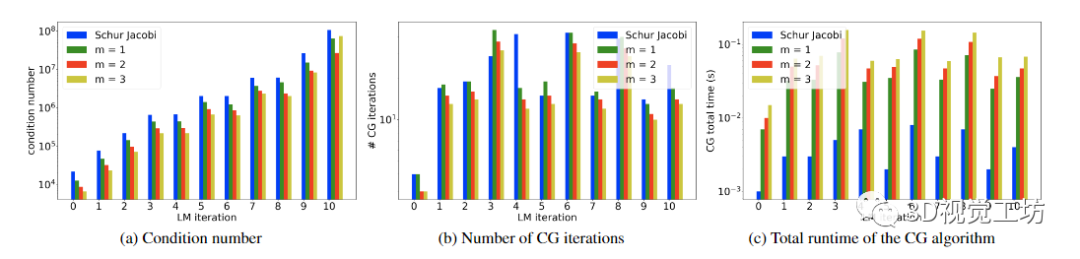
圖 2. 盡管 [21] 探討了使用冪級(jí)數(shù)作為某些物理問題的預(yù)條件子,但它受到 BA 公式的特殊結(jié)構(gòu)的影響。給定預(yù)處理器 M -1 和 Schur 補(bǔ)碼 S,條件數(shù) κ(M -1S) 與共軛梯度算法的收斂性相關(guān)聯(lián)。(a) 說明了 LM 算法針對(duì)實(shí)際問題 Ladybug-49 的第 10 次迭代的行為,其中具有來(lái)自 BAL 數(shù)據(jù)集的 49 個(gè)姿勢(shì),并且對(duì)于用作 CG 算法預(yù)條件子的冪級(jí)數(shù)展開 (22) 的不同階數(shù) m 。與流行的 Schur-Jacobi 預(yù)條件子相關(guān)的條件數(shù)通過這個(gè)冪級(jí)數(shù)預(yù)條件子減少了,這通過 CG 算法更好的收斂和更少的 CG 迭代次數(shù) (b) 來(lái)說明。然而,由于冪級(jí)數(shù)預(yù)條件器的應(yīng)用涉及 4m 矩陣向量乘積,因此每個(gè)補(bǔ)充階 m 在運(yùn)行時(shí)方面的成本更高,而 Schur-Jacobi 預(yù)條件器可以有效地存儲(chǔ)和應(yīng)用。(c) 導(dǎo)致求解正規(guī)方程 (6) 時(shí)的總運(yùn)行時(shí)間增加。
3、冪級(jí)數(shù)
我們簡(jiǎn)要介紹矩陣的冪級(jí)數(shù)展開。令 ρ(A) 表示方陣 A 的譜半徑,即最大絕對(duì)特征值,并用‖A‖ = ρ(A) 表示譜范數(shù)。以下命題成立
命題 1. 令 M 為 n × n 矩陣。若M的譜半徑滿足‖M‖《1,則
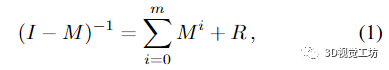
其中誤差矩陣
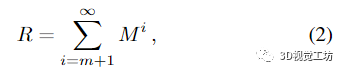
滿足
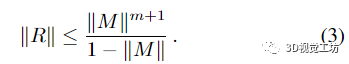
附錄給出了證明,圖5給出了實(shí)際問題的說明
4、power BA
我們考慮具有 np 個(gè)位姿和 nl 個(gè)地標(biāo)的BA的一般形式。令 x = (xp, xl) 為包含所有優(yōu)化變量的狀態(tài)向量,其中長(zhǎng)度為 dp*np 的向量 xp 與所有姿勢(shì)的外部和(可能)內(nèi)部相機(jī)參數(shù)相關(guān)聯(lián),長(zhǎng)度為 3*nl 的向量 xl 與所有地標(biāo)的 3D 坐標(biāo)。如果只有外部參數(shù)未知,則 dp = 6 用于每個(gè)攝像機(jī)的旋轉(zhuǎn)和平移。對(duì)于評(píng)估的 BAL 問題,我們另外估計(jì)內(nèi)在參數(shù)和 dp = 9。目標(biāo)是最小化總BA能量
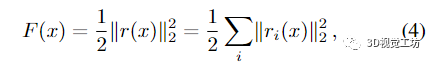
其中向量 r(x) = [r1(x), 。.., rk(x)] 包含捕獲模型和觀察之間差異的所有殘差。
4.1.最小二乘問題
這種非線性最小二乘問題通常使用 Levenberg-Marquardt (LM) 算法求解,該算法基于當(dāng)前狀態(tài)估計(jì)值 x0 = (x0 p, x0 l ) 的一階泰勒近似 r(x)。通過添加正則化項(xiàng)來(lái)提高收斂性,最小化變成
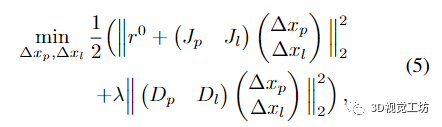
其中
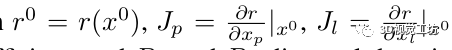
λ 是阻尼系數(shù),Dp 和 Dc 是位姿和地標(biāo)變量的對(duì)角阻尼矩陣。這個(gè)阻尼問題導(dǎo)致相應(yīng)的正規(guī)方程
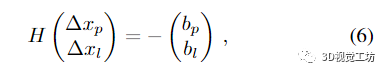
這里
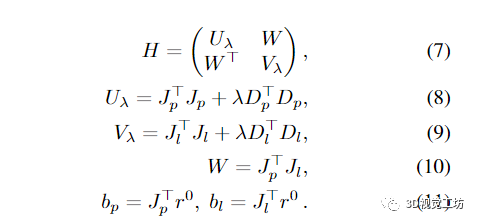
Uλ、Vλ 和 H 是對(duì)稱正定的 [16]
4.2.舒爾補(bǔ)
由于直接反演大小為(dpnp+3nl)2的系統(tǒng)矩陣H對(duì)于大規(guī)模問題往往代價(jià)過高,因此通常使用Schur補(bǔ)碼技巧進(jìn)行約簡(jiǎn)。其想法是形成約簡(jiǎn)相機(jī)系統(tǒng)
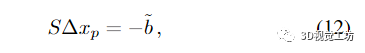
同時(shí)
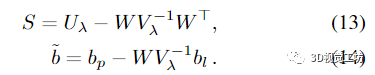
然后求解 (12) 的 Δxp。最優(yōu)的 Δxl 是通過回代獲得的
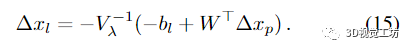
4.3.power BA
用分塊矩陣 Uλ 對(duì) (13) 進(jìn)行因式分解
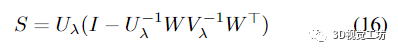
導(dǎo)致將逆 Schur 補(bǔ)表示為
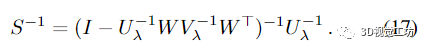
為了將 (17) 展開為命題 1 中詳述的冪級(jí)數(shù),我們需要將的光譜半徑限制為 1
通過利用 BA 問題的特殊結(jié)構(gòu),我們證明了一個(gè)更強(qiáng)大的結(jié)果:
引理 1. 令 μ 為的特征值。然后

證明: 一方面, 是對(duì)稱正半定的,因?yàn)?Uλ 和 Vλ 是對(duì)稱正定的。則其特征值大于 0。由于 與 》 相似,

另一方面, 與 S 和 Uλ 一樣是對(duì)稱正定的。因此,由于 的相似性,U ?1 λ S 的特征值都嚴(yán)格為正。作為
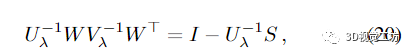
它遵循

證明結(jié)束。
假設(shè)
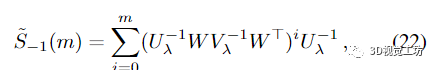
并且
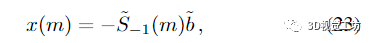
對(duì)于 m ≥ 0。以下命題證實(shí)了近似值確實(shí)隨著 m 的遞增階數(shù)收斂:
命題2
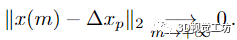
證明。我們表示 P = 。由于引理 1

與 (6) 關(guān)聯(lián)的逆 Schur 補(bǔ)允許冪級(jí)數(shù)展開:
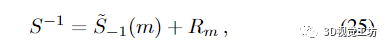
這里
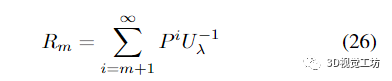
滿足
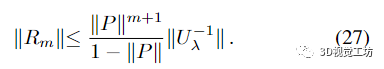
由此得出
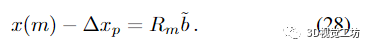
譜范數(shù)相對(duì)于矢量范數(shù)的一致性意味著:
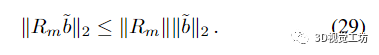
從(24)、(27)和(29)我們得出證明
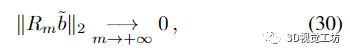
所以
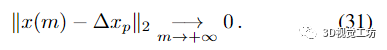
該收斂結(jié)果證明:
? 將(22) 應(yīng)用于(12) 的右側(cè)可以直接獲得Δxp 的近似值;
? 這種近似的質(zhì)量取決于階數(shù) m 并且可以根據(jù)需要盡可能小
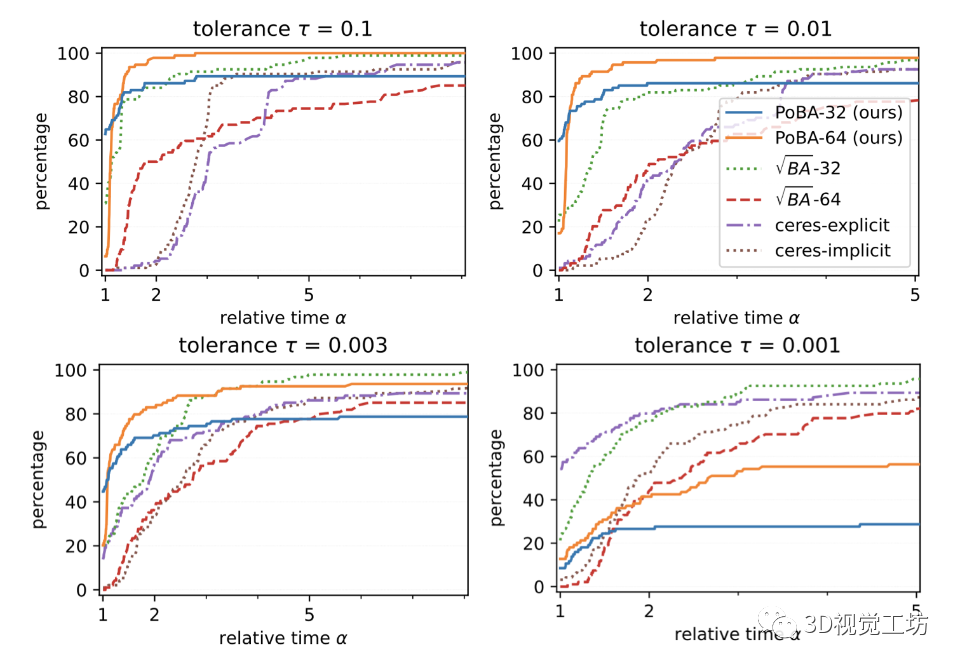
圖 3. 所有 BAL 問題的性能概況顯示解決給定精度公差 τ ∈ {0.1, 0.01, 0.003, 0.001} 和相對(duì)運(yùn)行時(shí)間 α 的問題的百分比。我們提出的求解器 PoBA 使用 Schur 補(bǔ)數(shù)的級(jí)數(shù)展開顯著優(yōu)于所有競(jìng)爭(zhēng)求解器,精度可達(dá) τ = 0.003。
冪級(jí)數(shù)展開是迭代導(dǎo)出的,需要終止規(guī)則。
通過類比不精確的牛頓法 [11, 12, 18] 這樣共軛梯度算法我們?cè)O(shè)置了一個(gè)停止標(biāo)準(zhǔn)
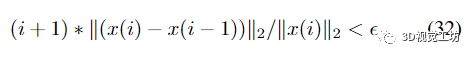
對(duì)于給定的。該標(biāo)準(zhǔn)確保當(dāng)通過將逆 Schur 補(bǔ)碼擴(kuò)展為補(bǔ)充順序來(lái)更新位姿的細(xì)化時(shí),冪級(jí)數(shù)擴(kuò)展停止
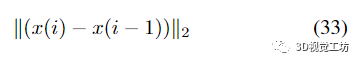
達(dá)到同階時(shí)遠(yuǎn)小于平均細(xì)化
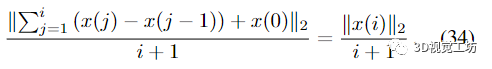
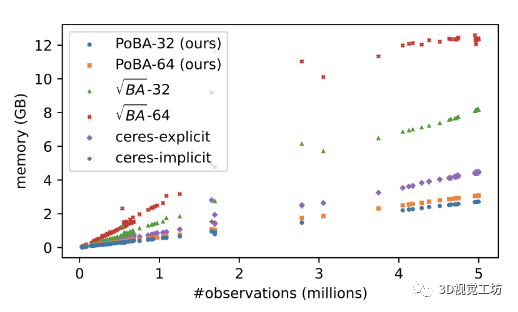
圖 4. 所有 BAL 問題的內(nèi)存消耗。所提出的 PoBA 求解器(橙色和藍(lán)色點(diǎn))的內(nèi)存消耗比 √BA 求解器少五倍
5、實(shí)現(xiàn)
我們直接在 [4] 的公開可用實(shí)現(xiàn) 1 上以單 (PoBA-32) 和雙 (PoBA-64) 浮點(diǎn)精度在 C++ 中實(shí)現(xiàn)我們的 PoBA 求解器。這個(gè)最近的求解器通過使用具有里程碑意義的雅可比行列式的 QR 因式分解,表現(xiàn)出出色的性能來(lái)解決boundle adjustment。它尤其與流行的 Ceres 求解器競(jìng)爭(zhēng)。我們還添加了與 Ceres 的稀疏 Schur 補(bǔ)碼求解器的比較,類似于 [4]。Ceres-explicit 和 Ceres-implicit 使用由 Schur-Jacobi 預(yù)調(diào)節(jié)器預(yù)處理的共軛梯度算法迭代求解 (12)。第一個(gè)將 S 作為塊稀疏矩陣保存在內(nèi)存中,第二個(gè)在迭代期間即時(shí)計(jì)算 S。√BA 和 Ceres 提供了非常有競(jìng)爭(zhēng)力的性能來(lái)解決boundle adjustment問題,這使得它們與 PoBA 相比非常具有挑戰(zhàn)性的基線。我們?cè)?MacOS 11.2 上運(yùn)行實(shí)驗(yàn),配備 Intel Core i5 和 4 個(gè)內(nèi)核,頻率為 2GHz。
高效存儲(chǔ)
我們利用 BA 問題的特殊結(jié)構(gòu)并設(shè)計(jì)了內(nèi)存高效存儲(chǔ)。我們按地標(biāo)對(duì)雅可比矩陣和殘差進(jìn)行分組,并將它們存儲(chǔ)在單獨(dú)的密集內(nèi)存塊中。對(duì)于具有 k 個(gè)觀察值的地標(biāo),所有與觀察到地標(biāo)的姿勢(shì)相對(duì)應(yīng)的大小為 2 × dp 的雅可比位姿塊被堆疊并存儲(chǔ)在大小為 2k × dp 的內(nèi)存塊中。連同大小為 2k × 3 的地標(biāo)雅可比塊和長(zhǎng)度為 2k 的殘差也與地標(biāo)相關(guān)聯(lián),單個(gè)地標(biāo)的所有信息都有效地存儲(chǔ)在大小為 2k × (dp + 4) 的內(nèi)存塊中。此外,(15)和(23)中涉及的操作使用內(nèi)存塊并行化。
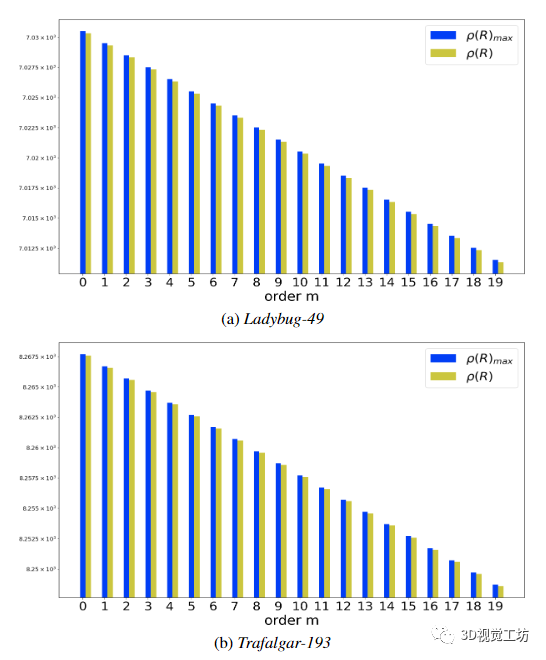
圖 5. 兩個(gè) BAL 問題的第一次 LM 迭代的命題 1 中的不等式 (3) 的圖示:(a) 具有 49 個(gè)姿勢(shì)的瓢蟲和 (b) 具有 193 個(gè)姿勢(shì)的特拉法加。當(dāng) m 《 20 時(shí),誤差矩陣 R 的譜范數(shù)以綠色繪制。以藍(lán)色繪制的不等式右側(cè)表示誤差矩陣譜范數(shù)的理論上限,并且取決于所考慮的 m 和譜M 的范數(shù) = U ?1 λ W V ?1 λ W 》。對(duì)于光譜庫(kù) [23],ρ(M) 取值 (a) L-49 的 0.999858 和 (b) T-193 的 0.999879。兩個(gè)值都小于 1,并且 ρ(R) 始終小于 ρ(M )m+1/(1 ? ρ(M )),如引理 1 中所述。
性能概況
為了比較一組求解器,用戶可能對(duì)兩個(gè)因素感興趣,即運(yùn)行時(shí)間更短和精度更高。性能配置文件 [6] 對(duì)兩者進(jìn)行聯(lián)合評(píng)估。設(shè) S 和 P 分別是一組求解器和一組問題。令 f0(p) 為初始目標(biāo),f (p, s) 為求解器 s ∈ S 在求解問題 p ∈ P 時(shí)達(dá)到的最終目標(biāo)。S 中求解器針對(duì)問題 p 達(dá)到的最小目標(biāo)是 f ?(p) = mins∈S f (p, s)。給定公差 τ ∈ (0, 1),問題 p 的目標(biāo)閾值由下式給出
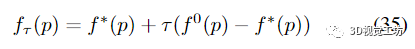
求解器達(dá)到這個(gè)閾值所需的運(yùn)行時(shí)間被記錄為T√(p, s)。很明顯,對(duì)于給定問題p,最有效的求解器s*達(dá)到閾值時(shí),運(yùn)行時(shí)T運(yùn)行時(shí)T會(huì)用(p, s*)=min 2 2 S T會(huì)用(p, s)。然后,相對(duì)運(yùn)行時(shí)α的求解器的性能文件被定義為
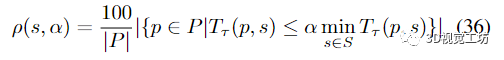
在圖形上,給定求解器的性能概況是解決問題的百分比快于 x 軸上的相對(duì)運(yùn)行時(shí)間 α
5.1.實(shí)驗(yàn)設(shè)置
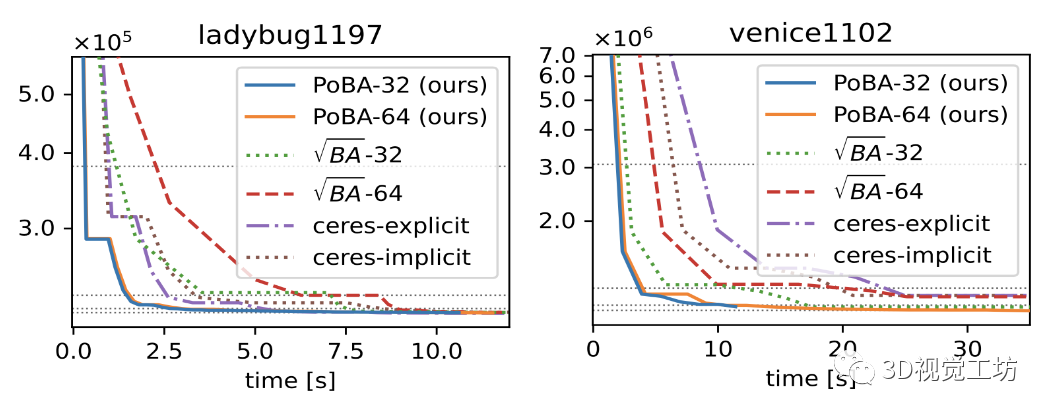
圖 6. 來(lái)自具有 1197 個(gè)姿勢(shì)的 BAL 數(shù)據(jù)集的 Ladybug-1197(左)和來(lái)自具有 1102 個(gè)姿勢(shì)的 BAL 數(shù)據(jù)集的 Venice-1102(右)的收斂圖。圖 1 顯示了針對(duì)這些問題的 3D 地標(biāo)和相機(jī)姿勢(shì)的可視化。虛線對(duì)應(yīng)于公差 τ ∈ {0.1, 0.01, 0.003, 0.001} 的成本閾值
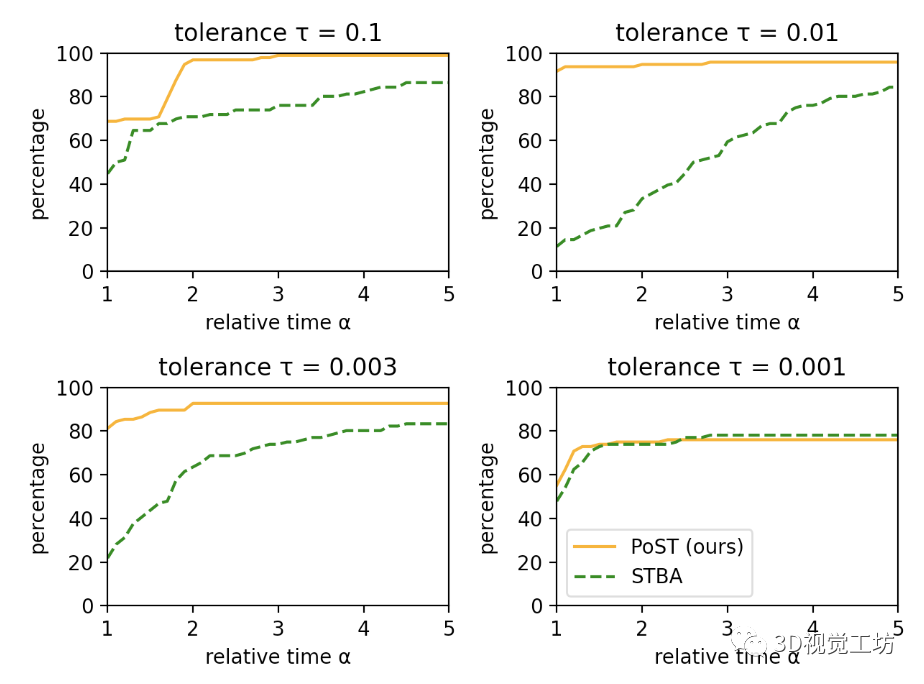
圖 7. 使用隨機(jī)框架的所有 BAL 問題的性能概況。我們提出的求解器 PoST 在所有精度公差 τ ∈ {0.1, 0.01, 0.003} 方面都優(yōu)于具有挑戰(zhàn)性的 STBA,無(wú)論是在速度還是精度方面,并且在 τ = 0.001 時(shí)與 STBA 相媲美
數(shù)據(jù)集
為了進(jìn)行廣泛的評(píng)估,我們使用了BAL項(xiàng)目頁(yè)面上的所有97個(gè)boundle adjustment問題。它們被分成五個(gè)問題家族。瓢蟲是由以正常速度行駛的車輛拍攝的圖像組成的。威尼斯、特拉法爾加和杜布羅夫尼克的圖像來(lái)自Flickr.com,并被保存為骨骼集[1]。用額外的樹葉圖像重組這些問題導(dǎo)致了菲納爾家族。關(guān)于這些問題的詳細(xì)信息可以在附錄中找到
LM循環(huán)
PoBA 符合實(shí)施 [4] 和 Ceres。從阻尼參數(shù) 10?4 開始,我們根據(jù) LM 循環(huán)的成功或失敗更新 λ。我們將 LM 迭代的最大次數(shù)設(shè)置為 50,如果達(dá)到 10?6 的相對(duì)函數(shù)公差,則提前終止。關(guān)于(23)和(32),我們將最大內(nèi)部迭代次數(shù)設(shè)置為 20,閾值 = 0.01。Ceres 和√BA 對(duì)內(nèi)部 CG 循環(huán)使用相同的強(qiáng)制序列,其中最大迭代次數(shù)設(shè)置為 500。
5.2.分析
圖 3 顯示了具有公差 τ ∈ {0.1, 0.01, 0.003, 0.001} 的所有 BAL 數(shù)據(jù)集的性能概況。對(duì)于 τ = 0.1 和 τ = 0.01,PoBA-64 在運(yùn)行時(shí)間和準(zhǔn)確性方面明顯優(yōu)于所有挑戰(zhàn)者。在高相對(duì)時(shí)間 α = 4 之前,PoBA-64 顯然仍然是出色精度 τ = 0.003 的最佳求解器。對(duì)于更高的相對(duì)時(shí)間,它與 √BA ? 32 具有競(jìng)爭(zhēng)力,并且仍然優(yōu)于所有其他挑戰(zhàn)者。從兩個(gè)不同大小的 BAL 問題的收斂圖中可以得出相同的結(jié)論(見圖 6)。圖 4 突出顯示了 PoBA 相對(duì)于所有 BAL 問題的挑戰(zhàn)者的低內(nèi)存消耗。無(wú)論問題的大小如何,PoBA 的內(nèi)存消耗都比√BA 和 Ceres 少得多。值得注意的是,它需要的內(nèi)存比√BA 少近五倍,比 Ceres-implicit 和 Ceres-explicit 少幾乎兩倍的內(nèi)存
5.3.power 隨機(jī)BA (PoST)
隨機(jī)BA。
STBA 將簡(jiǎn)化的相機(jī)系統(tǒng)分解為 Levenberg-Marquardt 迭代內(nèi)的集群。由于相機(jī)集群內(nèi)部的密集連接,每個(gè)集群的線性子問題然后與密集 LL》 分解并行解決。如 [22] 所示,這種方法在運(yùn)行時(shí)和擴(kuò)展到非常大的 BA 問題方面優(yōu)于基線,它甚至可以用于分布式優(yōu)化。在下文中,我們展示了用我們的 Power Bundle Adjustment 替換子問題求解器可以進(jìn)一步顯著提高運(yùn)行時(shí)間
power 隨機(jī)BA (PoST)
我們通過結(jié)合我們的求解器而不是密集的 LL》 分解來(lái)擴(kuò)展 STBA2。然后使用與第 5.1 節(jié)中相同的參數(shù)對(duì)逆 Schur 補(bǔ)碼進(jìn)行冪級(jí)數(shù)展開來(lái)求解每個(gè)子問題。根據(jù) [22],我們將最大簇大小設(shè)置為 100,并在 C++ 中用 double 編寫實(shí)現(xiàn)
分析
圖 7 顯示了針對(duì)不同公差 τ 的所有 BAL 問題的性能配置文件。對(duì)于 τ = 0.001,兩種求解器都具有相似的精度。對(duì)于 τ ∈ {0.1, 0.01, 0.003},PoST 在運(yùn)行時(shí)間和準(zhǔn)確性方面明顯優(yōu)于 STBA,尤其是 τ = 0.01。當(dāng)我們繪制不同大小的 BAL 問題的收斂曲線時(shí),會(huì)進(jìn)行相同的觀察(見圖 8)
六,結(jié)論
我們引入了一類新的大規(guī)模BA求解器,它利用逆 Schur 補(bǔ)碼的冪展開。我們證明了所提出的近似的理論有效性和該求解器的收斂性。此外,我們通過實(shí)驗(yàn)證實(shí),所提出的逆 Schur 補(bǔ)數(shù)的冪級(jí)數(shù)表示在速度、準(zhǔn)確性和內(nèi)存消耗方面優(yōu)于競(jìng)爭(zhēng)迭代求解器。最后但同樣重要的是,我們證明了冪級(jí)數(shù)表示可以補(bǔ)充分布式BA方法,以顯著提高其在大規(guī)模 3D 重建中的性能。
審核編輯 :李倩
-
3D
+關(guān)注
關(guān)注
9文章
2960瀏覽量
110913 -
矩陣
+關(guān)注
關(guān)注
1文章
434瀏覽量
35280 -
計(jì)算機(jī)視覺
+關(guān)注
關(guān)注
9文章
1709瀏覽量
46819
原文標(biāo)題:大規(guī)模 3D 重建的Power Bundle Adjustment
文章出處:【微信號(hào):3D視覺工坊,微信公眾號(hào):3D視覺工坊】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
3D打印能用哪些材質(zhì)?

3D視覺引領(lǐng)工業(yè)變革
基于樹莓派的工業(yè)級(jí) 3D 打印機(jī)!

3D IC背后的驅(qū)動(dòng)因素有哪些?

對(duì)于結(jié)構(gòu)光測(cè)量、3D視覺的應(yīng)用,使用100%offset的lightcrafter是否能用于點(diǎn)云生成的應(yīng)用?
運(yùn)行LCr4500 3d程序時(shí)報(bào)錯(cuò)怎么解決?
英倫科技裸眼3D便攜屏有哪些特點(diǎn)?

SciChart 3D for WPF圖表庫(kù)
騰訊混元3D AI創(chuàng)作引擎正式發(fā)布
騰訊混元3D AI創(chuàng)作引擎正式上線
3D打印技術(shù),推動(dòng)手板打樣從概念到成品的高效轉(zhuǎn)化

安寶特產(chǎn)品 安寶特3D Analyzer:智能的3D CAD高級(jí)分析工具



















評(píng)論