作者：Smita Choudhury 和 Abhilasha Kawle

在CTSD精密ADC系列文章的第3部分中，我們將重點介紹CTSD ADC的無混疊特性，無需添加任何外設設計即可提高對干擾源的抗擾度。第1部分展示了一類基于連續時間Σ-Δ（CTSD）架構的新型易于使用的無混疊精密ADC，可提供簡單、緊湊的信號鏈解決方案。第 2 部分為信號鏈設計人員揭開了 CTSD 技術的神秘面紗。本文比較了目前可用的精密ADC架構的混疊抑制解決方案背后的設計復雜性。我們將舉例說明一個理論來解釋CTSD ADC架構的固有混疊抑制。我們還展示了如何簡化信號鏈設計，并討論了CTSD ADC的擴展優勢。最后，我們將引入新的測量和性能參數來量化混疊抑制。

在聲納陣列、加速度計、振動分析等許多應用中，觀察到目標信號帶寬之外的信號，稱為干擾源。信號鏈設計人員面臨的主要挑戰是，ADC采樣現象會導致這些干擾源混疊到目標信號帶寬（帶內）并降低性能。除此之外，在聲納等應用中，帶內混疊的干擾源可能會被誤解為輸入信號，從而導致聲納周圍物體的誤測。抑制這些混疊的解決方案是傳統ADC信號鏈設計相當復雜的原因之一。CTSD ADC獨特的固有混疊抑制特性提供了一種新的簡化解決方案。在得出這個突破性的解決方案之前，本文的第一站是了解混疊的概念。

重溫奈奎斯特抽樣定理

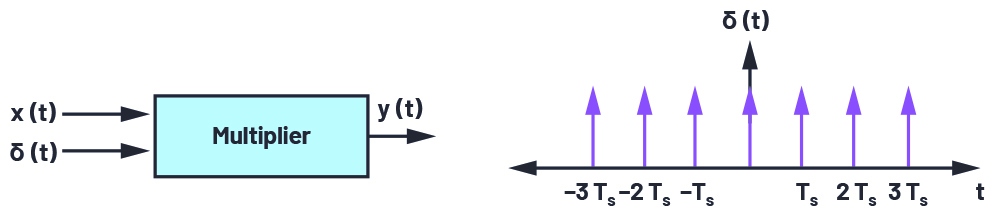
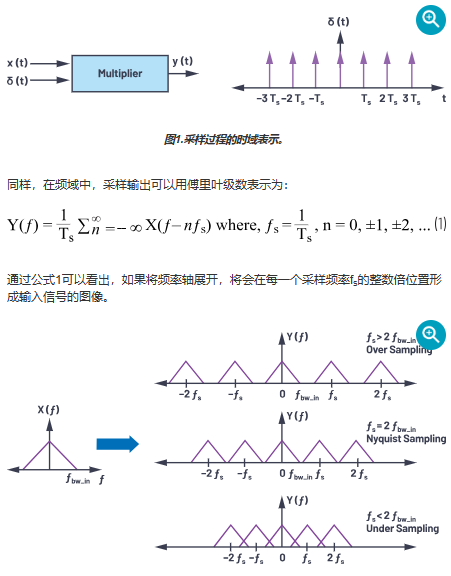
為了理解混疊的概念，讓我們快速回顧一下奈奎斯特采樣定理。可以在時域或頻域中分析信號。在時域中，模擬信號的采樣在數學上表示為信號的乘法——例如，x（t）與脈沖序列，δ（t），具有時間段Ts.

圖1.采樣過程的時域表示。

等效地在頻域中，采樣輸出可以使用傅里葉級數表示為：

公式1的意思很簡單，如果頻率軸展開，輸入信號的圖像在采樣頻率f的每個整數倍處形成s.

圖2.X（f） 通過不同采樣頻率采樣后的表示。

公式1表明X（f）在頻率f = n × f時的信號含量s， G在，其中 n = 0， ±1， ±2， ... ...， 將在 f 處表現出來在采樣后，類似于圖2中的欠采樣場景，說明了各種條件下的采樣現象。

圖3.（a）應用采樣定理來理解混疊，（b）使用抗混疊濾波器來衰減混疊頻率。

總之，奈奎斯特定理指出，任何大于采樣頻率一半的信號都會折疊或鏡像回小于fs/2，并且可能落入感興趣的頻帶。

假設ADC以頻率f采樣s并且系統中有兩個帶外音/干擾源，f1和 f2在ADC輸入端，如圖3所示。應用奈奎斯特定理，我們可以推斷，由于音調的頻率f。1小于 fs/2，采樣后，其頻率保持不變。雖然音調的頻率f2大于 fs/2，它將在感興趣的頻帶 f 中混疊自身bw_in，并降低該區域ADC的性能，如圖3a所示。

該理論也可以擴展到f以外的任何噪聲。s/2，它也會折返并在帶內表現出來，以增加帶內本底噪聲并降低性能。

混疊的現有解決方案

避免由于帶外 （OOB） 音調或噪聲折返而導致性能下降的簡單解決方案是衰減超出 f 的任何信號內容sADC使用低通濾波器（稱為抗混疊濾波器（AAF））進行采樣之前/2。圖3b顯示了簡單AAF的傳遞函數，并說明了頻率f下的衰減到混疊音2在它折回帶內之前。該AAF的主要特性是濾波器的階數和–3 dB轉折頻率。它們由通帶平坦度、特定頻率（如采樣頻率）所需的絕對衰減以及超出輸入帶寬（也稱為過渡帶）所需的衰減斜率決定。一些常見的濾波器架構是Butterworth、Chebhesev、Bessel和Sallen-Key，可以使用無源RC和運算放大器來實現。濾波器設計工具可幫助信號鏈設計人員針對給定的架構和要求進行 AAF 設計。

讓我們以一個示例應用程序來了解抗混疊濾波器的要求。在潛艇系統中，聲納傳感器發射聲波并分析水下的回波，以估計周圍物體的位置和距離。傳感器的輸入帶寬為100 kHz，系統檢測ADC輸入端任何>–85 dB音階的音調作為有效的回聲源。因此，來自帶外的任何干擾都需要由ADC衰減至少–85 dB，以避免被聲納系統檢測為輸入。針對這些要求，在下一節中，我們將構建并比較不同ADC架構的別名抑制解決方案。

在逐次逼近寄存器（SAR）和離散時間Σ-Δ（DTSD）ADC等傳統ADC架構中，采樣電路位于ADC的模擬輸入端，表明在ADC輸入之前需要AAF，如圖3b所示。

AAF 對 SAR/奈奎斯特采樣 ADC 的要求

SAR ADC的采樣頻率通常設置為模擬輸入頻率的兩倍或四倍（f在).這種ADC的AAF需要具有超出頻率f的窄過渡帶在，這意味著需要一個非常高階的濾波器。從圖4可以看出，采樣頻率約為1 MHz的SAR ADC需要一個五階巴特沃茲濾波器，以便在頻率大于100 kHz時獲得–85 dB抑制。在濾波器實現方面，隨著濾波器階數的增加，所需的無源器件和運算放大器數量也會增加。這意味著SAR ADC的AAF在信號鏈設計中需要大量的功耗和面積預算。

AAF 對 DTSD ADC 的要求

Σ-Δ型ADC是過采樣ADC，其采樣遠高于模擬輸入頻率。AAF 設計要考慮的混疊區域為 fs± f在.濾波器的過渡帶要求從f在到非常高的Fs.與 SAR ADC AAF 相比，這是一個更寬的過渡帶，表明所需的 AAF 階數也較低。圖4顯示，對于6 MHz采樣頻率DTSD ADC，對于f左右的頻率，要獲得–85 dB抑制。s– 100 kHz，通常需要二階 AAF。

在實際場景中，干擾源或噪聲可能位于頻帶中的任何位置，而不限于采樣頻率f附近s.任何小于 f 的頻率音調s/2，類似于頻率f的音調1在圖3中，不會表現為帶內以降低ADC性能。雖然 AAF 可能會衰減音調 f1在某種程度上，它仍然存在于ADC輸出中，是必須由外部數字控制器處理的不必要的信息。是否可以進一步衰減此音調，使其在ADC輸出端看不到？一種解決方案是使用具有超出頻率f的窄過渡帶的AAF在，但隨后濾波器設計的復雜性會增加。替代解決方案是片內數字濾波器，它是Σ-Δ調制器環路的一部分。

圖4.AAF 與 ADC 架構的復雜性與目標頻段的復雜程度。

圖5.DTSD ADC的STF，前端為AAF，后端為數字濾波器。

Σ-Δ調制器環路的數字濾波器

在Σ-Δ型ADC中，由于過采樣和噪聲整形，調制器輸出包含大量冗余信息，因此需要外部數字控制器進行大量處理。如果對調制器數據進行平均、濾波并以較低的輸出數據速率（ODR）提供，則可以避免這種冗余信息處理，ODR通常為2 × f在.抽取濾波器用于將采樣率從fs到所需的較低 ODR。使用數字濾波器的采樣速率轉換將在以后的文章中進行解釋，但這里的關鍵點是分立時間Σ-Δ調制器通常與片內數字濾波器配合使用。干擾源的組合信號傳遞函數（TF）與調制器前端的模擬濾波器和后端的數字濾波器如圖5所示。

總之，DTSD ADC 的 AAF 是基于混疊區域 f 周圍音調所需的衰減而設計的s.以及非鋸齒區域中的音調，例如 f1被片內數字濾波器完全衰減。

后端數字濾波器與前端模擬濾波器

SAR ADC在AAF中需要窄過渡帶，而Σ-Δ型ADC在數字濾波器中需要窄過渡帶。數字濾波器功耗低，易于集成在片上。此外，數字濾波器的階數、帶寬和過渡帶的編程比模擬濾波器簡單得多。

過采樣的優勢在于，它允許在后端使用寬轉換模擬濾波器和窄轉換數字濾波器，從而在功率、空間和抗干擾源方面提供優化的解決方案。

使用DTSD ADC時，AAF要求雖然放寬，但增加了設計復雜性，以滿足每次采樣事件后的建立時間要求，從而避免信號鏈性能下降。信號鏈設計人員面臨的挑戰是微調AAF，以在混疊抑制和輸出建立要求之間取得平衡。

新型精密CTSD ADC無需前端模擬濾波器設計，簡化了信號鏈設計。

CTSD ADC的固有別名抑制

在本系列的第2部分中，由閉環電阻反相放大器構建了一階CTSD調制器，如圖6所示。CTSD調制器遵循與DTSD調制器相同的過采樣和噪聲整形概念，以實現所需的性能，并且具有阻性輸入而不是開關電容輸入。調制器構建模塊包括一個連續時間積分器，后接一個對積分器輸出進行采樣和數字化的量化器，以及一個在輸入端閉合環路的反饋DAC。量化器輸入端的任何噪聲都是由積分器的增益傳遞函數形成的噪聲。

圖6.（a） CTSD調制器環路的構建模塊和（b）用于數學分析的簡化模塊表示。

擴展第 2 部分的信息，可以使用以下數學模型繪制 CTSD 調制器環路的簡化塊表示：

積分傳遞函數概括為H（f），也稱為環路濾波器。對于一階積分器，H（f） = 1/2πRC 。

ADC的功能是采樣和量化。因此，用于分析的簡化ADC模型使用采樣器，然后使用加性量化噪聲源。

DAC是一個模塊，它將當前時鐘周期中的輸入乘以一個常數。因此，它是一個具有脈沖響應的塊，在采樣時鐘周期內恒定，其余時間為 0。

這些簡化模型的等效框圖如圖6b所示，廣泛用于Σ-Δ性能分析。來自 V 的傳遞函數在到 V外稱為信號TF（STF）和Qe輸出稱為噪聲TF（NTF）。

關于CTSD調制器環路固有的混疊抑制特性，一種合理的解釋是，采樣不是直接發生在調制器的輸入端，而是在環路濾波器H（f）之后發生，如圖6a所示。但是為了獲得完整的圖片，將使用沒有采樣器的線性模型來理解概念，并且分析將擴展到與采樣器循環。

第 1 步：使用線性模型進行 STF 和 NTF 分析

為了簡化分析，忽略采樣器，線性模型如圖7所示。此循環的 STF 和 NTF 可以表示為

根據公式3，STF可以改寫為：

感興趣的頻率帶寬是低頻，因此在數學上它可以表示為f→0，而高頻可以表示為f→∞。繪制時，STF 和 NTF 的幅度（以 dB 為單位）與頻率的函數關系如圖 7 所示。

圖7.（a） 用于簡化分析的線性模型和 （b） STF（f） = H（f） × NTF（f）。

圖8.（a） 輸入 = 0 V 的 CTSD 調制器環路圖和 （b） 調制器環路的 NTF。

圖9.調制器環路的重新排列，以說明固有的混疊抑制。

NTF 類似于高通濾波器，STF 類似于低通濾波器，目標頻段的幅度為平坦的 0 dB，較高頻率的衰減相當于 AAF TF。在數學上，信號通過具有高增益、低通濾波器配置文件的H（f），然后由NTF環路處理。現在，通過首先了解NTF塊表示，可以將這種理解擴展到與采樣器一起循環。

步驟 2：NTF 的框圖表示

帶輸入 V在設置為0 V，調制器環路的框圖可以如圖8a所示重新排列，并用于NTF表示。當采樣器處于循環中時，NTF 響應將類似于線性模型，但每 f 的倍數處都有復制的圖像s，如圖 8b 所示。

第 3 步：重新排列調制器環路以可視化前期濾波動作

如果將環路濾波器H（f）和調制器環路的采樣器移至輸入端，并且反饋如圖9所示，則從輸入到輸出的傳遞函數沒有變化。此重新排列的框圖的右側表示 NTF。

與步驟1中的線性模型類似，在采樣等效系統中，輸入信號遍歷高增益H（f），然后通過NTF環路進行采樣和處理。信號通過環路濾波器的橫向在采樣之前會創建一個低通濾波器配置文件。該配置文件導致CTSD調制器的固有混疊抑制。因此，CTSD調制器環路的STF如圖9所示。

第 4 步：使用數字濾波器完成 STF

為了減少冗余高頻信息，CTSD調制器與片內數字抽取濾波器配合使用，組合混疊抑制TF如圖10所示。來自 f 周圍的別名s由CTSD固有的混疊抑制特性衰減，而中間干擾源則由數字濾波器衰減。

圖4比較了SAR ADC、DTSD ADC和CTSD ADC在采樣頻率下–80 dB抑制所需的AAF階數與輸入信號帶寬。帶有SAR ADC的AAF的階次和復雜性最高，而CTSD ADC不需要外部AAF，因為混疊抑制是其設計固有的。

CTSD架構帶來的信號鏈優勢

在某些多通道應用中，如聲納波束成形和振動分析，通道之間的相位信息非常重要。例如，通道之間的相位需要精確匹配，要求在20 kHz時為0.05°。

對于傳統的ADC信號鏈，AAF采用無源RC和運算放大器設計。濾波器在帶內引起一定的幅度和相位下降，這是轉折頻率的函數。為了獲得良好的通道間相位匹配，所有通道都需要具有相同的下降，這表明需要精細控制和匹配每個通道的濾波器轉折頻率。二階巴特沃茲濾波器，設計用于在16 MHz（采樣頻率）和f頻率下實現–80 dB抑制3分貝160 kHz（輸入帶寬）的相位失配在20 kHz時可能具有±0.15°，RC絕對值的誤差容限低至1%。容錯性較低的RC無源器件的可用性受到限制，并增加了物料清單（BOM）。

由于 AAF 在 CTSD ADC 信號鏈中被消除，因此通道間幅度和相位匹配本質上是在目標頻段內實現的。相位失配受到模擬調制器環路設計的片內失配的限制，在20 kHz時可能低至±0.02°。

圖 10.帶有后端數字濾波器的CTSD調制器環路。

測量和量化固有的別名拒絕

AD4134的ADC數據手冊中介紹了用于測量別名抑制的新功能檢查，AD4134是一款基于CTSD ADC架構的精密ADC。對ADC的模擬輸入信號的頻率進行掃描，并通過測量測試頻率折回的音調幅度（如果有的話）相對于所施加音調的幅度來計算每個帶外輸入信號的影響。

圖11顯示了AD4134在性能帶寬為160 kHz、采樣頻率為24 MHz時帶外頻率下的混疊抑制。對于 23.84 MHz （fs– 160 kHz），混疊抑制為 –85 dB，這是 ADC 的混疊抑制規格。還可以觀察到，對于其他中頻，抑制優于–100 dB。有關固有混疊抑制以及進一步提高這種抑制的選項的更多詳細信息，請參見AD4134數據手冊。

圖 11.混疊抑制與帶外頻率的關系。

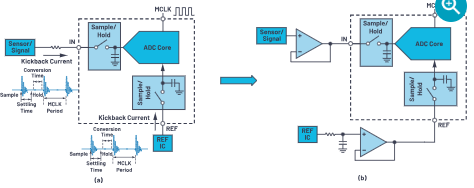
到目前為止介紹的CTSD ADC概念可以幫助信號鏈設計人員設想該架構的阻性輸入、阻性基準電壓源和固有混疊抑制的獨特特性。易于驅動的輸入和基準電壓源，加上CTSD ADC信號鏈的AAF設計，為各種應用帶來了新的簡化ADC前端設計。

審核編輯：郭婷