在結構光三維重建中,最常見的方法就是相移法,相移是通過投影一系列相移光柵圖像編碼,從而得到物體表面一點在投影儀圖片上的相對位置或者絕對位置。下面,筆者將詳細介紹如何制作相移編碼圖片,以及如何對獲取的相移圖片進行解碼,最后筆將粗淺的談談相移相比其他方法(如格雷碼)有什么優勢。
常見的三步相移法公式如下所示:
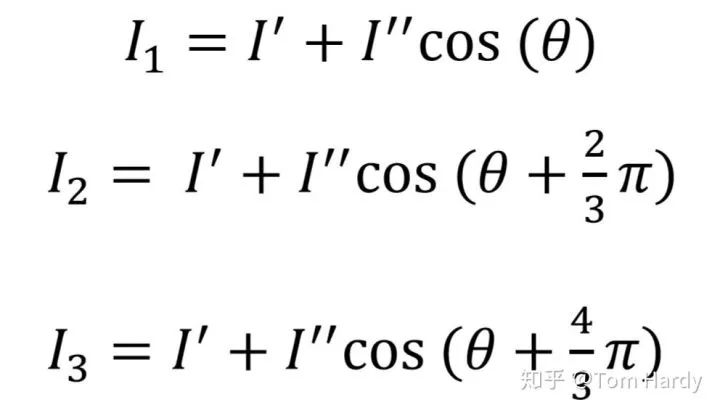
其中 I1,I2,I3是相位圖的灰度值,?是條紋光強的背景值,?
?為條紋光強的調制強度,?
?是相位主值。由于cos的取值范圍是[-1,1],在制作編碼圖片的時候,我們可以把?
?和?
都設置成127,這樣就可以保證制作的相位圖片的灰度值在0-255之間,以及一個高動態的范圍。實際上由于投影儀投射出來的光的灰度值并不是線性變化的,為了消除這種非線性變化問題,有不少人提出了各種針對投影光的伽馬矯正方法。如果精度要求不是特別嚴苛的話,投影儀投影的光在某個動態區間(通常是中間灰度值那一段,比如50-200的區間)會逼近于線性變化,我們也可以在制作圖片的時候把動態區間調整至逼近線性變換區間的范圍來消除這種非線性變化的干擾。
如下圖所示,是用三步相移公式做的相移圖片,為了更加清楚地描述,這里使用的是0-55的灰度值范圍。

三步相移法示例圖片
由之前我們知道,編碼主要是為了標記投影儀的圖片的實際位置,在相移中,我們用相位主值 編碼投影儀圖片的像素,對于某一個周期內的投影坐標,我們可以這樣把相位主值換成其在周期內的實際坐標:
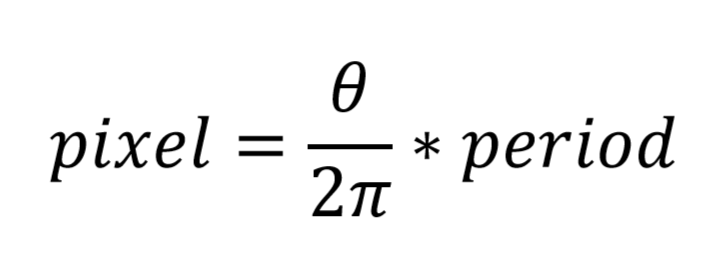
Pixel即該點在周期內的實際坐標,period即一個相位周期所占的像素列數,實際上,我們不可能僅用一個周期標記一整張相位圖片,其實很正常,我們的圖片列數常常是幾百甚至上千,而灰度值的動態范圍只有255, 所以我們通常會設計一個周期所占像素列數,如上圖所示,一個相位周期占圖片12列, 一張圖片約有10個周期。想要知道某個相位解碼點在投影圖片的實際坐標,我們除了知道其相位主值,還需要知道其是第幾個周期的相位。一個像素點的實際列坐標如下所示:
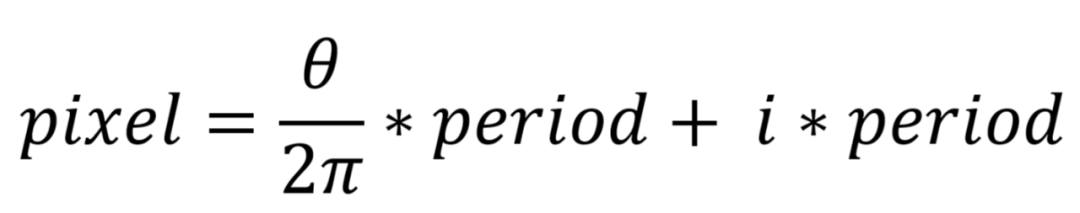
i 是相位所在的周期數(通常對第一個相位周期用0來編碼), i的數值常用格雷碼編碼或者其他編碼方法輔助得到。又可以根據相位展開后的主值在空域上的分布來求解其是第幾個周期,不過這樣通常不準。
把相移編碼光投影到物體表面后,我們就可以解碼了,如上面的方程所示,I1,I2,I3是相機圖片的灰度值,那么上述三個方程就只剩三個未知數,?三個方程解三個未知數在滿秩的情況下一定是可解的,而且對于這三個未知數來說,我們其實只需要關心 ,相位主值的大小。解碼公式如下所示:
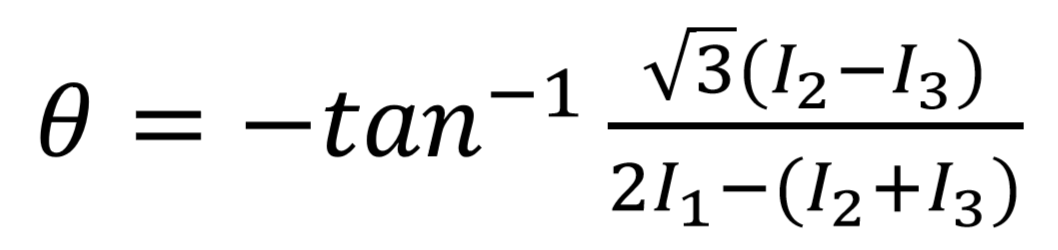
如果?解成?
?,則需要把其換算到?
?區間。上述相移編碼的解碼結果如下圖所示:

解碼后的相位主值圖
除了三步相移法,我們還可以設計四步甚至更多步相移法,具體編碼和解碼方式如下,對于N步相移法,我們需要N幅編碼圖片,對于第 ( )幅編碼圖片(通常我們用0標記第一幅圖片), 其編碼如下:

其對應的N步相移法的解碼公式為:
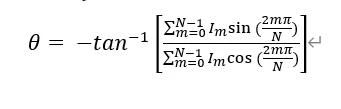
如何選定相移步長呢? 一般來說,步長越多越精確和穩定,但是在實際的應用中,考慮到三維成像幀率等原因,用三步或四步像移方法的較多。如果不考慮幀率的話,在論文[1]中有提到,如果能使用飽和式的相移圖片(saturated fringe patterns),即讓相移步長 N等于一個相位周期編碼列數的整數倍,如果編碼列數是偶數m的話,相移步長N可以是 m/2 的整數倍,這樣的話,解相移的時候對高反光表面相位主值也能解出比較好的結果。不過要對高反光表面的相移解碼得到非常好的效果,相移步長N通常都要在10以上,對于追求速度的三維重建,可能沒有那么吸引人。
最后,想和大家聊聊相移法比起格雷碼的優勢,首先,相移可以看成連續變化的值,比如說我們解相位換算成像素點坐標的時候,通常可以達到小數級(亞像素級)的精度,如果我們用格雷碼,在不使用插值的情況下,通常只能達到像素級的精度。為什么相移達到的亞像素級的精度是正確的呢?認為和光本身就是一種正弦波有關,光打在物體表面上,會以正弦波的形式向周邊散開,所以使用相移時得到的亞像素級的解碼精度往往是比較準確的。此外,我們用的相移是時序,利用光的在時間中(不同投影圖片下)的變化量來解碼,相比格雷碼用閾值二值化,受到物體紋理的影響會更小。比如相移光打在暗色物體上,可能解出來的 會比較小,但是不影響我們解出正確的相位主值 。
審核編輯:郭婷
-
投影儀
+關注
關注
4文章
891瀏覽量
44143 -
編碼
+關注
關注
6文章
969瀏覽量
55817
原文標題:系列篇|結構光三維重建——相移法基本原理
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
航天宏圖全棧式3DGS實景三維重建系統解決方案

激光三維掃描技術:無噴粉條件下高反光表面三維重建的光學原理與應用
VirtualLab:光學系統的三維可視化
奧比中光助力創想三維登頂世界消費級3D掃描儀市場
使用DLP LightCrafter4500投影結構光進行三維重建遇到的疑問求解
在結構光三維成像方面DLP LightCrafter 4500如何連續投射彩色圖?
三維測量在醫療領域的應用
三維測量技術在工業中的應用
商湯科技運用AI大模型實現實景三維重建
CASAIM與邁普醫學達成合作,三維掃描技術助力醫療輔具實現高精度三維建模和偏差比對
建筑物邊緣感知和邊緣融合的多視圖立體三維重建方法

混合鍵合的基本原理和優勢
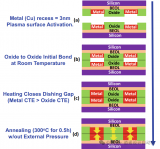
3DP工藝基本原理
留形科技借助NVIDIA平臺提供高效精確的三維重建解決方案
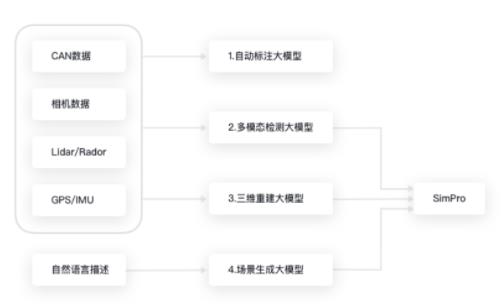
基于大模型的仿真系統研究一——三維重建大模型



















評論