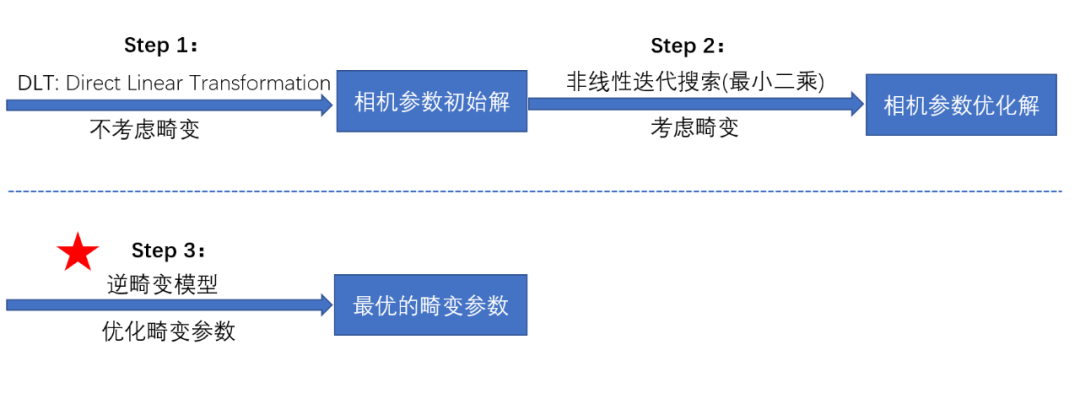
相機標定可以歸納為P?n?P(Perspective-n-Point)的問題，即已知三維物點坐標和對應的二維投影坐標，求解相機參數。由于鏡頭的畸變(徑向和切向)帶來非線性成像模型，一般求解方法分為兩步：

不考慮畸變，成像模型為線性模型，利用線性求解方法求出初始解

考慮畸變，利用初始解和成像模型對三維物點投影得到的投影點與觀測點形成最優問題， 通過最小二乘進行估計。

這篇文章的精彩之處在于給出逆畸變模型，在上兩步的基礎上，利用逆畸變模型進一步優化畸變參數。文章的主要框架內容：

1.相機模型

1.1正投影模型

1.2反投影模型

1.3需要標定的參數：

2.**圓形標定點的偏差校正**

3.逆畸變模型

3.1遞歸逆畸變模型

3.2非遞歸逆畸變模型:

4.利用逆畸變模型優化畸變系數

5.驗證逆畸變模型的精度

參考文獻：

1.相機模型

1.1正投影模型

相機的內參：

相機的外參：

相機的畸變模型：

1.2反投影模型

1.3需要標定的參數：

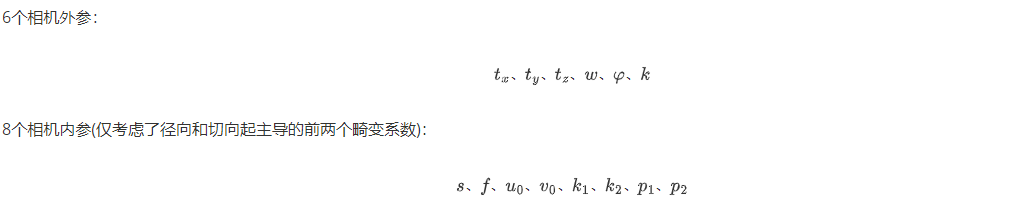
2.圓形標定點的偏差校正

透視投影不是保形變換，直線在透視投影模型下為直線，一般二維或三維形狀與圖像平面不共面時會發生變形。常用的標定板是棋盤格，棋盤格的角點是包型變換，但不易精準檢測。圓形標定板也是校準中常用的標志板，圓形可以準確的找到中心點，但通過透視投影圓心會發生偏差。

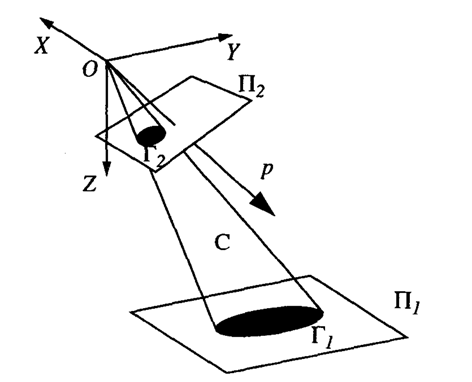
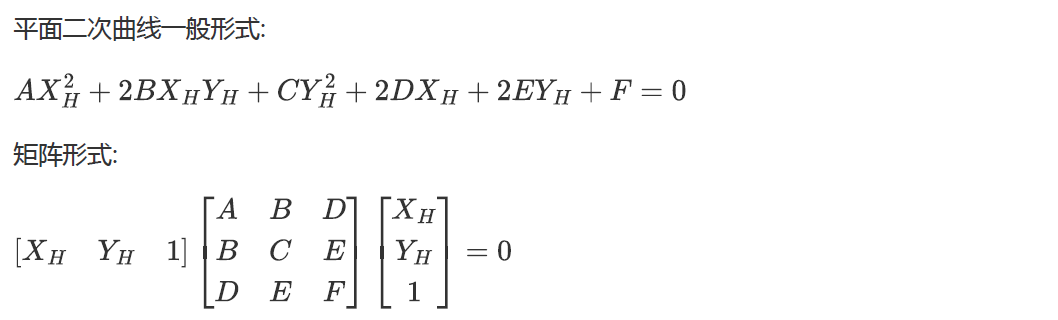
令：

則圓的表示形式：

得：

因為反相機模型：

3.逆畸變模型

畸變矯正：

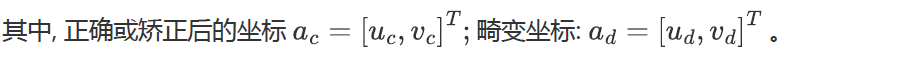
3.1遞歸逆畸變模型

由(4)可得:

3.2非遞歸逆畸變模型:

4.利用逆畸變模型優化畸變系數

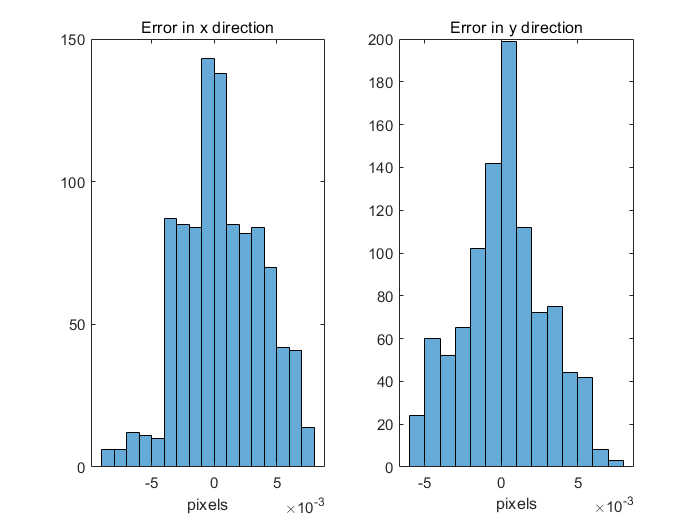
5.驗證逆畸變模型的精度

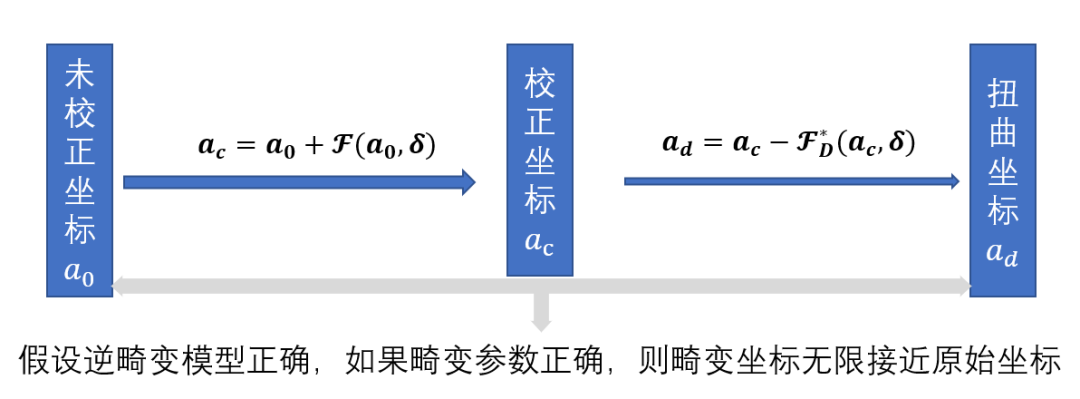
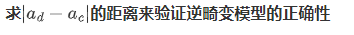
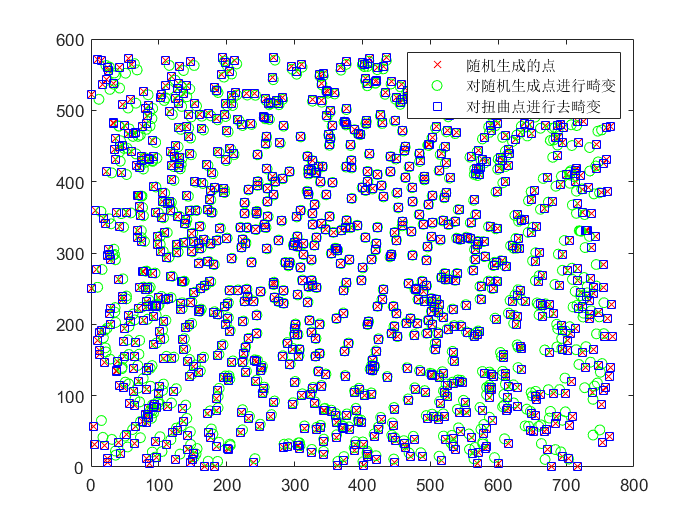
未矯正坐標和扭曲坐標之間的差異可用直方圖表示,表明誤差小于0.01像素。

審核編輯：郭婷