從事開關電源研發的工程師,尤其是模擬控制的電源設計師,比較熟悉連續時域、連續頻域的傳遞函數分析。那如何把模擬控制變成數字控制呢?因為計算機或者CPU它本質上是一個采樣系統,只能處理離散系統,所以要把連續域變換成離散域,并且離散域的方程才能成為差分方程的形式,也只有差分方程才好寫成C代碼控制。我們今天分享,如何把連續頻域變成離散域的其中一種變換方法:Tustin變換法(雙線性變換法),這也是實際研發中非常常用的一種變換方法。
我們開始舉例,已知連續校正環節傳遞函數D(s)為:
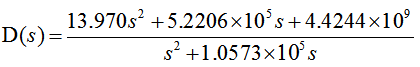
其中變換器的開關頻率為fs=250kHz。如何設計雙線性變換法所得的離散控制器D(z),并比較D(s)與D(z)的頻率特性呢?
1)先利用matlab把D(s)離散成D(z):
① Tustin變換法(雙線性變換法):
fs=250000;
T=1/fs;
Ds=tf([13.970 5.2206e5 4.4244e9],[1 1.0573e5 0]);
Dz=c2d(Ds,T,'tustin')
Transfer function:
12.41 z^2 - 23.03 z + 10.68
z^2 - 1.651 z + 0.6509
Sampling time: 4e-006
2)利用matlab繪制離散控制器D(z)的頻率特性,代碼如下:
T=4e-6;
w=0:1:4*pi/T;
f=w/2/pi;
num_d_s=[13.970 5.2206e5 4.4244e9];
den_d_s=[1 1.0753 0];
num_d_z=[12.41 -23.03 10.68];
den_d_z=[1 -1.651 0.6509];
[m_d_s,p_d_s]=bode(num_d_s,den_d_s,w);
[m_d_s,p_d_s]=bode(num_d_s,den_d_s,w);
[m_d_z,p_d_z]=dbode(num_d_z,den_d_z,T,w);
subplot(2,1,2),plot(f,p_d_s,'-',f,p_d_z,'-');
xlabel('Frequency(Hz)'),ylabel('phase(deg)');
axis([0 2/T -100 100]);
grid on;
subplot(2,1,1),plot(f,20log10(m_d_s),'-',f,20log10(m_d_z),'-'),title('BodeDiagrams');
xlabel('Frequency(Hz)'),ylabel('Magnitude(dB)');
axis([0 2/T 0 40]);
grid on;
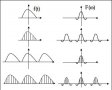
3)連續控制器D(s)與離散控制器D(z)的頻率特性如下圖1:
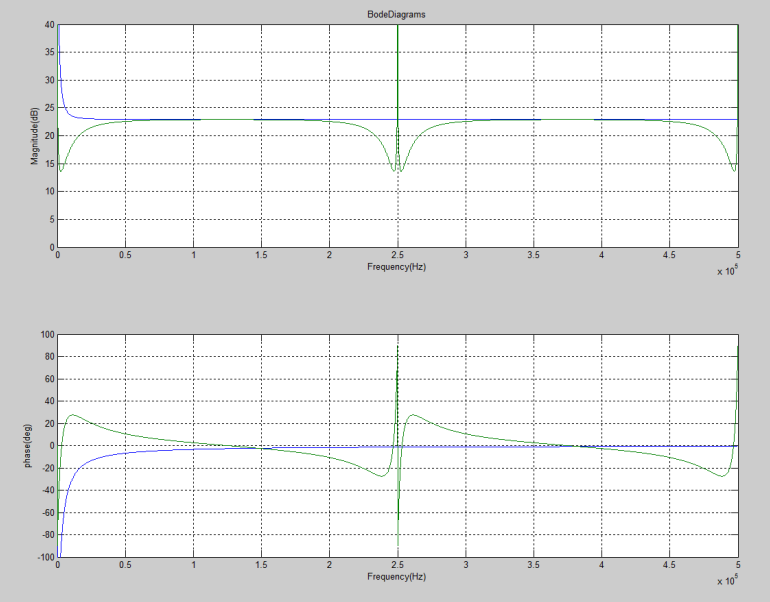
圖1 仿真圖
以上就是 Tustin變換法(雙線性變換法)的簡單過程,簡單的3個步驟,既可以得到連續域與離散域的仿真圖,是不是很簡單呢?另一個問題,數字控制還有其他變換方法嗎?有的,并且在實際產品開發中也比較常用,我們下次繼續分享。
-
電源
+關注
關注
184文章
17769瀏覽量
250739 -
開關電源
+關注
關注
6468文章
8351瀏覽量
482528 -
matlab
+關注
關注
185文章
2977瀏覽量
230645 -
控制器
+關注
關注
112文章
16396瀏覽量
178512 -
數字電源
+關注
關注
28文章
515瀏覽量
109330
發布評論請先 登錄
相關推薦




 數字電源中如何把連續頻域變換為離散域(一)
數字電源中如何把連續頻域變換為離散域(一)
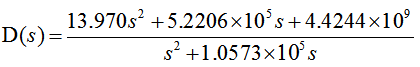
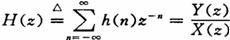
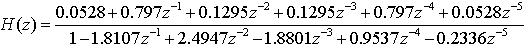










評論