
文章轉發自51CTO【ELT.ZIP】OpenHarmony啃論文俱樂部——《統計壓縮編碼機理分析》
上篇回顧:《統計壓縮編碼機理分析(上篇)》6.算術編碼
《上篇》中第五章的“哈夫曼編碼”方法建立在符號和碼字相對應的基礎上。若對信源單符號進行編碼,則符號間的相關性就無法考慮:若將 m 個符號合起來編碼,第一是會增加設備復雜度,第二是 m+1 個符號間以及組間符號的相關性還是無法考慮。這就使信源編碼的匹配原則不能充分滿足,編碼效率就有所折損。為了克服這種局限性,研究了非分組碼的編碼方法。
算術編碼是一種非分組碼,其基本原理是將編碼的消息表示成實數0和1之間的一個間隔,消息越長,編碼表示它的間隔就越小,表示這一間隔所需的二進制位就越多。
算數編碼是一種在有損壓縮與無損壓縮算法中都經常使用的一種算法,主要應用于圖像壓縮。算數編碼與其它統計編碼不同,其它的統計編碼通常是把輸入的消息分割成符號后對其進行編碼,而算數編碼則將輸入的字符劃分成若干個子區間來代表一個字符,計算其概率,進行編碼。
6.1基本機理
算術編碼的背后是深刻的數學思想,簡單來說,它做了這樣一件事情:
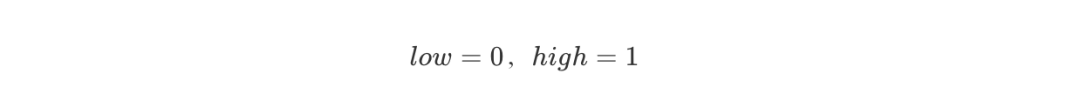
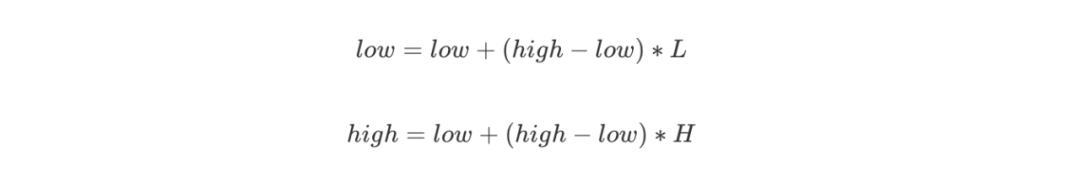
-
假設有一段數據需要編碼,統計里面所有的字符和出現的次數
-
將區間 [0,1) 連續劃分成多個子區間,每個子區間代表一個上述字符, 區間的大小正比于這個字符在文中出現的概率 p。概率越大,則區間越大。所有的子區間加起來正好是 [0,1)
-
編碼從一個初始區間 [0,1) 開始,設置:
-
不斷讀入原始數據的字符,找到這個字符所在的區間,例如 [ L, H ),更新:
-
最后將得到的區間 [low, high)中任意一個小數以二進制形式輸出即得到編碼的數據:
6.2編碼過程
給出下面一段十分簡單的原始數據:
ARBER
像所有統計編碼一樣,統計各字符出現的次數與概率:
| 字符 | 次數 | 概率 |
| A | 1 | 0.2 |
| B | 1 | 0.2 |
| E | 1 | 0.2 |
| R | 2 | 0.4 |
將這幾個字符的區間在 [0,1) 上按照概率大小連續一字排開,我們得到一個劃分好的 [0,1)區間:
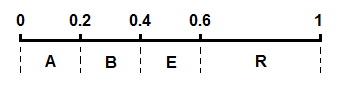
開始編碼,初始區間是 [0,1)。注意這里又用了區間這個詞,不過這個區間不同于上面代表各個字符的概率區間 [0,1)。這里我們可以稱之為編碼區間,這個區間是會變化的,確切來說是不斷變小。我們將編碼過程用下圖完整地表示出來:
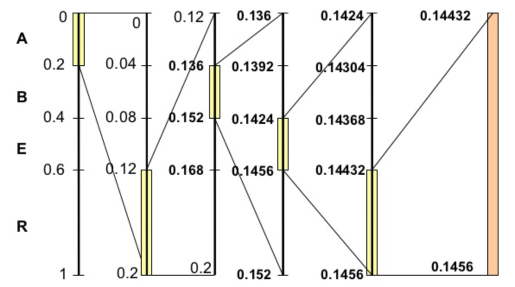
我們對其進行步驟拆解:
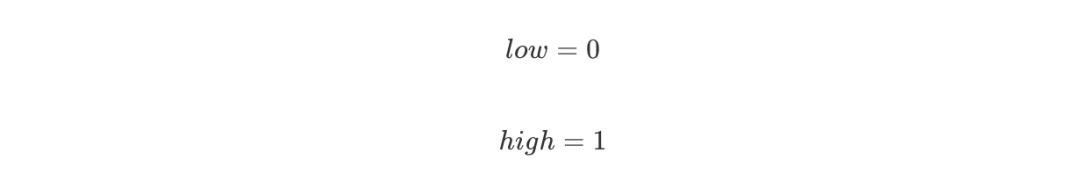
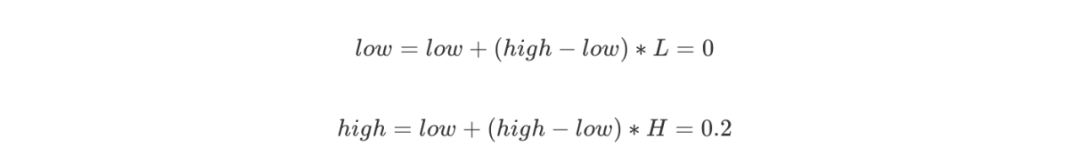
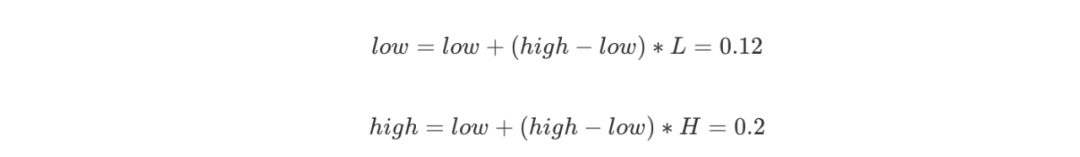
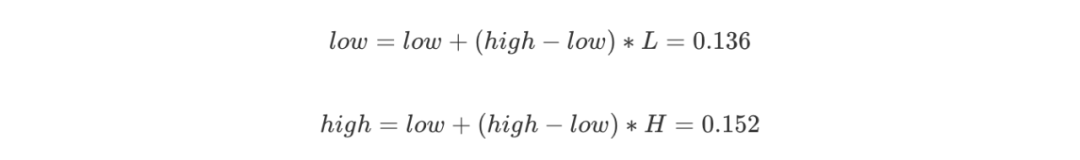
-
剛開始編碼區間是 [0,1),即:
-
第一個字符A的概率區間是 [0,0.2),則 L = 0,H = 0.2,更新:
-
第二個字符R的概率區間是 [0.6,1),則 L = 0.6,H = 1,更新:
-
第三個字符B的概率區間是 [0.2,0.4),則 L = 0.2,H = 0.4,更新:
我們可以看到一個不斷變化的小數編碼區間。每次編碼一個字符,就在現有的編碼區間上,按照概率比例取出這個字符對應的子區間。例如一開始A落在0到0.2上,因此編碼區間縮小為 [0,0.2),第二個字符是R,則在 [0,0.2)上按比例取出R對應的子區間 [0.12,0.2),以此類推。每次得到的新的區間都能精確無誤地確定當前字符,并且保留了之前所有字符的信息,因為新的編碼區間永遠是在之前的子區間。最后我們會得到一個長長的小數,這個小數即神奇地包含了所有的原始數據,不得不說這真是一種非常巧妙的思想。
6.3解碼過程
如果理解了編碼的原理,那么解碼的方法顯而易見,就是編碼過程的逆推。從編碼得到的小數開始,不斷地尋找小數落在了哪個概率區間,就能將原來的字符一個個地找出來。例如得到的小數是0.14432,則第一個字符顯然是A,因為它落在了 [0,0.2)上,接下來再看0.14432落在了 [0,0.2)區間的哪一個相對子區間,發現是 [0.6,1), 就能找到第二個字符是R,依此類推。在此不再贅述具體步驟。
6.4算法實現
char inStr[100], chSet[20]; //輸入字符串和字符集
float P[20]; //每個字符的概率
float pZone[20]; //概率區間
int strLen; //輸入字符串長度
int chNum; //字符集中字符個數
int binary[100];
float infoLen; //信息量大小
void compress(); //編碼函數
void uncompress(); //解碼函數
int main()
{
int i,j;
printf("input the length of char set:
");
scanf("%d", &chNum);
getchar();
printf("input the char and its p
");
for (i=0; i < chNum; i++) {
printf("input char: ");
scanf("%c", &chSet[i]);
getchar();
//printf("sssss%c ", chSet[i]);
printf("
input its p: ");
scanf("%f",&P[i]);
getchar();
printf("
");
}
/* test
for (i = 0; i < chNum; ++i)
printf("%c<-------------->%f
", chSet[i], P[i]);
*/
// 計算概率區間
pZone[0] = 0;
for (i=1; i < chNum; ++i)
pZone[i] = pZone[i-1] + P[i-1];
printf("input the string
");
fgets(inStr, 100, stdin);
strLen = strlen(inStr);
/************* test ***************/
printf("the string is:
");
puts(inStr);
printf("*********** compress **************
");
compress();
printf("
*********** uncompress **************
");
uncompress();
return 0;
}
void compress()
{
float low = 0, high = 1;
float L, H, zlen = 1;
float cp; //輸入字符的概率
float result; //結果
int i, j;
for (i=0; i < strLen; i++) {
for (j=0; j < chNum; j++) {
if (inStr[i] == chSet[j]) {
//cp = P[j];
//L = pZone[j];
low = low + zlen * pZone[j];
zlen *= P[j];
break;
}
}
//low = low + zlen * L;
//zlen *= cp;
}
result = low;
printf("the result is %f
", result);
infoLen = log(1/zlen) / log(2); //計算香農信息量
if(infoLen > (int)infoLen)
infoLen = (int)infoLen + 1;
else
infoLen = (int)infoLen;
for (i=0; i < infoLen; i++) {
result *= 2;
if (result > 1) {
result = result - 1;
binary[i] = 1;
} else if (result < 1) {
binary[i] = 0;
} else {
break;
}
}
if (i >= infoLen) {
for (j=i; j >= 1; j--) {
binary[j-1] = (binary[j-1]+1)%2;
if (binary[j-1] == 1)
break;
}
}
printf("****************** the compress result*****************
");
for (j=0; j < i; j++)
printf("%d ", binary[j]);
}
void uncompress()
{
int i,j;
float w = 0.5;
float deResult=0;
float newLow,newLen;
float low=0,zlen=1;
for (i=0; i < infoLen; i++) {
deResult += w*binary[i];
w *= 0.5;
}
printf("uncompress to ten:%f
", deResult);
printf("uncompress result:
");
for (i=0; i < strLen; i++) {
for (j=chNum; j > 0; j--) {
newLow = low;
newLen = zlen;
newLow += newLen * pZone[j-1];
newLen *= P[j-1];
if (deResult >= newLow) {
low=newLow;
zlen=newLen;
printf("%c ",chSet[j-1]);
break;
}
}
}
}
6.5與哈夫曼編碼的比較我們首先回顧一下哈夫曼編碼,換一組數據并統計字符的出現次數,生成哈夫曼樹,我們可以得到以下字符編碼集:| 字符 | 次數 | 編碼 |
| a | 3 | 0 |
| b | 3 | 1 |
| c | 2 | 10 |
| d | 1 | 110 |
| e | 2 | 111 |
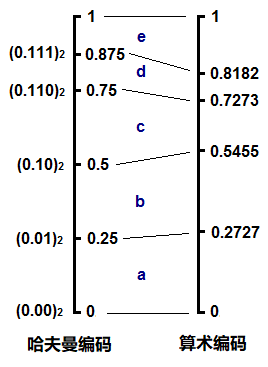
如果點上小數點,把它也看成一個小數,其實和算數編碼的形式很類似,不斷地讀入字符,找到它應該落在當前區間的哪一個子區間,整個編碼過程形成一個不斷收攏變小的區間。
由此我們可以看到這兩種編碼,或者說熵編碼的本質。概率越小的字符,用更多的bit去表示,這反映到概率區間上就是,概率小的字符所對應的區間也小,因此這個區間的上下邊際值的差值越小,為了唯一確定當前這個區間,則需要更多的數字去表示它。我們仍以十進制來說明,例如大區間0.2到0.3,我們需要0.2來確定,一位足以表示;但如果是小的區間0.11112到0.11113,則需要0.11112才能確定這個區間,編碼時就需要5位才能將這個字符確定。其實編碼一個字符需要的bit數就等于 -log ( p ),這里是十進制,所以log應以10為底,在二進制下以2為底,也就是香農公式里的形式。
哈夫曼編碼的不同之處就在于,它所劃分出來的子區間并不是嚴格按照概率的大小等比例劃分的。例如上面的d和e,概率其實是不同的,但卻得到了相同的子區間大小0.125;再例如c,和d,e構成的子樹,c應該比d,e的區間之和要小,但實際上它們是一樣的都是0.25。我們可以將哈夫曼編碼和算術編碼在這個例子里的概率區間做個對比:
7.數據壓縮的定義、背景與分類
首先我們要知道什么是數據壓縮。數據壓縮是指在不丟失有用信息的前提下,縮減數據量以減少儲存空間,提高其傳輸、儲存和處理效率,或按照一定的算法對數據重新組織,減少數據的冗余和存儲空間的一種技術方法。
那么為什么會出現數據壓縮這門技術呢?一門技術的快速發展必然有其背景,有其誕生的必要性。
數據壓縮背景摘要:在信息儲存和數據傳輸日益增長的今天,數據壓縮變得越來越重要,數據壓縮是一種用來減小數據大小的技術。當一些巨大的文件必須通過網絡傳輸存儲在數據存儲設備上,且其大小超過數據存儲的容量或將消耗大量的網絡傳輸帶寬時,這是非常有用的。隨互聯網和資源有限的移動設備的出現,數據壓縮變得更加重要。它可以有效地用于節省儲存空間和帶寬,從而減少了下載時間.
數據壓縮算法發展至今,已經有了相當多的算法,按數據質量可分為有損壓縮和無損壓縮兩大類。無損算法可以從壓縮的信息中精確地重構原始消息,有損算法只能近似地重構原始消息。
8.游程編碼(RLE)
設想一下,一旦一個像素呈現出一種特定的顏色(黑色或白色),下面的像素極有可能也是相同的顏色。因此,與其單獨編碼每個像素的顏色,我們可以簡單地編碼每個顏色的運行長度。RLE是一種非常簡單的數據壓縮形式,其中數據序列(稱為游程,重復的字符串)存儲在兩個部分:單個數值和計數。這對于包含許多這樣的運行的數據是最有用的,例如,簡單的圖形圖像,如圖標、線條圖和動畫。但它對于運行次數不多的文件是沒有用的,因為它可能會大大增加文件的大小。
例如:純白色背景上的純黑色文本,b 代表一個黑色像素,w 代表一個白色像素:wwwwwbwwwwwbbbwwwwwbwwwww 用RLE表示為:5w1b5w3b5w1b5w
由于游程編碼執行無損數據壓縮,它非常適合基于調色板的圖像,如紋理。但通常不應用于現實的圖像,如照片。另外,游程編碼用于傳真機非常高效,因為大多數傳真文件都有很多空白,偶爾會有黑色的干擾。
9.Lempel-Ziv算法
lempel-Ziv 算法是一種基于字典的編碼算法,而以往的算法往往基于概率編碼,它是文件無損壓縮的首選方法。這主要是由于它對不同文件格式的適應性但是對于小文件,字典的長度可能會超過原始文件的長度,但是對于大文件,這種方法是非常有效的。
Ziv 和 Lempel 在1977年和1978年的兩篇獨立論文中描述了該算法的兩個主要變體,通常被稱為 LZ77和 LZ78。
LZ77 算法基于滑動窗口的思想,該算法只在距離當前位置固定距離內的窗口查找匹配項。而 LZ78 算法基于一種更保守的方法向字典中添加字符串。
lempel-ziv-welch(LZW) 是目前使用最多的 Lempel-Ziv 算法。它是在 LZ77 和 LZ78 壓縮算法的基礎上改進的。編碼器建立一個自適應字典來表示變長字符串,不需要任何先驗概率信息。解碼器根據接收到的代碼動態地在編碼器中構建相同的字典。
現在 LZW 應用于 GIF 圖像,UNIX 壓縮等。
基本步驟:
-
初始化字典。
-
將輸入數據的符號按順序組合到緩沖區中,直到在字典中找到最長的字符串
-
在緩沖區中發送表示的代碼。
-
將緩沖區中的字符串與下一個空代碼中的下一個符號結合保存到字典中。
-
清空緩沖區,然后重復步驟 2~5,直到全部數據結束。
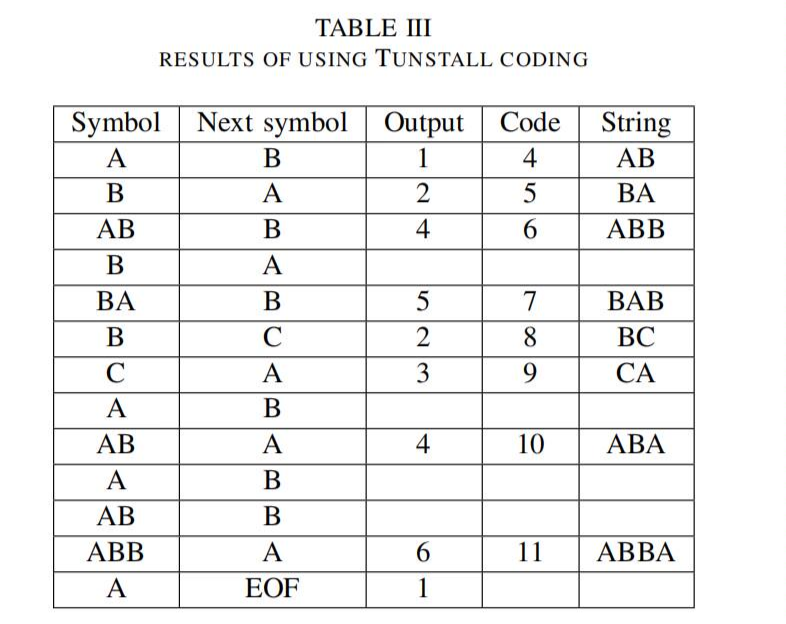
表3是一個LZW的例子,輸入字符串為ABABBABCABABBA,初始碼為1、2、3,分別表示A、B、C。
編碼后的字符串為“124523461”。14個字符壓縮為9個字符。因此壓縮比為14/9=1.56。
9.1LZ編碼的應用
在LZ的變體中,最流行的是LZW算法然而,LZW最初是實用最多的算法,專利問題導致越來越多的使用LZ算法。LZ算法最受歡迎的實現是Phil Katz最初設計的deflate算法。Deflate是一種無損數據壓縮算法,使用了LZ算法和哈夫曼算法的組合,下面列舉LZ算法的主要應用:
9.1.1文件壓縮 UNIX 壓縮
UNIX compress 命令是LZW最早的應用之一。字典的大小是自適應的。當字典被填滿時,大小逐漸增加一倍。代碼字的最大大小bmax可以由用戶設置為9到16之間,16位是默認值。而一旦字典包含2bmax條目,壓縮就會成為一種靜態字典編碼技術,此時算法監視壓縮比。如果壓縮比低于閾值,則將刷新字典,并重新啟動字典構建過程。這樣一來,字典總是能反映源的地方特征。
9.1.2圖像壓縮 gif 格式
圖形交換格式(GIF)是 Compuserve 信息服務公司開發的圖形圖像編碼格式。它是 LZW 算法的另一種實現,與 Unix 中的 compress 命令非常相似,正如我們在前面的應用程序中提到的那樣。
9.1.3圖像壓縮 png 格式
PNG 標準是互聯網上最早開發的標準之一。1994 年12 月,Unisys 公司(該公司從 Sperry 那里獲得了 LZW的專利)和 CompuServe 公司宣布,他們將開始向支持GIF 的軟件的作者收取版稅。該公告導致了數據壓縮領域的一場革命,行成了Usenet組comp.compression的核心。社區決定開發一種無專利的 GIF 替代品,三個月內 PNG 誕生了。Modem sV.42 上的壓縮ITU-T 建議 V.42 之二是為通過電話網絡使用而制定的壓縮標準,并附有 C CITT 建議 V.42 中所述的糾錯程序。該算法用于連接計算機和遠程用戶的調制解調器。該算法有兩種運行模式和壓縮模式。在透明模式下,數據以不壓縮的形式傳輸,在壓縮模式下,數據使用LZW算法進行壓縮。
10.多媒體壓縮JPEG和MPEG
10.1背景
媒體圖像已經成為日常生活中一個至關重要且無處不在的組成部分。圖像中編碼的信息量是相當大的。即使有了帶寬和儲存能力的進步,如果圖像不被壓縮,許多應用程序的成本將會太高。
10.2圖像壓縮:JPEG壓縮算法
JPEG用于靜態圖像,圖像壓縮是減少表示數字圖像所需的數據量的過程,這是通過刪除所有冗余或不必要的信息來實現的。一個未壓縮的圖像需要大量的數據來表示。
編碼算法:
1、顏色空間轉換
如果顏色分量是獨立的(不相關的),則可以獲得最好的 壓縮結果,例如在YCbCr中,大部分信息集中在亮度上,而色度上的信息較少。RGB顏色分量可以通過線性變換轉換為YCbCr分量,如下式:

2、色度下降采樣
使用YCbCr顏色空間,我們還可以通過壓縮Cb和Cr分量的分辨率來節省空間。它們是色度分量,我們可以減少它們以使用圖像壓縮。由于亮度對眼睛的重要性,我們不需要色度像亮度一樣頻繁,所以我們可以對其進行下降采樣。因此可以除去部分Cb和Cr的元素。因此,例如將RGB44格式轉換為YCbCr42的格式,這樣就可以獲得一個1:5的數據壓縮比,不過此步驟是一個可選的過程。
3、離散余弦變換(DCT)
在這一步,每88塊的分量(Y,Cb,Cr)被轉換成頻域表示。DCT方程是一個相當復雜的方程,有兩個余弦系數。細節參考JPEG標準。
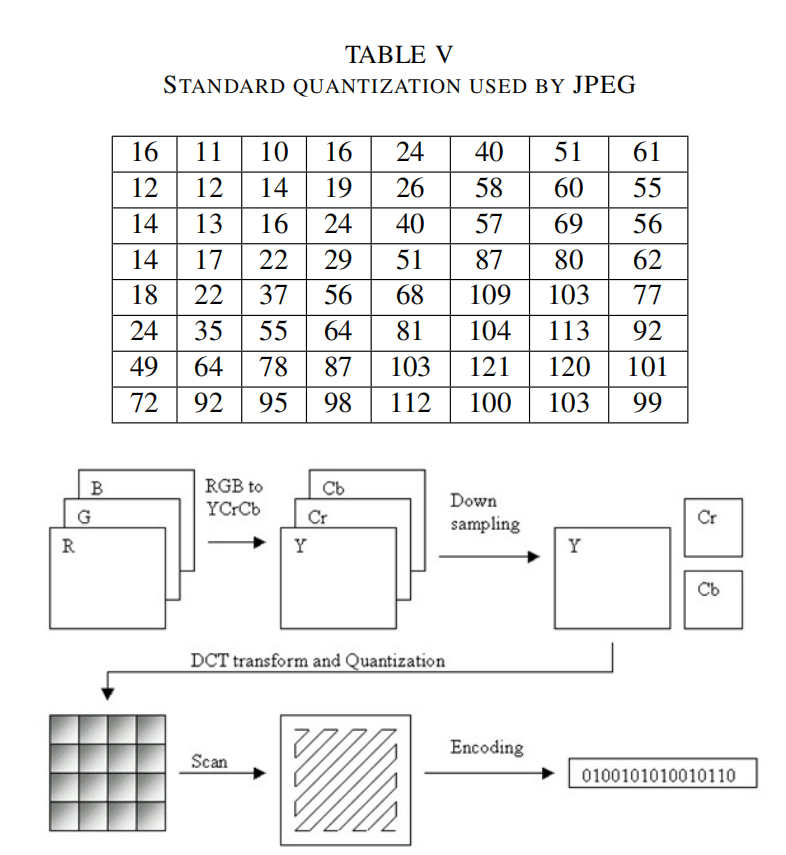
4、量化
對人眼來說,亮度比色度更重要。對眼睛來說,在大范圍內看到亮度的微小差異比高頻亮度變化的確切強度更容易分辨。利用這一特性,我們可以大大減少高頻成分中的信息。JPEG編碼通過簡單地將頻率域中的每個分量除以該分量中的一個常數,然后四舍五入到最近的整數來實現這一點。因此,許多高頻分量被四舍五入到零,其余大部分分量變成了小的正數或負數,占用更少的比特來儲存。
5、熵編碼
熵編碼是一種無損數據壓縮的方法。在這里,我們將圖像組件排序為鋸齒形,然后使用游程編碼(RLE)算法,將相似的頻率連接在一起,以壓縮序列。
6、哈夫曼算法
應用前面的步驟,我們得到的數據就是DCT系數序列。這一步即是最后一步,我們用哈夫曼編碼或者算數壓縮算法來壓縮這些系數。該方案主要采用Huffman壓縮,將其視為第二次無損壓縮。
10.3視頻壓縮:MPEG壓縮算法
MPEG壓縮算法的基本思想是將離散樣本流轉換為符號的比特流。以減少占用空間,理論上,視頻流是一組離散圖像。MPEG使用這種連續幀之間的特殊或時間關系來壓縮視頻流。在一段數據中,利用這些關系的技術越有效,對數據的壓縮就越有效。
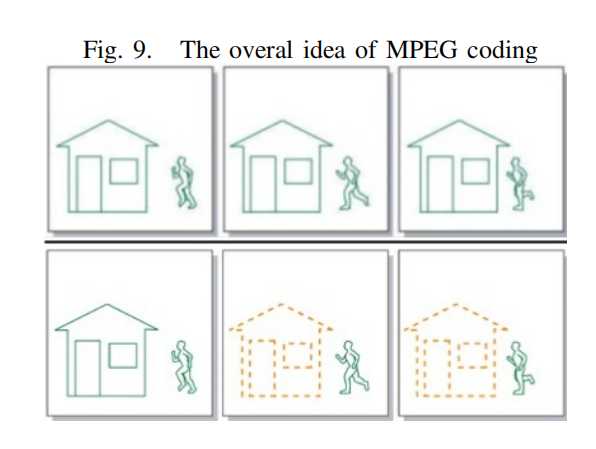
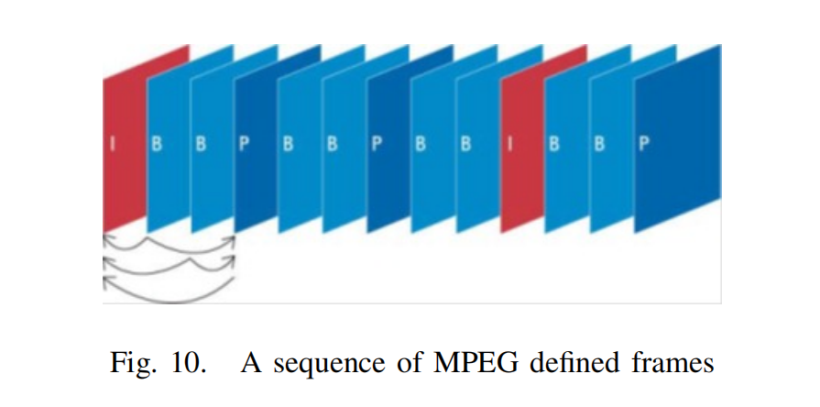
在MPEG編碼算法中,我們只對視頻序列中的新部分和視頻中運動部分的信息進行編碼。例如,考慮圖9,上面的三張圖。對于壓縮我們只需考慮新的部分,如圖9,我們只需要考慮底部的三個序列。視頻壓縮的基本原理是圖像對圖像的預測。一組圖像中的第一個圖像是i幀。這些幀顯示開始一個心得場景,因此不需要被壓縮,因為他們沒有依賴于該圖像之外。但其他幀可以使用第一張圖片的一部分作為參考。從一個參考圖像預測的圖像稱為p幀,從兩個其他參考圖像雙向預測的圖像稱為B幀。因此,總的來說,我們將有以下幀MPEG編碼:
-
I-frames:獨立的;不需要參考幀預測
-
P幀:從最后一個I或P參考幀預測
-
B-frames:雙向:從兩個參考幀預測,一個在過去,一個在未來,將考慮最佳匹配。
MPEG應用程序:MPEG在現實世界中有很多的應用。我們在此列舉其中一些:
1、有限電視。一些電視系統通過有線電視線路發送MPEG-II節目
2、直接廣播衛星。MPEG視頻流被跌形/解碼器接收,它提取的數據為標準NTSC電視信號。
3、媒體的金庫。Silicon Graphics、Storage Tech和其他供應商正在生產按需視頻系統,在一個安裝上有兩萬個文件MPEG編碼的電影。
4、實時編碼,這仍是專業人士的專屬領域。結合特殊用途的并行硬件,實時編碼器的成本可達2萬至5萬美元。
11.今天的數據壓縮:應用程序和問題
11.1網絡
今天隨著用戶數量的增加和遠程辦公,以及使用云計算的應用程序部署模型的出現,更多正在傳輸的數據對網絡連接的壓力導致了額外的問題。
數據壓縮重要的作用之一是將其應用于計算機網絡。然而,在帶寬有限的網絡環境下,實現高的壓縮比是提高應用程序性能的必要條件,如果壓縮比過低,網絡將保持飽和,性能增益將非常小。同樣,如果壓縮速度過低,壓縮機也會成為瓶頸。許多網絡數據的傳輸優化解決方案都只關注網絡層的優化。這些解決方案不僅缺乏靈活性,而且沒有包含能夠進一步增強通過網絡鏈接傳輸數據的應用程序性能的優化。
11.2基于報文或會話的壓縮
許多網絡壓縮系統是基于數據包的。基于數據包的壓縮系統使用解壓器緩沖發送到遠程網絡的數據包。然后,這些數據包在單個時間內或作為一個組被壓縮,然后發送到解壓器,在那里這個過程被逆轉。
當壓縮數據包時,這些系統必須在將小數據包寫入網絡和執行額外的工作來聚合和封裝多個數據包寫入網絡和執行額外的工作來聚合和封裝多個數據包之間做出選擇,這兩種選擇都不會產生最佳效果。向網絡寫入小數據包會增加TCP/IP報頭的開銷,而聚合和封裝數據包會增加流的封裝報頭。
11.3字典壓縮大小
幾乎所有壓縮實用程序的一個共同限制是有限的儲存空間。
與對網絡的請求相似,并不是所有在網絡上傳輸的字節都以相同的頻率重復。一些字節模式出現的頻率很高,因為他們是流行文檔或公共網絡協議的一部分。其他字節模式只出現一次,并且永遠不重復。經常重復的字節序列和不經常重復的字節序列之間的關系可以在Zipfs定律中看到。
11.4基于塊或基于字節的壓縮
基于塊的壓縮系統儲存先前在網絡上傳輸的數據片段。當第二次遇到這些塊時,對這些網塊的引用被傳輸到遠程設備,然后遠程設備重新構建原始數據。
基于塊的系統的一個關鍵缺點是,重復的數據幾乎從不與塊的長度完全相同。因此,匹配通常只是部分匹配,不壓縮一些重復的數據。如圖12說明了使用256字節塊的系統試圖壓縮512自治街的數據時會發生什么。

11.5能源效率
能源效率領域,尤其是無線傳感器網絡是當今世界最熱門的網絡研究領域之一。無線傳感器網絡由分布在空間上的傳感器組成,用于檢測物理或環境條件,如溫度、聲音、振動、壓力、運動或污染物,并協同將他們的數據通過網絡傳遞到主要位置。而傳感器的大小和成本限制導致了資源的限制,如能源、內存、計算速度和通信帶寬。巨大共享傳感器之間的數據需要能量高效、低延遲和高精度。
目前,如果傳感器系統設計者想要壓縮獲得的數據,他們必須卡法特定于應用程序的壓縮算法,或者使用非為資源所限的傳感器節點設計的現成算法。
主要的嘗試是實現一種專門為傳感器網絡設計的傳感器Lempel-Ziv(S-LZW)壓縮算法。針對無線傳感網絡中設計高效數據壓縮算法的趨勢,Vidhyapriyal和P.Vanathi設計并實現了兩種集成了最短路徑路由技術的無損數據壓縮算法,以減少原始數據的大小,并在傳感器網絡中實現速率、能量和精度之間的最佳權衡。
12.總結
在數據存儲和信息傳輸量不斷增長的今天,數據壓縮技術發揮著重要作用。即使在帶寬和存儲能力方面有了進步,如果數據沒有被壓縮,許多應用程序的成本將太高,用戶無法使用他們。本文我們嘗試介紹了無損壓縮和有損壓縮兩種壓縮類型,以及數據壓縮中的一些主要概念、算法和方法,并討論了他們的不同應用和工作方式,然后我們探討了兩個主要的日常應用;以JPEG為例進行圖像壓縮,以MPEG為例進行了視頻壓縮。最后我們討論了當今數據壓縮的主要應用和存在的問題。
< 本文完>
ELT.ZIP是誰?
ELT<=>Elite(精英),.ZIP為壓縮格式,ELT.ZIP即壓縮精英。
成員:
上海工程技術大學大二在校生閆旭
合肥師范學院大二在校生楚一凡
清華大學大二在校生趙宏博
成都信息工程大學大一在校生高云帆
黑龍江大學大一在校生高鴻萱
山東大學大三在校生張智騰

ELT.ZIP是來自6個地方的同學,在OpenHarmony成長計劃啃論文俱樂部里,與來自華為、軟通動力、潤和軟件、拓維信息、深開鴻等公司的高手一起,學習、研究、切磋操作系統技術...
寫在最后
OpenHarmony 成長計劃—“啃論文俱樂部”(以下簡稱“啃論文俱樂部”)是在 2022年 1 月 11 日的一次日常活動中誕生的。截至 3 月 31 日,啃論文俱樂部已有 87 名師生和企業導師參與,目前共有十二個技術方向并行探索,每個方向都有專業的技術老師帶領同學們通過啃綜述論文制定技術地圖,按“降龍十八掌”的學習方法編排技術開發內容,并通過專業推廣培養高校開發者成為軟件技術學術級人才。
啃論文俱樂部的宗旨是希望同學們在開源活動中得到軟件技術能力提升、得到技術寫作能力提升、得到講解技術能力提升。大學一年級新生〇門檻參與,已有俱樂部來自多所高校的大一同學寫出高居榜首的技術文章。
如今,搜索“啃論文”,人們不禁想到、而且看到的都是我們——OpenHarmony 成長計劃—“啃論文俱樂部”的產出。
OpenHarmony開源與開發者成長計劃—“啃論文俱樂部”學習資料合集
1)入門資料:啃論文可以有怎樣的體驗
https://docs.qq.com/slide/DY0RXWElBTVlHaXhi?u=4e311e072cbf4f93968e09c44294987d
2)操作辦法:怎么從啃論文到開源提交以及深度技術文章輸出https://docs.qq.com/slide/DY05kbGtsYVFmcUhU
3)企業/學校/老師/學生為什么要參與 & 啃論文俱樂部的運營辦法https://docs.qq.com/slide/DY2JkS2ZEb2FWckhq
4)往期啃論文俱樂部同學分享會精彩回顧:
同學分享會No1.成長計劃啃論文分享會紀要(2022/02/18)https://docs.qq.com/doc/DY2RZZmVNU2hTQlFY
同學分享會No.2 成長計劃啃論文分享會紀要(2022/03/11)https://docs.qq.com/doc/DUkJ5c2NRd2FRZkhF
同學們分享會No.3 成長計劃啃論文分享會紀要(2022/03/25)
https://docs.qq.com/doc/DUm5pUEF3ck1VcG92?u=4e311e072cbf4f93968e09c44294987d
現在,你是不是也熱血沸騰,摩拳擦掌地準備加入這個俱樂部呢?當然歡迎啦!啃論文俱樂部向任何對開源技術感興趣的大學生開發者敞開大門。

掃碼添加 OpenHarmony 高校小助手,加入“啃論文俱樂部”微信群
后續,我們會在服務中心公眾號陸續分享一些 OpenHarmony 開源與開發者成長計劃—“啃論文俱樂部”學習心得體會和總結資料。記得呼朋引伴來看哦。
原文標題:統計壓縮編碼機理分析(下篇)
文章出處:【微信公眾號:開源技術服務中心】歡迎添加關注!文章轉載請注明出處。
-
開源技術
+關注
關注
0文章
389瀏覽量
7963 -
OpenHarmony
+關注
關注
25文章
3728瀏覽量
16395
原文標題:統計壓縮編碼機理分析(下篇)
文章出處:【微信號:開源技術服務中心,微信公眾號:共熵服務中心】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Minitab 在統計分析中的應用
Lua語法基礎教程(下篇)
Huffman壓縮算法概述和詳細流程
音頻信號的無損壓縮編碼是什么
示波器統計曲線和故障分析pass/fail測試
眾鑫創展----1080P十倍光學變焦攝像頭方案

鴻蒙OpenHarmony南向:【Hi3516開發板介紹】
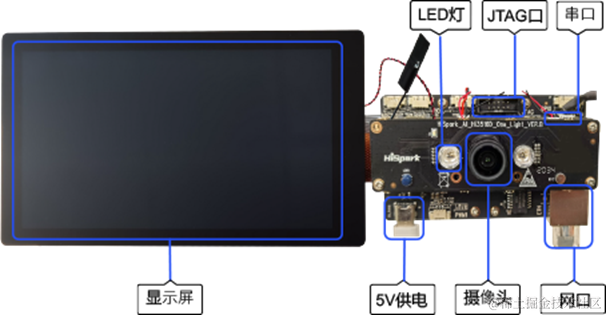
【RTC程序設計:實時音視頻權威指南】音視頻的編解碼壓縮技術
FFmpeg創始人為音頻壓縮工具TSAC,將音頻壓縮至極低比特率
谷歌推出Jpegli開源編碼庫,優化圖片壓縮,提升圖像品質
在CPU芯片領域,中國將迎來新型服務器的發展機遇,




 統計壓縮編碼機理分析(下篇)
統計壓縮編碼機理分析(下篇)













評論