一、前言
粒子濾波(particle filter)是一種常見的濾波算法,廣泛應用于目標跟蹤、移動機器人等領域。網絡上有不少關于粒子濾波的資料,但大多是直接給出了粒子濾波的相關公式和證明,或較為直觀上的解釋。作者在學習粒子濾波的過程中對一些概念和操作時常感到突兀,后來發(fā)現想要完整了解粒子濾波,需要首先了解前因,逐漸深入才能理解粒子濾波,而不是直接學習粒子濾波這個方法。
本文將側重從“粒子濾波是怎么來的”這個問題介紹粒子濾波。限于篇幅與易懂性,對一些概念并沒有展開介紹,讀者在了解基本思路后可以根據給出的資料深入學習。本文包含了作者自己不嚴謹的理解與闡述,如有疏漏,望批評指正。
二、對“濾波”的一些介紹
2.1 何為“濾波”?
貝葉斯濾波、卡爾曼濾波、粒子濾波……種種這些濾波方法,都涉及到了“濾波”這個詞。那么到底什么是濾波,不同的領域有不同的定義。比如在信號系統(tǒng)領域,濾波是指將信號中特定波段的頻率濾除的操作。而在移動機器人領域,我暫時沒有看到較為嚴格的定義。我認為可以姑且理解為:通過不斷地觀測,使得對目標狀態(tài)的估計變得更加準確。
2.2 貝葉斯濾波
卡爾曼濾波與粒子濾波都是基于貝葉斯濾波框架下的濾波算法。講粒子濾波便不得不提貝葉斯濾波。貝葉斯濾波的基本思想是根據上一時刻的狀態(tài)對當前狀態(tài)進行預測,并根據此時的觀測進行更新。基本算法是:
(圖片來源:《概率機器人》) 可以看出,在預測部分需要求一個積分,而這個積分往往很難求。所以顯有方法可以直接利用原始的貝葉斯進行處理。
2.3 卡爾曼濾波
卡爾曼濾波也是非常龐大的一塊內容,這里不展開介紹。只在這里說明,卡爾曼濾波是貝葉斯濾波在線性高斯系統(tǒng)下的一種濾波算法。而對于非線性系統(tǒng),則衍生出來了擴展卡爾曼濾波。同時指出,無論是卡爾曼還是擴展卡爾曼濾波,都是參數化的濾波方法,對于無法用參數化進行表示的,則采用粒子濾波。粒子濾波是一種無參的濾波算法。
三、積分計算:從蒙特卡洛說起
3.1 分段近似法求積分
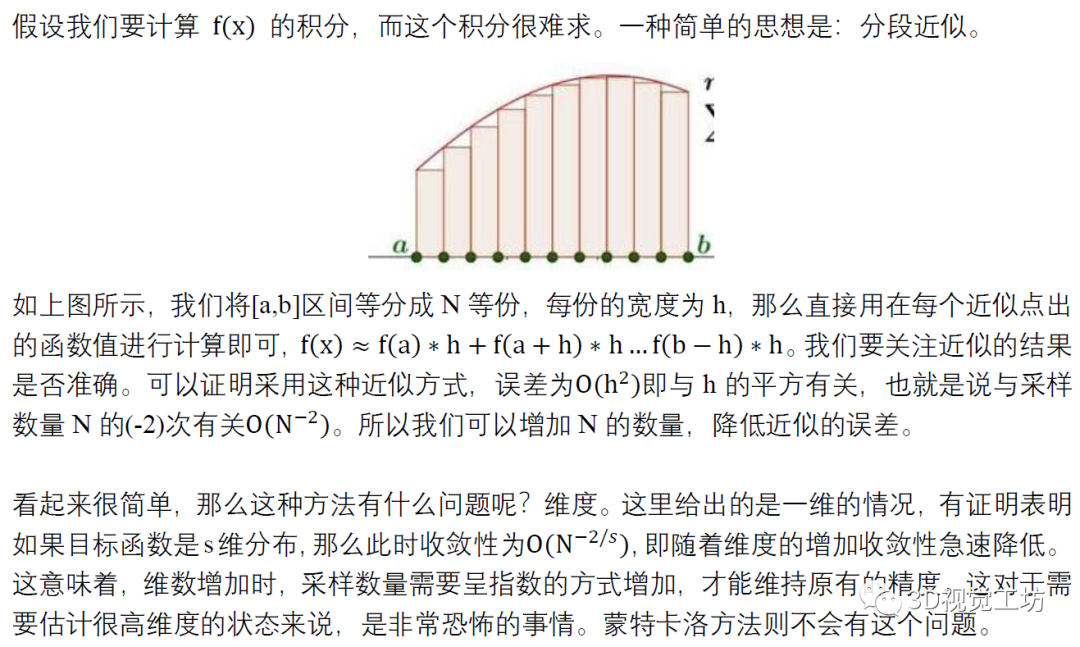
3.2 蒙特卡洛采樣求積分
(此處略過蒙特卡洛基本原理)
3.2.1 簡單的均勻采樣
求積分和求期望是相同的。假設我們對一個分布求取積分,采用最簡單的采樣方式——均勻采樣。我們求取在x滿足均勻分布u(x)時,f(x)在[a,b]的期望I。按照分布u(x)進行N次隨機采樣:
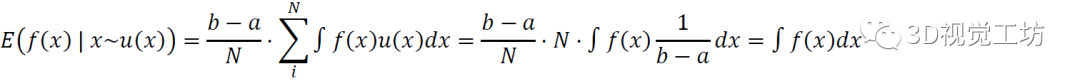
可以發(fā)現最后一項對f(x)的積分,就是x的期望。所以我們可以發(fā)現,當我們按照均勻分布u(x)對x進行大量采樣,計算對應的f(x)的平均值,就是f(x)的積分。
3.2.2 任意分布的采樣
下面我們研究,如果不是按照均勻分布u(x)采樣,而是任意分布p(x)進行采樣,結果如何。此時
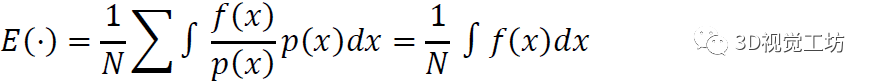
依舊與原始的積分相同。所以我們得出了重要的結論:在蒙特卡洛時,我們可以按照任意分布進行采樣,再計算對應f(x)的積分。

這一點很好理解,如果我們選擇的分布p(x)就是真實的分布,那么我們從p(x)進行采樣,就和直接從真實分布進行采樣是一樣的,積分結果當然是沒有誤差的。這提醒我們,在選取p(x)分布時要盡可能的與實際分布接近,從而極大程度的降低方差,從而減少需要采樣的數量。
四、重要性采樣與序列重要性采樣
4.1 重要性采樣(Importance Sampling, IS)

4.2 序列重要性采樣(Sequential Importance Sampling, SIS)


4.3 重采樣(Resampling)
在實際過程中,我們發(fā)現利用權重更新公式進行更新時,在幾次迭代之后,權重的分布會極其不均勻,出現個別粒子權重很大接近于1,而其他的都接近于0的情況。這時候采用了一種“重采樣”策略,即每次權重更新之后,根據當前權重對所有粒子進行重采樣,之后將所有權重設定為相同。這樣我們用粒子的數量代替了粒子的權重,避免了權重的不均勻。
5. 粒子濾波(Particle Filter)

此時對權重更新公式進行變形(在不產生歧義情況下部分內容用點省略):


6. 總結
本文首先從濾波問題說起,指出了貝葉斯濾波框架下積分很難求的問題。由此引出蒙特卡洛方法。之后為了降低誤差、減少運算量和避免權重集中,對應出現了重要性采樣、序列重要性采樣與重采樣,順理成章的得出了粒子濾波的數學原理,之后給出了對應的物理模型。最后給出了簡單的粒子濾波的完整算法。
審核編輯:劉清
-
濾波算法
+關注
關注
2文章
88瀏覽量
13718 -
貝葉斯算法
+關注
關注
1文章
7瀏覽量
9067
原文標題:粒子濾波到底是怎么得到的?
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦
高斯濾波和均值濾波的區(qū)別
高斯濾波和雙邊濾波的區(qū)別
emi濾波器是什么濾波器
陷波濾波器怎么進行濾波
貝葉斯濾波和卡爾曼濾波的區(qū)別
濾波器濾波的本質:信號時頻特性的選擇與處理|維愛普電源濾波器

高通濾波器、低通濾波器、帶通濾波器怎樣測幅頻特性?
電容濾波電路中選擇濾波電容的原則是
濾波電容可以加大容量嗎 濾波電容并聯小電容對聲音的影響
濾波電路有哪些類型 如何判斷濾波電路的類型
有源低通濾波器設計原理 有源低通濾波器的截止頻率計算
如何使用濾波器來進行有效的信號濾波?
如何使用EMI濾波器來抑制噪聲




 何為濾波?粒子濾波是怎么來的?
何為濾波?粒子濾波是怎么來的?











評論