運(yùn)動(dòng)介質(zhì)的電動(dòng)力學(xué)，這個(gè)啟發(fā)愛(ài)因斯坦那一代科學(xué)家發(fā)展出狹義相對(duì)論的著名問(wèn)題，最近再一次成為中國(guó)科技界的熱點(diǎn)話題。在熱烈的討論過(guò)程中，有一個(gè)問(wèn)題反復(fù)出現(xiàn)，就是對(duì)于描寫電磁場(chǎng)運(yùn)動(dòng)規(guī)律的麥克斯韋方程組，有非相對(duì)論極限嗎？當(dāng)運(yùn)動(dòng)介質(zhì)的速度遠(yuǎn)低于光速的時(shí)候，我們可以不考慮相對(duì)論效應(yīng)，用伽利略變換來(lái)近似洛倫茲變換嗎？經(jīng)過(guò)討論，筆者發(fā)現(xiàn)許多科技工作者對(duì)這個(gè)問(wèn)題存在不同程度的誤解，其中最大的一個(gè)就是以為介質(zhì)速度不快就沒(méi)有相對(duì)論效應(yīng)，伽利略變換也近似可用。造成這一誤解的主要原因還是對(duì)狹義相對(duì)論的理解不夠透徹，尤其是對(duì)狹義相對(duì)論與經(jīng)典電磁學(xué)之間的密切聯(lián)系缺乏認(rèn)識(shí)。下面，筆者將通過(guò)這篇短文，專門介紹一下洛倫茲變換的低速近似問(wèn)題。

01只有在研究告訴運(yùn)動(dòng)的物體時(shí)才需要 狹義相對(duì)論嗎？

許多介紹相對(duì)論的科普文章和教科書都以相對(duì)論力學(xué)為主要介紹對(duì)象，這一方面是因?yàn)榱W(xué)研究的對(duì)象更貼近人們的生活，另一方面也是為了方便“炫耀”相對(duì)論的神奇，以便把“時(shí)間旅行”、“回到未來(lái)”這些荒誕不經(jīng)的幻想和薛定諤的那只貓一樣，推上大眾文化的餐桌，反復(fù)消費(fèi)。其實(shí)，狹義相對(duì)論是19世紀(jì)下半葉科學(xué)家們?cè)谘芯侩姶努F(xiàn)象的時(shí)候逐步建立起來(lái)的。在筆者看來(lái)，對(duì)電磁現(xiàn)象而言，狹義相對(duì)論的出現(xiàn)非常自然和必要，相反非相對(duì)論的電磁世界才是荒唐且不合邏輯的。實(shí)際上，狹義相對(duì)論的提出，正是為了統(tǒng)一力學(xué)世界和電磁世界中關(guān)于參照系變換截然不同的觀念[1]。讓我們先從相對(duì)性原理講起。

相對(duì)性原理是一條自然界的公理，即物理規(guī)律在任何慣性參照系下都保持一致。我們很容易檢驗(yàn)，經(jīng)典的牛頓力學(xué)滿足相對(duì)性原理。在通過(guò)伽利略變換，把時(shí)空坐標(biāo)從一個(gè)參照系變換到另一個(gè)參照系后，物體的坐標(biāo)、速度、動(dòng)量等都會(huì)發(fā)生改變；但決定這些物理量演化的規(guī)律保持相同的形式，即牛頓三大定律在不同的慣性系下保持完全一樣的形式。比如牛頓第一定律：當(dāng)一個(gè)物體處于不受力的狀態(tài)時(shí)，它的速度保持不變。在實(shí)驗(yàn)室參照系S下牛頓第一定律可以寫成u=常數(shù)。現(xiàn)在假設(shè)一個(gè)以速度v相對(duì)于實(shí)驗(yàn)室參照系勻速直線運(yùn)動(dòng)的S′系，根據(jù)牛頓力學(xué)背后的絕對(duì)時(shí)空觀，我們可以用如下伽利略變換建立不同慣性系下的坐標(biāo)(x，y，z，t)和(x′，y′，z′，t′)之間的關(guān)系：x′=x-vt；y′=y；z′=z；t′=t，并得到在S′系下牛頓第一定律的形式為u′=u-v=常數(shù)。可以看到，雖然在不同慣性系下觀察者分別測(cè)到不同的速度u和u′，但不受外力的物體的運(yùn)動(dòng)速度在各自的參考系下均保持不變，這一運(yùn)動(dòng)學(xué)規(guī)律的形式是完全一致的。

從上面的例子可以看到，相對(duì)性原理在牛頓力學(xué)中是非常顯然的。但是在電磁世界里則完全相反：如果還是堅(jiān)持牛頓力學(xué)的絕對(duì)時(shí)空觀，用伽利略變換來(lái)聯(lián)系不同慣性系的話，相對(duì)性原理是顯然不成立的。或者也可以這樣說(shuō)，要使電磁現(xiàn)象的規(guī)律滿足相對(duì)性原理，我們需要時(shí)空坐標(biāo)以不同于伽利略變換的方式變換。下面就來(lái)看一個(gè)非常簡(jiǎn)單的例子[2]，假設(shè)在實(shí)驗(yàn)室系S中有一個(gè)試探點(diǎn)電荷被置于在一根沿著z方向的通電導(dǎo)線的附近x處，試探電荷保持靜止，導(dǎo)線保持電中性并通以電流I=env，其中n是導(dǎo)線中電子的線密度，v是電子的漂移速度。在S系的觀測(cè)者看來(lái)，導(dǎo)線中的電子以-v的速度沿著反方向運(yùn)動(dòng)而正電荷保持靜止，從而形成+z方向的電流I，又由于電子和正電荷的線密度相等，都為n，因此正負(fù)電荷完全抵消，導(dǎo)線是電中性的。根據(jù)電磁學(xué)知識(shí)，我們可以輕松得到試探電荷處的磁場(chǎng)強(qiáng)度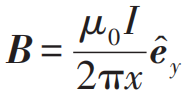。由于我們考慮的試探電荷在實(shí)驗(yàn)室系中處于靜止?fàn)顟B(tài)，因而受到的洛倫茲力嚴(yán)格為零；再加上導(dǎo)線是電中性的，在試探電荷處不產(chǎn)生任何電場(chǎng)，在實(shí)驗(yàn)室系的觀測(cè)者看來(lái)，試探電荷受到的總的電磁力嚴(yán)格為零，電荷不會(huì)產(chǎn)生任何運(yùn)動(dòng)。總結(jié)一下，在S系的觀測(cè)者看來(lái)，??

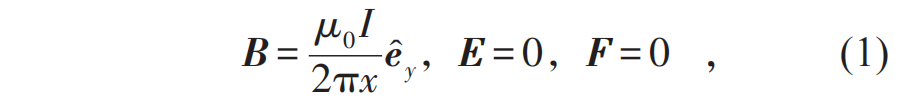
下面讓我們換到另一個(gè)慣性參照系S′來(lái)觀測(cè)同一個(gè)物理過(guò)程。現(xiàn)在我們選擇的參照系是以導(dǎo)線中電子的漂移速度-v沿著導(dǎo)線勻速運(yùn)動(dòng)的參照系。如果按照牛頓力學(xué)的觀點(diǎn)對(duì)時(shí)空坐標(biāo)做如下伽利略變換：

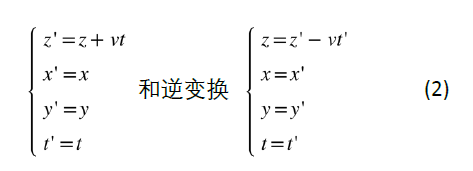
那么在S′參照系的觀察者看來(lái)，試探電荷以v的速度運(yùn)動(dòng)，導(dǎo)線中的電子是靜止的，而正電荷以v的速度沿著導(dǎo)線運(yùn)動(dòng)。根據(jù)電流的定義，我們得到在S′系的電流I′不變，還是等于S系中觀測(cè)到的電流I，同時(shí)導(dǎo)線依然是電中性的，從而產(chǎn)生與S系中一樣的電磁場(chǎng)。現(xiàn)在我們可以總結(jié)一下對(duì)這一問(wèn)題進(jìn)行伽利略變換得到的結(jié)果：在S′系中觀測(cè)到的電磁場(chǎng)嚴(yán)格等于在S系中的電磁場(chǎng)，也就是在伽利略變換下電磁場(chǎng)不變E′ =E,B′ =B，因?yàn)楫a(chǎn)生它們的“源”：電流和電荷密度都不變。但是，原先在S系中靜止的試探電荷，在S′系的觀測(cè)者看來(lái)以v的速度沿著導(dǎo)線方向運(yùn)動(dòng)，從而受到一個(gè)指向?qū)Ь€的大小

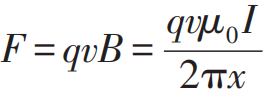
的洛倫茲力，并向著導(dǎo)線方向加速運(yùn)動(dòng)。

現(xiàn)在問(wèn)題來(lái)了，同一個(gè)物理過(guò)程，實(shí)驗(yàn)室參照系S和運(yùn)動(dòng)參照系S′的兩個(gè)觀察者得出截然不同的結(jié)論！一個(gè)認(rèn)為試探電荷不受力，與導(dǎo)線之間的距離保持不變；另一個(gè)卻認(rèn)為試探電荷會(huì)受力并加速運(yùn)動(dòng)。這個(gè)簡(jiǎn)單的案例，給出了對(duì)一個(gè)經(jīng)典電磁學(xué)問(wèn)題用伽利略變換進(jìn)行時(shí)空坐標(biāo)變換的一個(gè)佯謬。那么到底誰(shuí)對(duì)誰(shuí)錯(cuò)，又是在哪個(gè)環(huán)節(jié)出了問(wèn)題？是相對(duì)性原理不適用于電磁現(xiàn)象？還是伽利略變換不適用于電磁現(xiàn)象？

這是19世紀(jì)末物理學(xué)界最令人抓狂的問(wèn)題，最后由那一代物理學(xué)家中的杰出代表洛倫茲、龐加萊和愛(ài)因斯坦等給出了令人信服的答案——狹義相對(duì)論。針對(duì)上述佯謬，答案應(yīng)該是S系中觀察者的觀點(diǎn)是對(duì)的，電荷不受力。那么S′系的觀察者做錯(cuò)了哪一點(diǎn)呢？問(wèn)題出在從S系到S′系的時(shí)空坐標(biāo)變換。狹義相對(duì)論告訴我們，在兩個(gè)慣性參照系之間，嚴(yán)格的時(shí)空坐標(biāo)變換形式是洛倫茲變換而不是伽利略變換，無(wú)論對(duì)力學(xué)現(xiàn)象還是電磁現(xiàn)象都是如此。只是對(duì)于牛頓力學(xué)研究的宏觀物體來(lái)說(shuō)，伽利略變換是在低速(遠(yuǎn)低于光速)下的很好近似。然而對(duì)于電磁場(chǎng)這樣的規(guī)范場(chǎng)來(lái)講，它對(duì)應(yīng)的微觀粒子——光子是無(wú)質(zhì)量的，如果要保留電磁場(chǎng)方程自身的動(dòng)力學(xué)，在任何情況下伽利略變換都不是一個(gè)物理上可接受的近似。比如上述佯謬就是一個(gè)典型案例，哪怕運(yùn)動(dòng)速度v遠(yuǎn)遠(yuǎn)低于光速，這個(gè)問(wèn)題還是一樣存在，是定性而非定量的錯(cuò)誤問(wèn)題。實(shí)際上對(duì)S′參照系中的觀測(cè)者來(lái)說(shuō)，他觀測(cè)到的電流I′并不等于I，更重要的是他測(cè)到的導(dǎo)線不再是電中性的而是帶有均勻的電荷密度ρ′！正是電荷密度ρ′產(chǎn)生的徑向電場(chǎng)嚴(yán)格抵消掉了磁場(chǎng)產(chǎn)生的洛倫茲力，使得S′參照系中的觀測(cè)者得到跟S系中一樣的總力嚴(yán)格為零的結(jié)論，從而滿足相對(duì)性原理。

接下來(lái)我們仔細(xì)介紹一下如何用洛倫茲變換來(lái)解決上述佯謬。首先利用洛倫茲變換寫出分別在實(shí)驗(yàn)室參考系S和運(yùn)動(dòng)參考系S′中測(cè)到的時(shí)空坐標(biāo)(x，y，z，t)和(x′，y′，z′，t′)之間的變換關(guān)系：

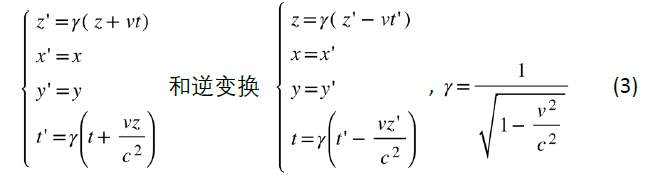
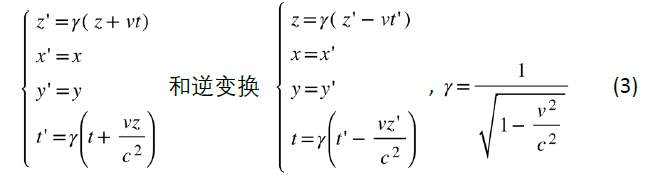
用一個(gè)簡(jiǎn)單的物理假設(shè)來(lái)理解導(dǎo)線中的電流I，就是在實(shí)驗(yàn)室系S中，導(dǎo)線中的電子一個(gè)個(gè)間隔均勻排列并以勻速-v沿著z方向運(yùn)動(dòng)，而正電荷也以同樣的均勻的間隔排列并保持靜止。在這一假想實(shí)驗(yàn)中，我們?cè)O(shè)定S系中的觀測(cè)者測(cè)得導(dǎo)線是電中性的，即在S系中負(fù)電荷之間的間隔d-嚴(yán)格等于正電荷之間的間隔d+，設(shè)d-=d+=d，對(duì)應(yīng)的正負(fù)電荷線密度的絕對(duì)值為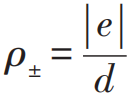，電流為。

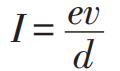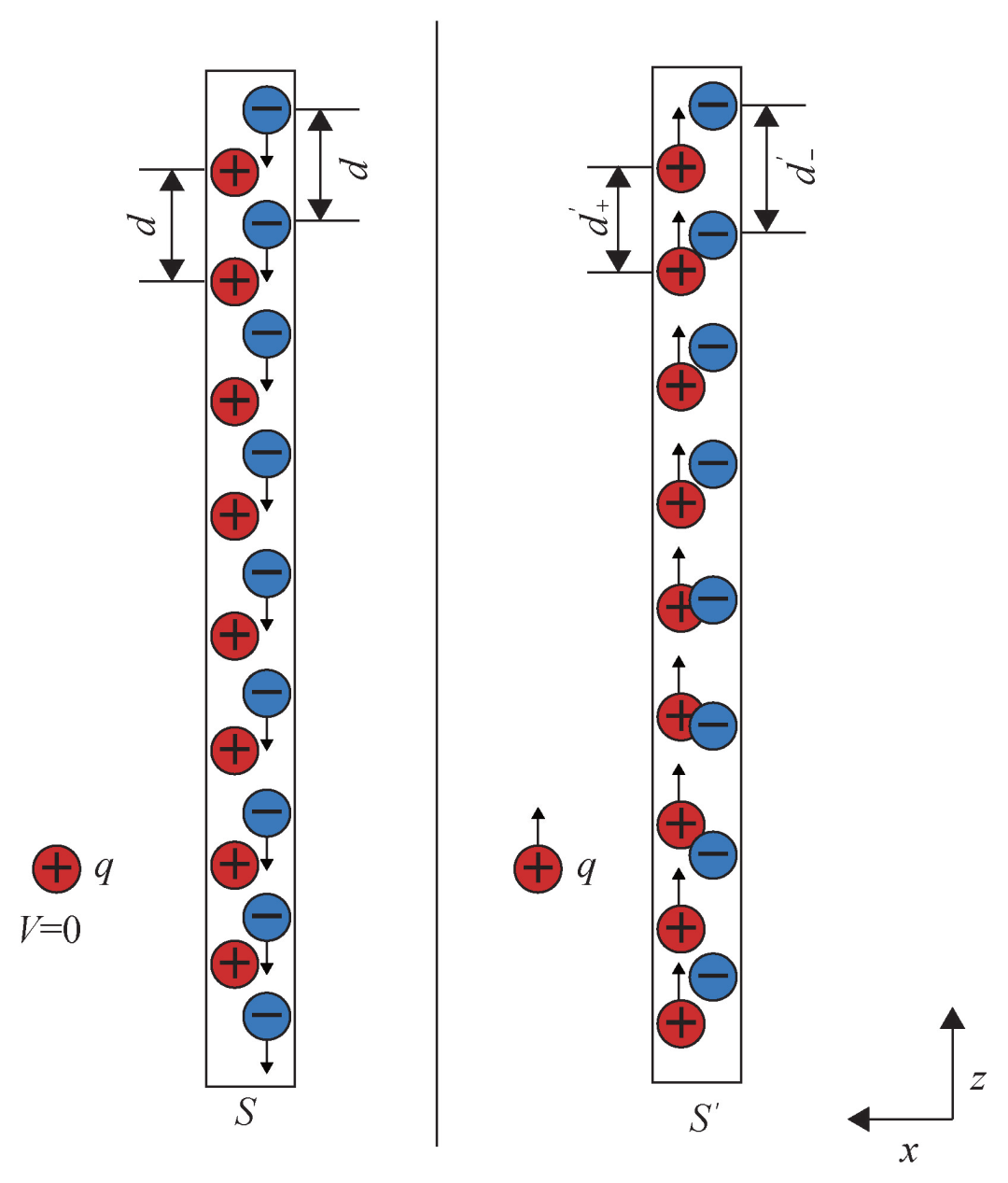
圖1 在洛倫茲變換下，兩個(gè)慣性參照系S和S′中電荷運(yùn)動(dòng)情況

現(xiàn)在換到跟負(fù)電荷一起以-v速度沿著z方向運(yùn)動(dòng)的S′系。在S′系的觀測(cè)者看來(lái)負(fù)電荷是靜止的，而正電荷以速度v沿著z方向運(yùn)動(dòng)。跟伽利略變換不一樣的是，在洛倫茲變換下，電荷之間的間距要發(fā)生變化，如圖1所示，導(dǎo)致在S′系里正負(fù)電荷的密度是不一樣的，從而在導(dǎo)線中產(chǎn)生凈電荷密度。那么如何得到S和S′系中不同的電荷間距關(guān)系呢？這就要用到上面給出的洛倫茲變換。先來(lái)看S系的觀測(cè)者是如何理解以-v速度勻速運(yùn)動(dòng)的負(fù)電荷間距的，在他看來(lái)，相鄰兩個(gè)負(fù)電荷之間的空間距離是由下面兩個(gè)時(shí)空事件之間“時(shí)空距離”的空間分量來(lái)確定的。時(shí)空事件一：第N號(hào)負(fù)電荷在時(shí)刻t位于時(shí)空坐標(biāo)(x，y，z1，t)處；時(shí)空事件二：相鄰的第N-1號(hào)負(fù)電荷在同時(shí)刻t位于空間坐標(biāo)(x，y，z2，t)處，于是在S系中測(cè)到負(fù)電荷之間的間距d-=z2-z1。這兩次測(cè)量事件在運(yùn)動(dòng)的S′系中對(duì)應(yīng)的時(shí)空坐標(biāo)分別為(x′，y′，z′1，t′1)和(x′，y′，z′2，t′2)。這里要注意，狹義相對(duì)論的一個(gè)重要結(jié)論是所謂“同時(shí)性”是相對(duì)的，在S系中看起來(lái)是同時(shí)的兩個(gè)測(cè)量事件在S′系中并不同時(shí)，因此t′1并不等于t′2，但在S′系中負(fù)電荷是靜止的。因此，跟S系的觀測(cè)者不同，為了確定相鄰負(fù)電荷之間的間距，S′系的觀測(cè)者并不需要兩次測(cè)量是同時(shí)的；換句話說(shuō)，他同樣可以利用這兩次時(shí)空事件的坐標(biāo)得到S′參照系中的負(fù)電荷間距d'-=z'2-z'1。現(xiàn)在我們就可以通過(guò)上面列出的洛倫茲變換公式得到d′-=γd-，由于γ是一個(gè)總是大于1的因子，因此一個(gè)勻速運(yùn)動(dòng)的物體在其運(yùn)動(dòng)方向上的長(zhǎng)度要縮短一個(gè)因子γ-1，這就是狹義相對(duì)論里非常著名的“尺縮”效應(yīng) (與距離的尺縮效應(yīng)相對(duì)應(yīng)，時(shí)間差在變換參考系后延長(zhǎng)一個(gè)因子γ稱為“鐘慢”效應(yīng)[3]) 。同樣的分析也適用于正電荷的情況，唯一不同的是，對(duì)正電荷來(lái)說(shuō)情況正好相反，在S系中靜止，而在S′系中勻速運(yùn)動(dòng)，因此可以得到d′+=γ-1d+。比較一下上面得到的S′系中正負(fù)電荷間距d′+和d′-，可以明顯看出它們并不相等，因此S′系中的導(dǎo)線是帶電的，凈電荷線密度為

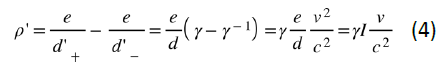
而電流為

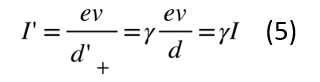
現(xiàn)在我們已經(jīng)得到S′系中的電荷密度ρ′和電流強(qiáng)度I′，下一步可以計(jì)算由上述電荷密度和電流強(qiáng)度引起的電磁場(chǎng)和試探電荷q的受力情況了。再提醒一下，在S′系里的試探電荷q以v沿著z方向運(yùn)動(dòng)。簡(jiǎn)單的計(jì)算過(guò)程如下：

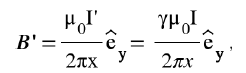
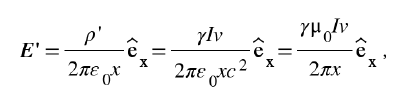
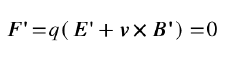
結(jié)果是，在S′系的觀測(cè)者同樣得出試探電荷受力為零的結(jié)果，相對(duì)性原理得到滿足。注意，在上面的推導(dǎo)中我們用到了光速c的定義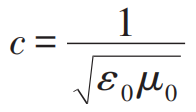。從上面的結(jié)果可以看出，不管速度v的數(shù)值有多小，只有正確地運(yùn)用洛倫茲變換，不同參照系的觀測(cè)者們才能達(dá)成一致。在一個(gè)參照系里的觀測(cè)者只看到磁場(chǎng)，而在另一個(gè)系里的觀測(cè)者則同時(shí)測(cè)到磁場(chǎng)和電場(chǎng)，不同參照系下的場(chǎng)量不一樣，但滿足各自參照系下完全一樣的麥克斯韋方程組，這就叫相對(duì)論協(xié)變性。那么洛倫茲變換能不能做低速近似呢？當(dāng)然是可以的，洛倫茲變換形式中含有v/c因子，可以做小量展開(kāi)，最低階是一階，也就是把上式中所有的γ因子都近似成1。但從上面這個(gè)簡(jiǎn)單的例子可以看出，即使對(duì)v/c展開(kāi)到一階，電磁場(chǎng)E和B也要發(fā)生變化，對(duì)電磁場(chǎng)來(lái)說(shuō)，洛倫茲變換的低速極限永遠(yuǎn)不是伽利略變換。同時(shí)，也要提醒大家，如果把洛倫茲變換展開(kāi)到v/c的一階，那么相對(duì)論協(xié)變性也只滿足到v/c的一階。下面，我們就以推導(dǎo)動(dòng)體介質(zhì)的電動(dòng)力學(xué)方程為例，來(lái)介紹一下如何利用洛倫茲變換的低速展開(kāi)來(lái)研究具體的電磁學(xué)問(wèn)題。需要指出的是，在20世紀(jì)初，這一問(wèn)題是啟發(fā)愛(ài)因斯坦思考相對(duì)論的重要問(wèn)題，并最后由閔可夫斯基完美收官。但對(duì)于21世紀(jì)的我們來(lái)說(shuō)，這就是一道典型的電動(dòng)力學(xué)習(xí)題。這就像第一個(gè)造出輪子的人一定是天才，而第二個(gè)嘛可以算是個(gè)好學(xué)生，前提是他也能造得足夠圓。

02動(dòng)體介質(zhì)電動(dòng)力學(xué)方程

在介紹動(dòng)體介質(zhì)電動(dòng)力學(xué)之前，先來(lái)簡(jiǎn)單介紹一下何謂“介質(zhì)”。介質(zhì)指的是能對(duì)電磁場(chǎng)進(jìn)行響應(yīng)的各類物質(zhì)。最簡(jiǎn)單的介質(zhì)以產(chǎn)生電/磁偶極矩的方式對(duì)電磁場(chǎng)進(jìn)行響應(yīng)，其中電偶極子就是電荷分布缺乏中心對(duì)稱的分子，而磁偶極子在微觀上就是外層電子總角動(dòng)量不為零的分子，可以看作是存在著圍繞分子中心的微觀電流。在描寫宏觀連續(xù)介質(zhì)的電磁性質(zhì)時(shí)，我們引入兩個(gè)矢量P(r,t)和M(r,t)，分別代表空間r處的電/磁偶極矩密度。很容易證明，P(r,t)的散度?·P(r,t)=ρP(r,t)是介質(zhì)中的極化電荷密度，M(r,t)的旋度?×M(r,t)=Jm(r,t)則是相應(yīng)的分子電流密度。有了P(r,t)和M(r,t)，我們就可以討論介質(zhì)中的麥克斯韋方程組了。在此之前先澄清一點(diǎn)，在一些教材和文章里把以下這個(gè)麥克斯韋方程組說(shuō)成是所謂“真空里的”麥克斯韋方程組是很不嚴(yán)謹(jǐn)?shù)模驗(yàn)樗仁钦婵绽锏囊彩墙橘|(zhì)里的麥克斯韋方程組，只要方程右邊的電荷密度同時(shí)包含自由電荷和極化電荷，電流密度同時(shí)包含自由電流和分子電流密度即可，所以應(yīng)該稱之為普適或者基本麥克斯韋方程組。

曾在香港科技大學(xué)教了10年電動(dòng)力學(xué)的杜勝望老師曾對(duì)我提起，這一點(diǎn)他每次上課都是反復(fù)提醒，所以我們系畢業(yè)的學(xué)生大概是不會(huì)弄錯(cuò)了。為什么要那么較真，反復(fù)強(qiáng)調(diào)這個(gè)概念呢？這是因?yàn)橐獜?qiáng)調(diào)介質(zhì)里的電磁場(chǎng)是獨(dú)立的，并按照統(tǒng)一(跟真空中完全一樣的)動(dòng)力學(xué)規(guī)律演化的實(shí)實(shí)在在的物質(zhì)，不是依附于介質(zhì)的附庸，所以當(dāng)介質(zhì)開(kāi)始運(yùn)動(dòng)的時(shí)候，其中的電磁場(chǎng)不會(huì)“月亮走我也走”，寸步不離地跟著介質(zhì)一起運(yùn)動(dòng)。這一點(diǎn)跟介質(zhì)中的聲波存在本質(zhì)的不同。

在介質(zhì)中，電磁場(chǎng)會(huì)進(jìn)一步引起電磁響應(yīng)，即P和M，傳統(tǒng)電磁學(xué)里將P和M所對(duì)應(yīng)的極化電荷密度和分子電流密度與自由電荷產(chǎn)生的電荷/電流密度分開(kāi)處理，因此定義了兩個(gè)新的場(chǎng)量D和H，

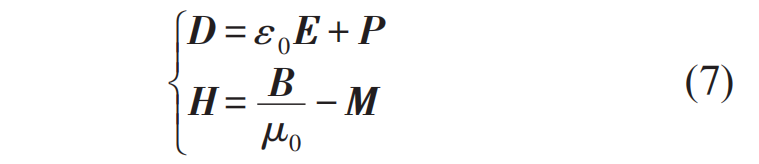
原則上這兩個(gè)介質(zhì)中的輔助場(chǎng)量(auxiliary fields)由介質(zhì)中的電磁場(chǎng)E和B自洽確定，而P，M和E，B(或者H)之間的關(guān)系稱為本構(gòu)關(guān)系，對(duì)于大部分介質(zhì)來(lái)說(shuō)，這個(gè)關(guān)系展開(kāi)到線性就基本夠用了，稱為線性介質(zhì)。而這些線性介質(zhì)的本構(gòu)關(guān)系傳統(tǒng)上由介電常數(shù)ε和磁導(dǎo)率μ來(lái)刻畫(真空的介電常數(shù)和磁導(dǎo)率分別為ε0和μ0)。定義D=εE，B=μH，并由此得到P=(ε-ε0)E，M=

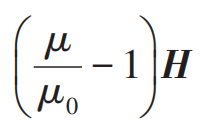
和如下“閔可夫斯基形式”的麥克斯韋方程組：

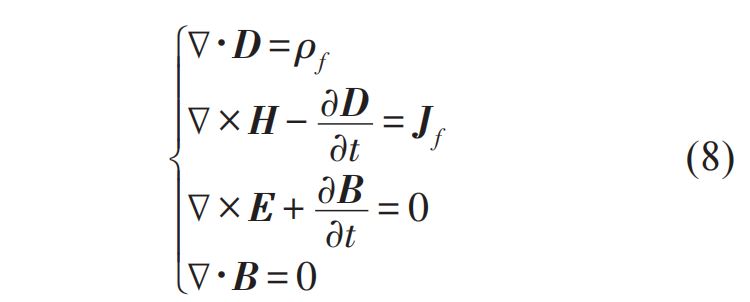
其中，ρf和Jf分別代表自由電荷/電流密度。前面已經(jīng)介紹過(guò)普適麥克斯韋方程組在洛倫茲變換下是協(xié)變的，即保持方程形式不變，只要把所有在方程里出現(xiàn)的量，包括場(chǎng)、時(shí)空坐標(biāo)和對(duì)時(shí)空坐標(biāo)的導(dǎo)數(shù)都從不帶撇的參照系換到帶撇的就行。那么動(dòng)體電動(dòng)力學(xué)方程如果是一道習(xí)題的話，它的題面是什么呢？在這里，我們把它嚴(yán)格地寫在下面。

動(dòng)體介質(zhì)電動(dòng)力學(xué)問(wèn)題：已知一種電磁介質(zhì)，其特性在靜止時(shí)由介電函數(shù)ε和磁導(dǎo)率μ來(lái)刻畫，求當(dāng)這塊介質(zhì)以勻速v相對(duì)于實(shí)驗(yàn)室參照系運(yùn)動(dòng)時(shí)所對(duì)應(yīng)的本構(gòu)關(guān)系。

接下來(lái)跟前面一樣，我們把實(shí)驗(yàn)室參照系記為S，把隨著介質(zhì)一起運(yùn)動(dòng)的參照系記為S′。由于在S′中介質(zhì)保持靜止，其電磁學(xué)特性由ε和μ來(lái)刻畫，為了解決上述動(dòng)體介質(zhì)電動(dòng)力學(xué)問(wèn)題，只要簡(jiǎn)單地做一個(gè)從S′系到S系的參照系變換就行。在近期的討論中，也有同學(xué)提出如果有多塊運(yùn)動(dòng)介質(zhì)怎么辦？其實(shí)這正是使用實(shí)驗(yàn)室參照系的優(yōu)勢(shì)，不管有多少塊介質(zhì)以不同的速度運(yùn)動(dòng)，都可以變換到唯一的實(shí)驗(yàn)室參考系來(lái)統(tǒng)一描述。下面，我們就用洛倫茲變換來(lái)解決這個(gè)問(wèn)題。從前面這個(gè)特殊例子，可以知道在洛倫茲變換下，電磁場(chǎng)E，B和源場(chǎng)電荷/電流密度ρ和J都必須跟著變，這里我們先給出嚴(yán)格的洛倫茲變換下場(chǎng)和源的正變換和逆變換形式：

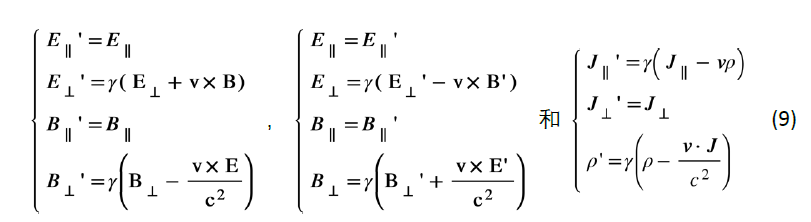
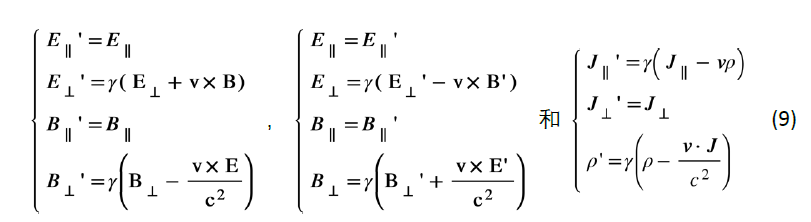
并且我們已知在S′系中的本構(gòu)關(guān)系為

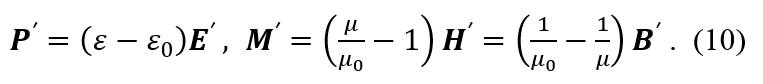
現(xiàn)在要求在S系中的電磁學(xué)方程。已經(jīng)知道，S系中電磁學(xué)方程的形式還是一樣的麥克斯韋方程組，唯一不清楚的就是S系里的本構(gòu)關(guān)系。這也很容易求，只要在洛倫茲變換下將S′系的P′和M′變換到S系的P和M就行了。下面就來(lái)求這個(gè)變換關(guān)系。先看電極化密度P。根據(jù)定義，體系里的極化分子貢獻(xiàn)的宏觀極化強(qiáng)度可以表達(dá)為

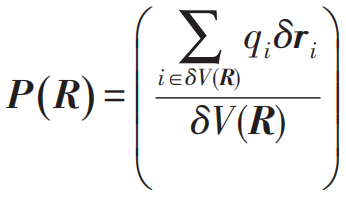
，其中δV(R)為空間坐標(biāo)R處的體積元，求和i遍歷該體積元內(nèi)的所有極性分子，δri代表第i個(gè)分子正負(fù)電荷中心之間的位移矢量。在S系中介質(zhì)中的極性分子以v的速度沿著x軸運(yùn)動(dòng)，而在S′系中則是靜止的，將我們?cè)谏弦还?jié)中對(duì)電荷密度的分析應(yīng)用于此，可以得到

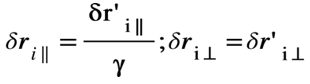
和

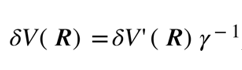
，由此可以得到這部分的貢獻(xiàn)在變換以后平行分量不變，而垂直分量要乘以一個(gè)γ因子。同時(shí)，在S系中除了上面考慮的極化分子會(huì)貢獻(xiàn)宏觀極化強(qiáng)度外，以速度v運(yùn)動(dòng)的分子電流也會(huì)對(duì)總極化強(qiáng)度產(chǎn)生額外的貢獻(xiàn)。這部分貢獻(xiàn)可以這樣計(jì)算。首先在S′系中與磁化強(qiáng)度M′(r′)對(duì)應(yīng)的分子電流為J′m=?′×M′(r′)，由上述電流/電荷密度變換關(guān)系，變換到S系以后會(huì)產(chǎn)生額外的電荷密度為

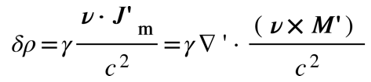
。由此，很容易證明這部分額外電荷密度分布對(duì)極化強(qiáng)度的貢獻(xiàn)為。將上述兩部分相加，得到S系中的電極化強(qiáng)度：

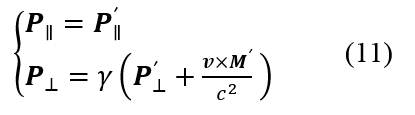
利用磁化強(qiáng)度與微觀分子電流之間的關(guān)系，我們可以類似地得到磁化強(qiáng)度在不同參照系之間的變換關(guān)系，這里不做詳細(xì)的推導(dǎo)，有興趣的讀者可以參考相關(guān)文獻(xiàn)[4]，最簡(jiǎn)潔漂亮的推導(dǎo)可以在泡利的Theory of Relativity中找到。與電極化強(qiáng)度類似，在S系中的磁化強(qiáng)度也有兩項(xiàng)貢獻(xiàn)，除了常規(guī)的分子電流帶來(lái)的磁化以外，運(yùn)動(dòng)介質(zhì)中電極化場(chǎng)的運(yùn)動(dòng)效應(yīng)也將帶來(lái)額外的貢獻(xiàn)，兩項(xiàng)相加可以得到：

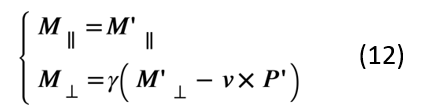
下一步，我們利用S′系中已知的靜態(tài)介質(zhì)本構(gòu)關(guān)系將P′和M′表示成E′和B′，然后再利用上述洛倫茲變換將E′和B′變換成E，B，最后將表達(dá)式里所有的γ都近似成1，就得到了精確到v/c一階的S系中的本構(gòu)關(guān)系如下[5]，

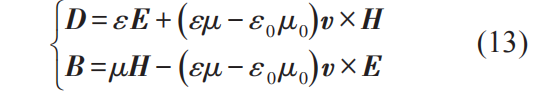
閔可夫斯基于1907年得到了上述方程。它的物理含義非常簡(jiǎn)潔明了，假設(shè)一塊介質(zhì)在靜止的時(shí)候可以用介電函數(shù)ε和磁導(dǎo)率μ來(lái)描述其電磁特性，那么當(dāng)它以速度v運(yùn)動(dòng)時(shí)，就成為了一塊具有“磁電”效應(yīng)的介質(zhì)，也就是說(shuō)磁場(chǎng)可以誘導(dǎo)出電極化，而電場(chǎng)也能誘導(dǎo)出磁極化，這種磁電耦合強(qiáng)度，與介質(zhì)和真空中的光速倒數(shù)平方之差成正比，也與介質(zhì)運(yùn)動(dòng)的速度v成正比。當(dāng)然，在這個(gè)簡(jiǎn)單的例子中，我們只討論了最簡(jiǎn)單的均勻線性介質(zhì)，在閔可夫斯基之后的一百多年時(shí)間里，又有不少文獻(xiàn)討論了各種更復(fù)雜的情況，比如非均勻介質(zhì)和包括變形和轉(zhuǎn)動(dòng)在內(nèi)的廣義運(yùn)動(dòng)介質(zhì)等。但無(wú)論是什么復(fù)雜的情況，麥克斯韋方程組的協(xié)變性都不會(huì)受介質(zhì)運(yùn)動(dòng)影響，運(yùn)動(dòng)介質(zhì)帶來(lái)的影響只能體現(xiàn)在本構(gòu)關(guān)系上，這是閔可夫斯基運(yùn)動(dòng)介質(zhì)電動(dòng)力學(xué)理論最精髓的所在。介質(zhì)運(yùn)動(dòng)帶來(lái)的最低階修正正比于介質(zhì)運(yùn)動(dòng)速度的一次方，完全是相對(duì)論效應(yīng)。

03什么是“伽利略電磁學(xué)”？

上面我們以如何求運(yùn)動(dòng)介質(zhì)的本構(gòu)關(guān)系為例，介紹了如何做洛倫茲變換的低速展開(kāi)，即嚴(yán)格按照洛倫茲變換的步驟，同時(shí)做電磁場(chǎng)、源場(chǎng)、時(shí)空坐標(biāo)、時(shí)空坐標(biāo)導(dǎo)數(shù)的變換，得到最后的表達(dá)式后，再對(duì)其中出現(xiàn)的所有v/c項(xiàng)做展開(kāi)到一階。在大多數(shù)情況下就是把其中出現(xiàn)的γ因子近似成1而已。在筆者看來(lái)，這樣的展開(kāi)毫無(wú)必要，因?yàn)槟呐虏蛔鋈魏谓疲鍌惼澴儞Q就已經(jīng)是線性變換了，足夠簡(jiǎn)單了。在這個(gè)計(jì)算資源豐富的時(shí)代，做這點(diǎn)近似帶來(lái)的變化無(wú)非是寫程序的時(shí)候?qū)懸恍羞€是兩行，按計(jì)算器的時(shí)候按三下還是五下的區(qū)別。當(dāng)然，做了近似以后，在解析表達(dá)式上我們可以用統(tǒng)一的矢量方程描寫，不必把平行和垂直分量分開(kāi)寫，看起來(lái)會(huì)簡(jiǎn)潔一些。然而在歷史上，還有一種在洛倫茲變換線性展開(kāi)的基礎(chǔ)上，針對(duì)不同的具體問(wèn)題對(duì)場(chǎng)量再做進(jìn)一步近似的方法，稱為“伽利略電磁學(xué)”[6]，下面我們?cè)俸?jiǎn)單介紹一下這種近似方法和伽利略變換的關(guān)系。

簡(jiǎn)單地說(shuō)，這種“伽利略電磁學(xué)”其實(shí)就是我們熟悉的準(zhǔn)靜態(tài)近似，即在某些特殊情況下，可以把動(dòng)態(tài)的電磁學(xué)問(wèn)題近似成靜電學(xué)或者靜磁學(xué)問(wèn)題。相應(yīng)的，準(zhǔn)靜態(tài)近似也有兩種，分別對(duì)應(yīng)靜電學(xué)和靜磁學(xué)問(wèn)題，稱為電極限和磁極限。對(duì)于電極限準(zhǔn)靜態(tài)近似或者“電學(xué)伽利略電磁學(xué)”來(lái)說(shuō)，這類問(wèn)題主要是研究與時(shí)間緩變電荷密度相關(guān)的電磁學(xué)問(wèn)題。在這種情況下，我們可以把其中的縱向電場(chǎng)和電荷密度看作零階量，磁場(chǎng)強(qiáng)度和電流密度看作一階小量，而電場(chǎng)的橫向分量則作為二階小量被忽略掉。這樣的電場(chǎng)就是無(wú)旋場(chǎng)，可以寫作某個(gè)標(biāo)量勢(shì)的梯度，E(r,t)=?φ(r,t)，并且t時(shí)刻的標(biāo)量勢(shì)場(chǎng)φ(r,t)可以由同一時(shí)刻t的電荷密度分布ρ(r,t)通過(guò)解泊松方程來(lái)確定，相應(yīng)的磁場(chǎng)則由安培定律來(lái)確定，總結(jié)如下：

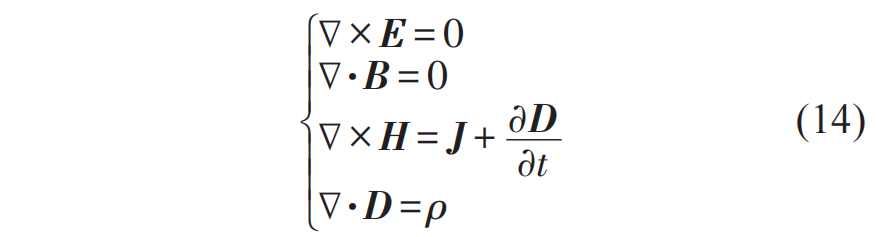
類似的，還有另一類電磁學(xué)問(wèn)題是與隨時(shí)間緩變的電流分布相關(guān)，在這類問(wèn)題中，可以把磁場(chǎng)強(qiáng)度和電流密度看作零階量，把橫向電場(chǎng)看作一階小量，而把電荷密度與電場(chǎng)這兩者隨時(shí)間的變化率看作二階小量予以忽略(等價(jià)于問(wèn)題中電流密度的散度為零)。這種近似就是磁極限準(zhǔn)靜態(tài)近似或者“磁學(xué)伽利略電磁學(xué)”，使得我們可以在安培定律中忽略掉位移電流的貢獻(xiàn)。在這種近似中，t時(shí)刻的磁場(chǎng)強(qiáng)度H(t)完全由同一時(shí)刻t的無(wú)散度電流分布J(r,t)通過(guò)解瞬時(shí)靜磁學(xué)問(wèn)題來(lái)得到，磁極限準(zhǔn)靜態(tài)近似下的麥克斯韋方程組如下：

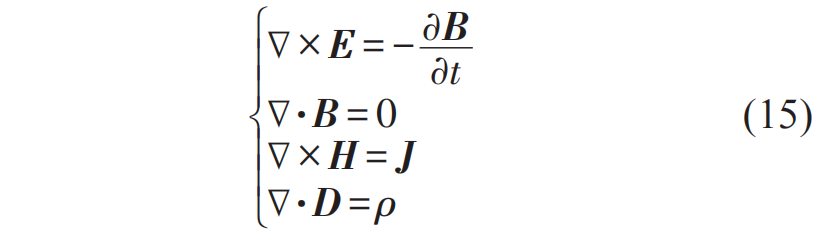
在凝聚態(tài)物理中，求解金屬中等離激元(plasmon)的方程就是典型的“電學(xué)伽利略電磁學(xué)”，而求解超導(dǎo)體中磁通運(yùn)動(dòng)的方程則是典型的“磁學(xué)伽利略電磁學(xué)”。 那么現(xiàn)在問(wèn)題來(lái)了，上述兩套準(zhǔn)靜態(tài)極限下的近似方程滿足伽利略變換嗎？關(guān)于這個(gè)問(wèn)題的討論，在20世紀(jì)的許多文獻(xiàn)里是非常混亂的。在我們給出明確的回答之前首先要澄清一下這些問(wèn)題，即“當(dāng)我們?cè)谡f(shuō)某個(gè)方程組滿足伽利略變換的時(shí)候，我們到底在說(shuō)什么”？在許多文獻(xiàn)[7，8]里，作者實(shí)際上是在說(shuō)這樣一個(gè)邏輯過(guò)程。第一步，對(duì)時(shí)空坐標(biāo)做伽利略變換，然后問(wèn)需要對(duì)電磁場(chǎng)和源場(chǎng)做什么樣的相應(yīng)變換可以保持變換后的方程形式不變，通過(guò)這一條件得到場(chǎng)和源的變換關(guān)系。這么做其實(shí)是在反推洛倫茲變換中場(chǎng)和源的變換方式在滿足上述準(zhǔn)靜態(tài)條件時(shí)的近似形式。但問(wèn)題是源場(chǎng)，也就是電荷密度和電流密度，可以由微觀帶電粒子的坐標(biāo)和運(yùn)動(dòng)速度完全確定，所以它們的變換形式是可以通過(guò)伽利略變換直接得到的，不必通過(guò)電磁學(xué)方程不變這個(gè)條件反推。那么，只有通過(guò)上述過(guò)程反推出來(lái)的電荷密度和電流密度的變換形式與伽利略變換直接得到的一致，才可以說(shuō)這樣的近似方程組滿足伽利略變換，如果不一致則說(shuō)明這里面有不自洽之處，源的變換關(guān)系不能通過(guò)伽利略變換得到。 先來(lái)看電極限的準(zhǔn)靜態(tài)方程組在伽利略變換下的行為，相關(guān)綜述文獻(xiàn)[9]中給出如果要求電極限的準(zhǔn)靜態(tài)方程組在伽利略變換下不變，在做時(shí)空坐標(biāo)變換的同時(shí)，場(chǎng)和源必須同時(shí)做如下變換，

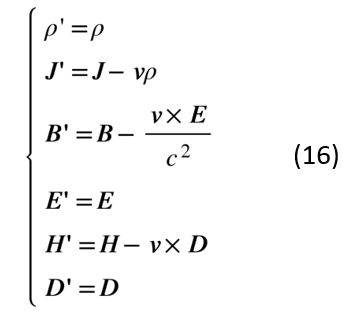
從中我們可以看出電荷密度和電流密度的變換關(guān)系與通過(guò)伽利略變換直接得到的完全一致，因此電極限下的準(zhǔn)靜態(tài)方程組的確滿足伽利略變換。這在物理上也很好理解，在這組方程下t時(shí)刻的電磁場(chǎng)完全由同時(shí)刻下的電荷密度分布ρ(r,t)和電流密度分布J(r,t)決定，電磁場(chǎng)自身獨(dú)立的動(dòng)力學(xué)特征被完全忽略以至于成為物質(zhì)場(chǎng)ρ(r,t)和J(r,t)的“附屬場(chǎng)”，從而滿足伽利略變換。

對(duì)于磁極限下的準(zhǔn)靜態(tài)方程，綜述文獻(xiàn)中也給出了場(chǎng)和源的變換關(guān)系如下。 如果要求磁極限的準(zhǔn)靜態(tài)方程組在伽利略變換下不變，在做時(shí)空坐標(biāo)變換的同時(shí)，

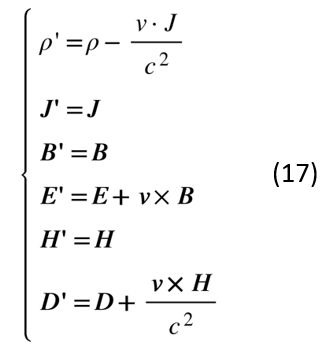
很明顯，這里要求的源場(chǎng)，即電荷密度和電流密度的變換關(guān)系完全不能由伽利略變換直接得到。因此，磁極限準(zhǔn)靜態(tài)近似下的變換關(guān)系不能看作是跟伽利略變換自洽的，事實(shí)上它只能通過(guò)對(duì)洛倫茲變換做低速展開(kāi)，并忽略掉上述情況下場(chǎng)量的高階小量才能得到。這一有趣的電和磁的不對(duì)稱性是有其深刻物理含義的，偉大的物理學(xué)家費(fèi)曼在其《費(fèi)曼物理學(xué)講義》第二卷第一章中系統(tǒng)地闡述了這種電磁不對(duì)稱性，并指出磁現(xiàn)象在本質(zhì)上是完全相對(duì)論性的，不存在“非相對(duì)論磁學(xué)”，我們擬另文專門展開(kāi)討論這一問(wèn)題。另外，我們還要指出一點(diǎn)，無(wú)論是電極限還是磁極限下的“伽利略電磁學(xué)”，本質(zhì)上都是在某些特殊條件下徹底忽略電磁場(chǎng)自身的動(dòng)力學(xué)，而不是對(duì)電磁場(chǎng)動(dòng)力學(xué)去做各種錯(cuò)誤的“近似”。最后，利用變換(16)和(17)，讀者可以自己再去做一遍上文中運(yùn)動(dòng)介質(zhì)中的電動(dòng)力學(xué)問(wèn)題，會(huì)發(fā)現(xiàn)得到的結(jié)果與正確的閔可夫斯基形式(13)并不一致，這也是由于在“伽利略電磁學(xué)”中忽略電磁場(chǎng)動(dòng)力學(xué)所導(dǎo)致的。

審核編輯：郭婷