本文將向大家介紹一種在科學研究中非常重要和有趣的計算方法——蒙特卡洛方法,這種方法在數學、物理學、化學、工程、經濟學、環境動力學等多個領域都有廣泛的應用。
到底什么是蒙特卡洛方法?我們可以先從它的名字開始了解,蒙特卡洛(Monte Carlo)是摩納哥公國的一座城市,是世界著名的“賭城”。以“蒙特卡洛”來命名這種計算方法就是因為其本身便是一種概率算法,其核心思路是通過概率實驗所求的概率來計算我們感興趣的一個量。
概率算法的1.0版
為了更好地理解蒙特卡洛方法,我們先簡單了解一下“蒲豐投針問題”,這個問題的提出被認為是蒙特卡洛方法的起源。 18世紀,法國數學家蒲豐提出了一種計算圓周率π的方法——隨機投針法:假設我們有一個以平行且等距為a的木紋鋪成的地板,隨意拋一支長度為l(比木紋之間距離小)的針,通過針和其中一條木紋相交的概率p,即可計算圓周率π。計算公式為:
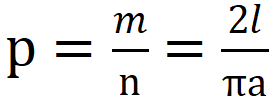
,其中n是投針的總次數,m是針與平行直線交點的總數目。

圖 蒲豐投針問題示意圖
這個方法的原理可以通過概率學的推導計算來進行證明。由于投針掉落的位置與方向都是隨機且獨立的。我們假定落地后針的中心距最近的地板條紋的距離為X,那么X在[0,a/2]上均勻分布;針與地板條紋的夾角為Y,則Y在[0, π/2]之間均勻分布。當
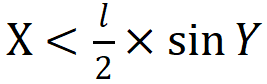
時,針與木紋相交,因此(X,Y)的概率密度函數和相交的概率P分別為:
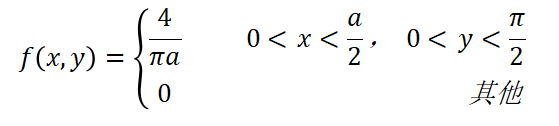
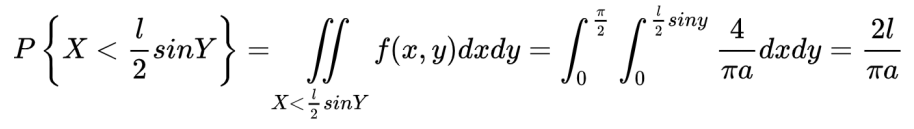
相信大家都聽懂了,下面我們可以…… 好吧,這里還有一種雖然不夠嚴謹、但易于理解的解釋: 我們想象一個長度為πa的鐵絲,被繞成了一個直徑為a的圓環。那么無論我們怎么扔這個鐵環,它與條紋的交點恒為兩個,因此當投針n次后,相交的次數恒為2n。如果我們把鐵絲拉直再扔,這樣的鐵絲扔下時與平行線相交的情形要比圓圈復雜些,可能有4個交點、3個交點、2個交點、1個交點,甚至于都不相交。由于圓圈和直桿的長度同為πa,根據機會均等的原理,投擲n次,直桿與平行線組交點的總數期望也是2n。同時還有一個規律,當投針次數n固定時,鐵絲的長度l與交點總數m應為正比關系,即m=kl。考慮到l=πa時,m=2n,將
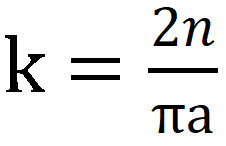
代入前式可得:
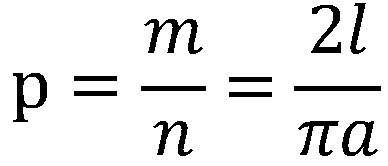
。 投針試驗既然是依靠概率的算法,那么隨著投針次數越來越多,計算求得的π值也會越來越接近于真實值。下表給出了一些比較出名的投針試驗得到的圓周率估計值,可以看到在投擲數千次后,計算得到的圓周率與我們所熟知的π值的誤差仍較大。
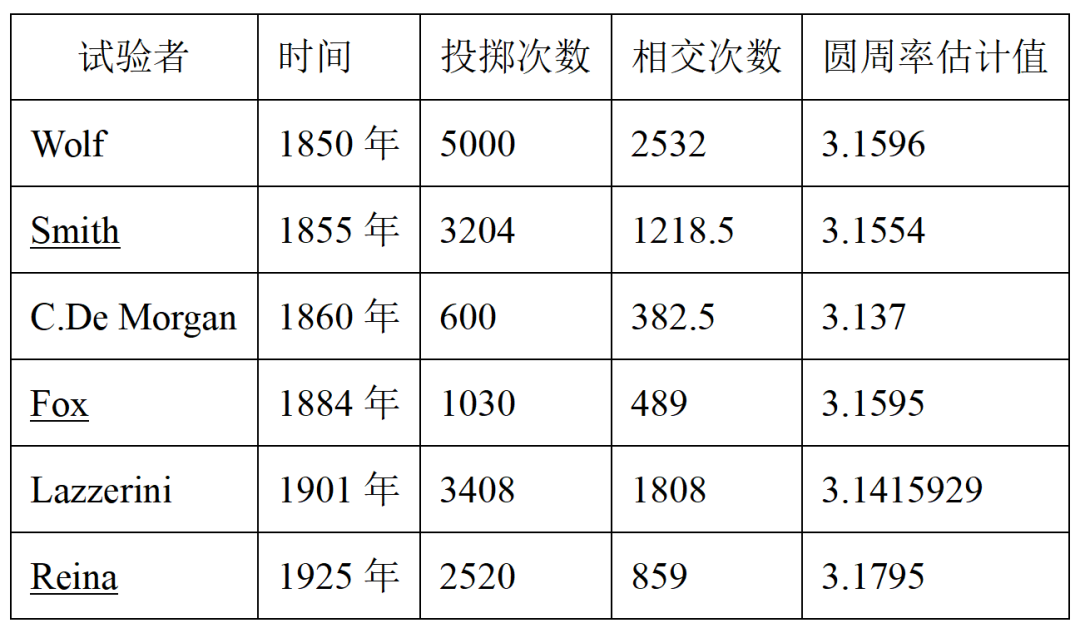
表 一些投針試驗的計算結果
1995年,馬修斯發表了他如何通過觀察天空中亮星的分布計算圓周率。他的試驗方法基于一個基本的原理:任意兩個自然數互質的概率為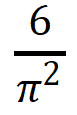 。他從眾多星星中選擇100個亮星,將這些亮星兩個分成一對,然后計算每對星之間的角距,得出一堆數據,然后檢查這些數據的因子情況,從中計算出π值約為3.12772。
。他從眾多星星中選擇100個亮星,將這些亮星兩個分成一對,然后計算每對星之間的角距,得出一堆數據,然后檢查這些數據的因子情況,從中計算出π值約為3.12772。
從上述兩個例子來看,依靠重復的物理、觀測等試驗行為來獲取隨機性數據的方法往往很難得到令人滿意的計算結果,這主要是受到了樣本數量的限制。而早在魏晉時,我國的劉徽便通過割圓術求得了π的近似值3.1416。
“史詩級加強”X.0版
20世紀40年代,美國“曼哈頓計劃”的成員S.M.烏拉姆和J·馮·諾伊曼第一次把這種通過概率事件來計算關注的確定值的方法命名為“蒙特卡洛方法”。隨著電子計算機的發明和科學技術的發展,蒙特卡洛方法得到了“史詩級加強”。

圖 S.M.烏拉姆(左)和J·馮·諾伊曼(右)
計算機在進行蒙特卡洛模擬的過程中獲取隨機性最根本的方法是通過固定算法得到符合[0,1]均勻分布的“偽隨機數”,它并不真正的隨機,但具有類似于隨機數的統計特征,如均勻性、獨立性等。
這里介紹另一種計算π值的蒙特卡洛方法——“撒豆法”。該方法假定有無數個豆子被均勻地撒在下圖所示的正方形中,那么落在圓內的豆子數m與落在正方形內的豆子總數n的比值的期望應與它們面積的比值一致,即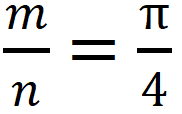 ,這樣就可以計算得到π的值。
,這樣就可以計算得到π的值。

圖 “撒豆法”求解π值模型示意圖
利用計算機開展上述計算,僅需不到一分鐘的時間,便可以完成十億次“撒豆”,并得到相應的計算結果。計算的python代碼及運行結果見下圖。
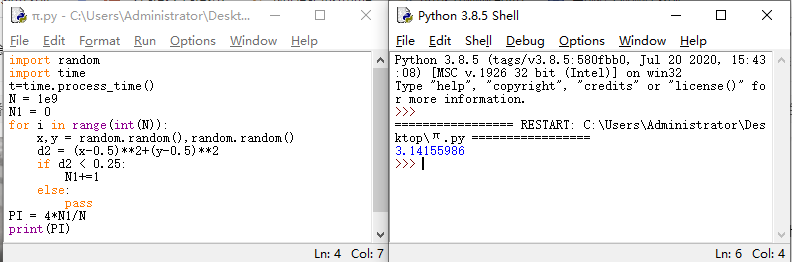
圖 計算所用python代碼及計算結果
計算機時代的蒙特卡洛模擬無疑具有超高的計算效率,且其計算效率隨著計算機技術的飛速發展而不斷提升。
核科學領域中的應用
蒙特卡洛方法在核科學領域中有著廣泛的應用。核物理領域的基本參數(如反應截面、散射發射角度分布、能譜分布、衰變、衰減等)主要來自核物理實驗及理論模型等,而蒙特卡洛模擬程序也在與核物理實驗、理論模型等的相互參照、驗證和迭代更新中不斷發展至今。
如今在核物理領域有許多廣泛使用的蒙特卡洛程序,如FLUKA、MCNP、PHITS、GEANT4等,這些蒙特卡洛程序對核物理學的發展至關重要,同時它們的運用過程也非常的有趣和巧妙。
具體以加速器輻射防護領域為例,粒子加速器產生的高速運動的微觀粒子(一般每秒可達上億個粒子)在與其他物質碰撞時,會通過核反應產生帶電粒子、中子、γ射線等次級輻射,這些次級輻射又會繼續與材料發生核反應,產生更多的次級輻射。如此周而復始,其反應過程非常復雜,無法通過人力模擬計算。而蒙特卡洛方法,正好能夠解決這個難題。
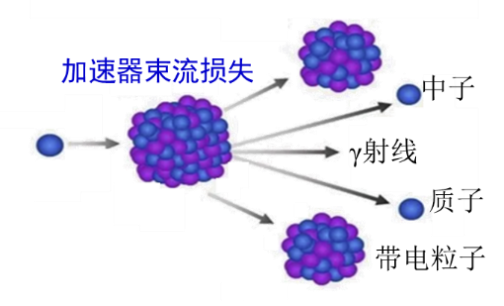
圖 加速器產生電離輻射示意圖
為了使加速器產生的強電離輻射降低到可接受的低水平,科研人員需要對次級粒子的輸運過程進行仿真模擬,并根據模擬結果進行屏蔽阻擋設計。
接下來我們以一個簡單模型為例,介紹蒙特卡洛方法應用于粒子輸運模擬的基本思路。如下圖所示,假定在一個二維的矩形屏蔽中,充滿了物質B,左、上、下側設置黑色隔板,右側設置紅色隔板。

圖 模型示意圖
假設粒子A具有以下特質:
粒子A在物質B中直線運動。但每直線前進1m,就會停止前進并與B發生反應,反應后繼續直線前進。反應有三種可能:
①:A忽略與B的反應,繼續按原方向前進1m,發生概率為1/3;
②:A與B發生正碰撞,向左偏轉45°前進1m,發生概率為1/3;
③:A與B發生反碰撞,向右偏轉45°前進1m,發生概率為1/3。
2. 當A碰到黑色隔板后,會立刻消失;
3. 當A碰到紅色隔板后,會進入環境。 如果我們想知道當大量粒子A從上圖中P位置向右水平射出,會有多少個粒子通過紅色隔板進入環境,就可以利用蒙特卡洛程序進行大量模擬。 對單個事例,當粒子A從P點出發前進1米后,抽取偽隨機數N為[0,1]的均勻分布,根據抽取的數字決定其下一步的運動軌跡:當0
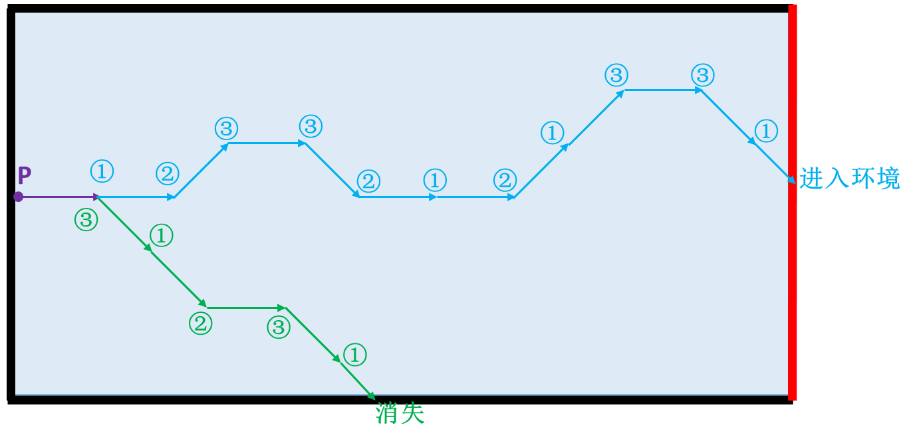
下圖給出了粒子A可能的兩種運行軌跡,利用計算機程序可以高效地完成大量的粒子模擬,得到計算結果。根據統計學特性,計算的事例越多,結果也就越接近期望值。
圖 粒子A可能的兩種運行軌跡
在理解了上述示例的計算思路后,不難想象在輻射防護領域的研究中,只要我們知道了粒子在運行過程中每一步可能發生的反應類型及其概率等基本的核物理參數,就可以通過計算機程序實現各種不同情形的模擬計算。
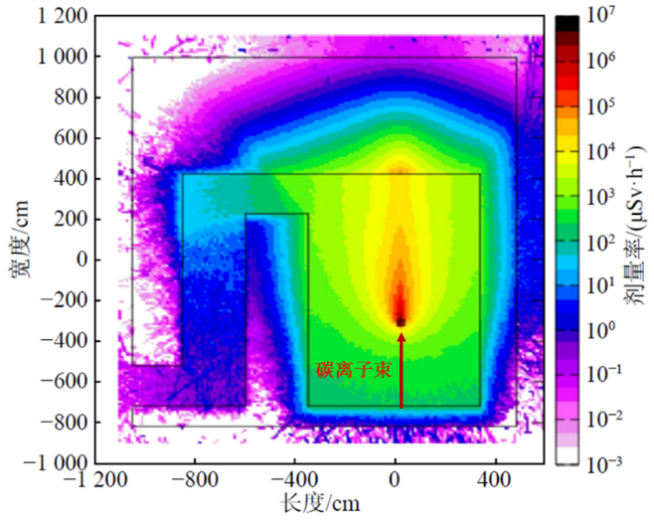
比如FLUKA程序可被用于計算國內醫用重離子加速器HIMM治療室的輻射劑量率分布。如下圖所示,可以看出碳離子集中損失的位置輻射劑量率最高,約為106μSv/h;而經過混凝土屏蔽后,屏蔽外的輻射劑量率衰減到了2.5μSv/h以下。
圖 HIMM治療室劑量率分布圖。HIMM裝置每秒鐘能夠產生1億個最高能量為400MeV/u的碳離子束用于治療,束流照射人體時幾乎全部損失,從而產生各種次級輻射。
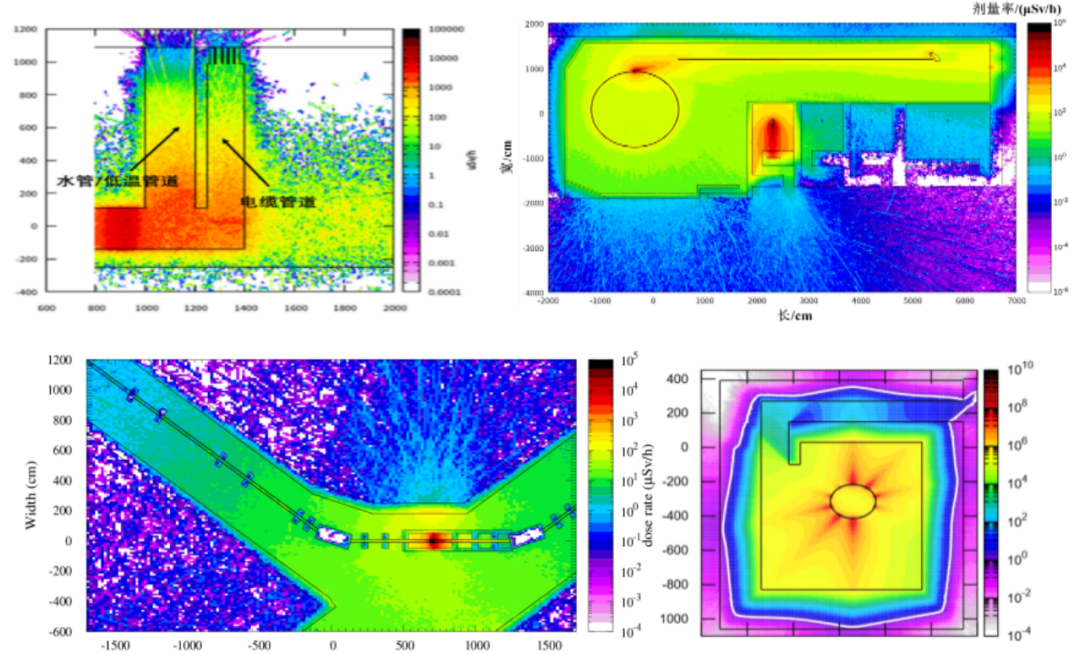
利用FLUKA程序,還可以開展更為復雜的輻射防護模擬研究,如更加多樣的束流損失模式、更多的粒子種類與能量、更加復雜的建筑結構等。
圖 各類加速器輻射劑量分布圖示例
讀到這里,相信大家對蒙特卡洛方法已經有了一個基本的了解。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4615瀏覽量
92980 -
蒙特卡洛
+關注
關注
0文章
13瀏覽量
8178
原文標題:有趣的“賭博算法”——蒙特卡洛方法
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
電阻器的工作原理與計算方法
波特率的定義和計算方法 波特率與數據傳輸速度的關系
FPGA門數的計算方法
為什么高UVLO對于IGBT和SiC MOSFET電源開關的安全工作非常重要

電流計算方法與配線法的區別
電荷放大電路的帶寬 和IV轉換電路帶寬計算方法不一樣嗎?
DCS系統I/O點數計算方法與原則
相電流和線電流的關系計算方法
機器學習中的交叉驗證方法
儲能容量的計算方法
電壓探頭延遲計算方法及應用

電線安全載流量的計算方法
耐壓測試中漏電流的計算方法




 非常重要和有趣的計算方法——蒙特卡洛方法
非常重要和有趣的計算方法——蒙特卡洛方法











評論