相機畸變是影響相機標定精度的關鍵因素。由于畸變補償不準確，傳統的標定方法不能滿足要求較高標定精度的測量系統的要求。本文提出了一種基于迭代畸變補償算法的新型相機標定方法。相機的初始參數由全場相機像素和相位標靶上的相應點進行標定。提出了一種補償畸變的迭代算法。為了提高相位標靶的精度，還提出了一種二維擬合和插值的方法。與傳統的標定方法相比，該方法不依賴于畸變數學模型，并且在復雜的畸變條件下是穩定

1 引言

相機標定是光學三維測量的第一步，也是最重要的一步，如立體視覺、條紋投影技術和偏度測量。一般有兩個方面影響照相機標定的精度。一是所選相機模型的準確性。另一個是特征點在世界坐標系的定位精度。相機畸變是影響相機模型精度的關鍵因素。針孔模型通常用于描述一般的成像過程，它是世界上的一個三維點與相機中相應的二維圖像之間的線性投影。然而，由于相機的畸變，真實的成像過程是一個非線性投影。相機鏡頭畸變可分為徑向畸變、偏心畸變和薄棱鏡畸變。通常采用基于參數的方法來補償透鏡畸變。Alvarez等人提出了一個數學模型來研究變焦鏡頭的畸變變化。桑塔納-Cedres等人研究了通過最小化線重投影誤差來估計畸變模型。傳統的標定方法使用帶有畸變參數的無限高階多項式來表示由不同源引起的畸變。首先對初始畸變參數進行估計，然后采用基于最小二乘法的優化算法對其他攝像機參數的畸變參數進行優化。由于輸入的精度對迭代優化的嚴格性起著重要的作用，因此攝像機標定的精度高度依賴于初始畸變參數的精度。此外，真實的畸變是由于復雜鏡頭系統的累積效應、相機幾何誤差和圖像傳感器的不完美形狀的結果；因此，需要一個具有足夠參數的模型來模擬任何可能的畸變。然而，流行的常規標定只需要采用具有徑向畸變和偏心畸變的部分偏真參數的畸真模型；實驗表明，一個更精細的模型將不會幫助提高精度，但也會導致數值不穩定性。因此，傳統方法的應用畸變數學模型不能完全匹配實際畸變，也限制了標定精度。為了解決這一問題，研究了非參數畸變補償方法。Thirthala［16］等人提出了一種利用多焦張量恢復徑向畸變的方法；然而，這種方法是基于畸變中心在圖像中心的假設，這通常不是一個可靠的假設。Hartley等人提出了一種只考慮徑向畸真的無參數標定方法。Ryusuke等人提出了一種利用二元結構光補償鏡頭畸變的方法，但該方法不能標定相機的內參。因此，需要研究一種靈活、穩定的方法來標定相機的內部參數、外部參數和畸變。

通常，使用一組具有已知世界坐標的二維或三維控制點或特征點作為標定過程的輸入數據。與3D靶標相比，棋盤格、平面上的正方形和圓形等二維圖案被頻繁使用，因為它們易于制造和處理。近年來，一種二維相位靶標由于其高精度的特征檢測、大量任意提供控制點和全自動過程等優點而被研究為傳統平面靶標的替代品［21，22］。Xue等人提出了一種基于同心圓光柵和楔形光柵正交消失點標定的相機標定方法［23］。Liu等人引入了交叉條紋圖案作為相機標定的模型平面。Ma等提出了一種以條紋圖案組作為標定靶標的特征提取方法。此外，由于從正弦條紋中獲得的相位對失焦圖像［26，27］的影響較小，因此相位靶標可以有效地標定對焦深度小、工作距離長的相機。Schmalz等將相位靶標與經典平面靶標進行了比較，以顯示相位靶標的優越性。

為了提高標定精度，研究了減小相位靶標定位誤差的方法。Schmalz等人［21］提出了一種基于四個相鄰像素的平滑相位值的擬合方法。Huang等［22］應用加窗多項式擬合技術對相位靶標進行了優化，并將結果與線性插值、雙二次擬合和雙二次擬合進行了比較。關于原理和計算過程的細節很少。實驗采用窗口大小為200×200像素的窗口雙邊緣擬合。然而，并沒有提供選擇窗口大小的原因以及窗口大小對結果的影響程度。雖然實現了顯著的重投影精度，但窗口大小的可行性仍需進行討論。上述技術主要研究了標定靶標的設計和特征檢測定位精度的提高。然而，目前還沒有關于提高相機畸變的補償精度和優化具有相位靶標的相機模型的研究。

本文提出了一種基于迭代畸變補償算法的新型相機標定方法。利用全場攝像機像素和相位靶標上的相應點來計算標定參數。可以得到基于線性投影的真實像素與重投影像素之間的畸變所引起的偏差。通過補償偏差，可以得到一個像素的校正坐標。利用黎文伯格-馬夸特算法，通過最小化校正后的坐標和重投影像素之間的差值，迭代優化標定參數。為了提高世界坐標的定位精度，提出了擬合技術和應用于相位靶標的窗口大小的可行性，以補償任何相位誤差。

02 原理和方法

2.1 相位靶標

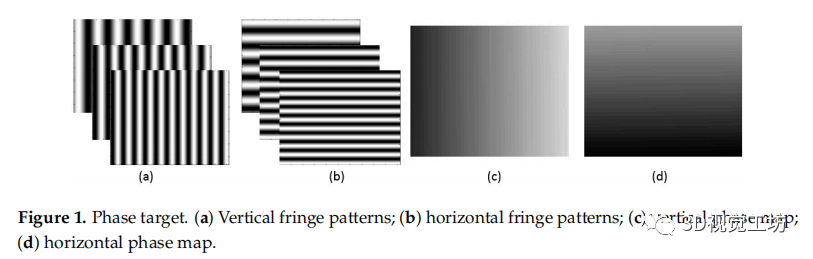
圖1 相位靶標；（a） 垂直條紋圖案；（b） 水平條紋圖案; （c） 垂直相位圖; （d） 水平相位圖。

本文使用了一個相位靶標來輔助本文提出的標定方法（如圖1所示）。除了在引言中所述的相位靶標的優點外，使用相位靶標的主要原因是它是一個密集和連續的靶標，并且滿足了所提出的畸變補償算法的要求。所提出的畸變補償方法需要計算真實像素與重投影像素之間的偏差。當使用相位靶標時，攝像機像素可以根據連續的相位圖，根據不同的標定姿態找到相應的世界點。雖然使用了傳統的二維標定板（如棋盤），但由于相同的相機像素由于特征點有限且離散，無法發現不同標定姿態中的相應世界點，因此所提出的標定方法將會失敗。兩組相互垂直的移相條紋圖案按順序顯示在液晶顯示器（LCD）屏幕上，這些顯示的圖案由照相機從不同的視點捕捉到。在應用相移法和相位展開法［28–30］后，得到了兩個相互垂直的絕對相位圖，如圖1所示。如果已知LCD像素間距的大小 和每個條紋周期的LCD像素數 ，則一個攝像機像素可以根據公式（1）和（2）的相位值唯一地定位其在世界坐標系中的相應的物理位置。

2.2 基于迭代畸變補償算法的標定

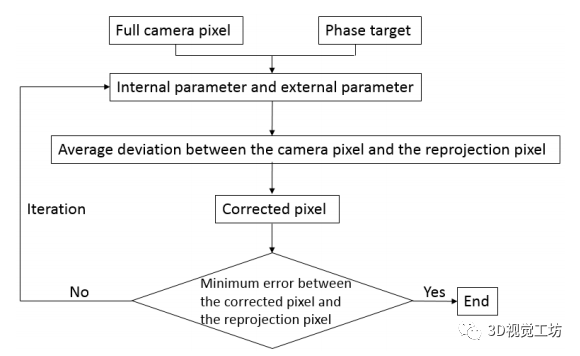
圖2 我們方法的標定過程

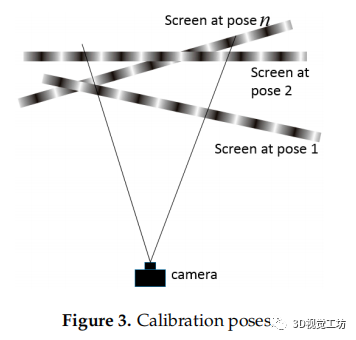
圖3 標定姿勢

所提出的相機標定過程如圖2所示。兩組正交條紋圖案依次顯示在液晶屏幕上。兩組正交條紋圖案依次顯示在液晶屏幕上。在整個標定過程中，會捕獲任意 幅LCD姿態的圖像，如圖3所示。根據每個LCD姿態，選擇在CCD（電荷耦合器件）平面上均勻分布的 k 個攝像機像素，對其進行參數標定。所選的像素可以是全像素，也可以是具有相同間隙的采樣像素，以提高計算速度。根據公式（1）和（2）的相位值得到相應的世界坐標。根據方程（3），可以得到一個線性投影 ：

其中是相機像素坐標， 是對應的世界坐標。A是照相機的內參， 是相機主點， 是圖像在 方向的縮放系數。 是剛體變換矩陣從世界坐標系到相機坐標系。讓我們用 表示旋轉矩陣 的第 列，用 表示線性投影 的第 列。對于已知的 、 是正交的，可以得到對內部參數的兩個約束條件：

由于一個標定姿態可以根據公式（4）提供兩個約束條件，因此內部參數A可以從至少三個姿態中計算出來。一旦已知A，外部參數 可以根據公式（5）計算：

在線性投影模型下，對于一個相機像素 ，畸變會導致真實坐標和重投影 的偏差：

其中： 是像素點 的相應世界坐標。由于畸變對于固定焦距的鏡頭和短工作距離的相機是系統誤差，因此對于不同標定姿態的偏差應該是固定值。通過根據公式7使用 個位姿的平均偏差來補償畸變，校正后的坐標 可以得到精確匹配的線性模型：

直到現在，內參A的初始值，外參 和外參 ，和畸變偏差 ，然后通過迭代循環重新計算和優化，用黎文堡-馬夸特算法最小化以下函數：

2.3 相位標靶誤差補償算法

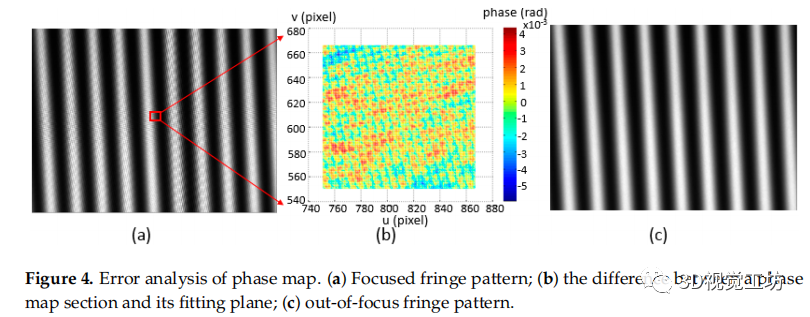
圖4 相位圖的誤差分析。（a）聚焦條紋圖案；（b）表示相位圖截面與其擬合平面之間的差值；（c）離焦條紋圖案。

當相位靶標放置在相機的聚焦深度時，捕獲的條紋圖案出現可觀察的變形，如圖4a所示。變形來自于液晶屏幕上記錄的像素網格，以及由相機像素和液晶像素之間的干涉所產生的摩爾條紋。取計算得到的相位圖中間的一個小區域，從相位值與其擬合平面的差值可以看出影響，如圖4b所示。為了提高相位靶標的定位精度，保證后續標定過程的適當輸入，研究了一種噪聲補償算法來對相位靶標進行細化。作為［19］中使用的虛擬散焦技術，可以應用于捕獲的條紋模式。然而，很難確定過濾器的大小。消除這種影響的一種靈活的方法是，通過移動靶標位置或調整相機的對焦，將相位靶標定位在相機的失焦位置，如圖4c所示。

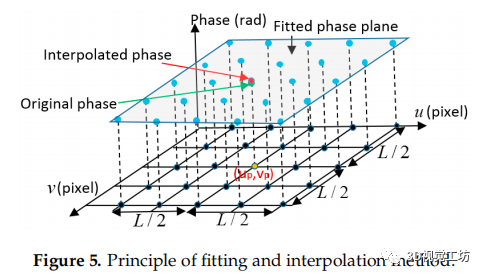
圖5 擬合原理和插值方法。

由于理論上得到的絕對相位圖是連續且光滑的，因此可以采用擬合和插值的方法對相位數據進行平滑處理，如圖5所示。對于如圖5所示的相機像素，其原始相位用圖5所示的綠點表示。在相面上的點附近，相面和切面之間只有一個很小的差異。因此，可以使用最小二乘算法將一個相位平面（如圖5中所示的灰色平面）與相鄰的L/2像素的相位值（藍點）進行擬合。在擬合平面的基礎上，根據基于三次多項式插值的擬合平面對原始相位進行平滑，可以計算出插值的相位值（紅點）。使用更大的擬合窗口（L）可以更有效地消除誤差，提高相位數據的精度。但根據方程（1）-（3），得到的相圖與相機像素坐標（u，v）之間的關系可以通過方程（9）和（10）得到，它們不是線性方程，因此捕獲的相圖是一個曲線曲面。

其中是 的逆矩陣的元素。因此，如果應用的窗口太大，窗口中的斜率數據會有明顯的變化，計算點的調整會不準確。

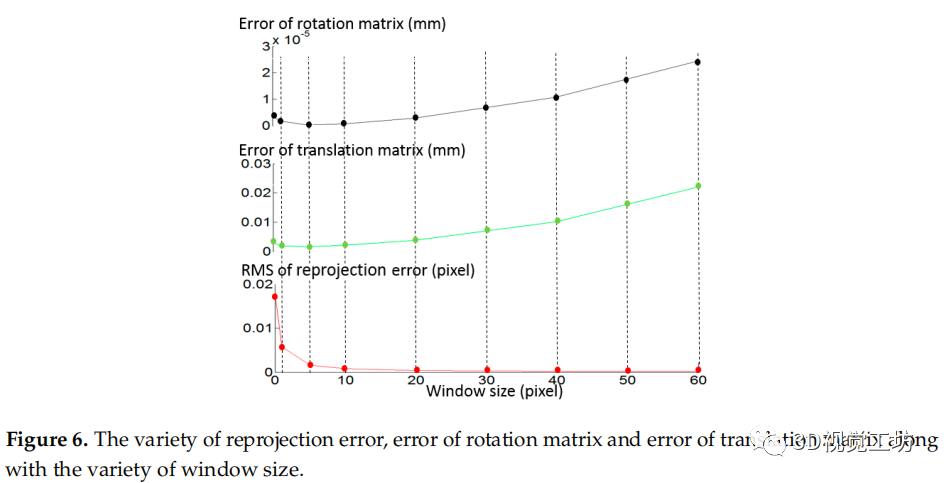
圖6 重投影誤差的變化、旋轉矩陣的誤差和平移矩陣的誤差以及窗口大小的變化。

為了優化擬合窗口的大小，我們進行了一個仿真實驗，如圖6所示。隨機相位誤差是仿真過程中唯一的誤差源。隨著窗口大小從0（沒有應用擬合和插值）增加到5個像素，重投影誤差的均方根（均方根）顯著降低（如紅線所示）。在這個過程中，旋轉矩陣R的誤差和平移矩陣t的誤差也都減少了（分別由黑線和綠線所示）。然而，當窗口大小從5像素增加到60像素時，雖然重投影誤差的RMS從0.0016像素降低到0.000172像素，但旋轉矩陣和平移矩陣的誤差都增加了。仿真結果表明，5個像素是一個合適的擬合窗口大小，可以降低相位噪聲，且不會過度調整原始相位值。

03 實驗結果和討論

3.1 仿真研究

仿真驗證了所提出的非參數畸變補償方法。模擬相機圖像的大小為 ，主點在像素 處， 軸的尺度系數分別為3543、3522像素。徑向畸變 ，偏心畸變（），薄棱鏡畸變 通過公式11獲取，其中、，畸變的中心為： 像素點。

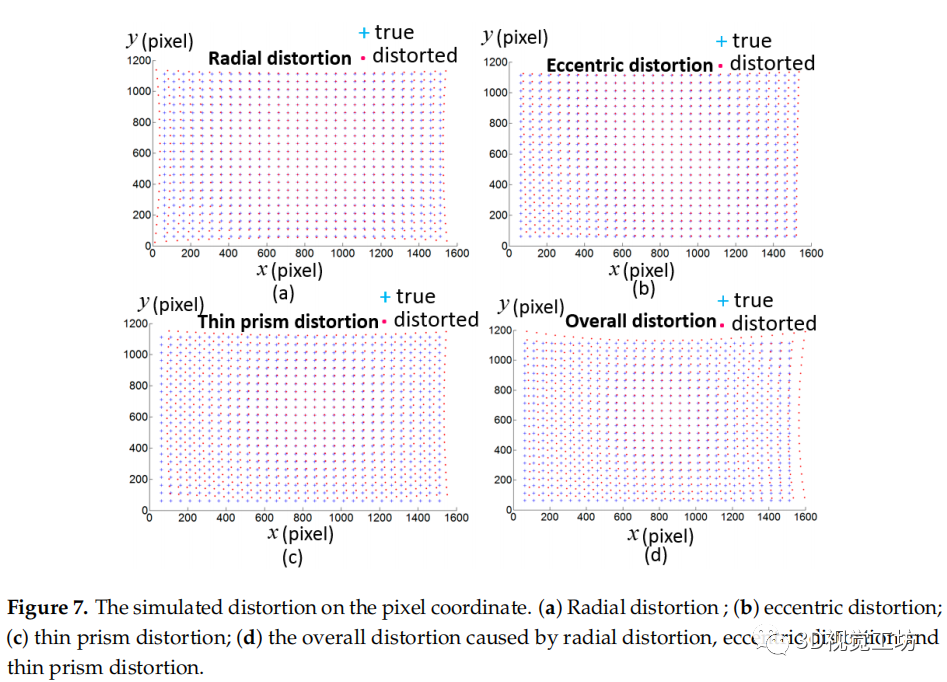
圖7 在像素坐標上的模擬畸變。（a） 徑向畸變 （b） 偏心畸變 （c） 薄棱鏡畸變 （d） 由徑向畸變、偏心畸變和薄棱鏡畸變引起的整體畸變。

其中： 是理想的像素。圖7顯示了模擬的理想像素和畸變像素。8個位姿的位姿被仿真，其中：

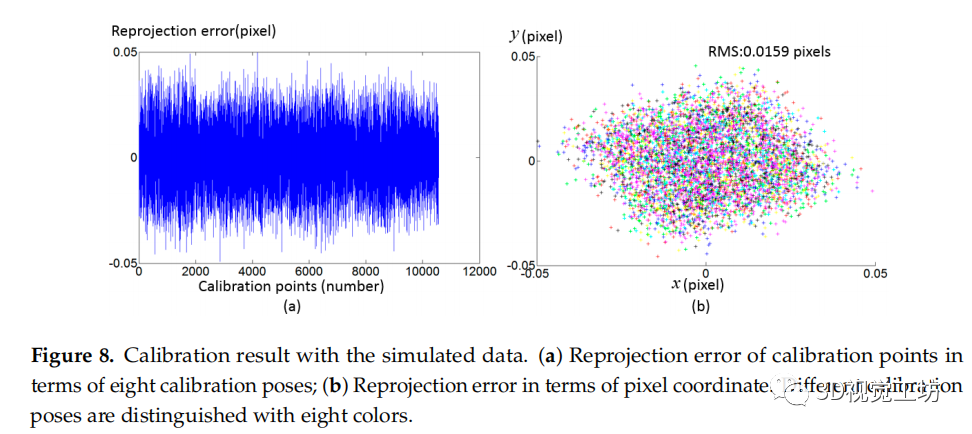
圖8 與模擬數據進行標定結果。（a）八個標定點的重投影誤差；（b）像素坐標的重投影誤差。不同的標定姿勢用八種顏色來區分。

在相位標靶中加入從0到0.005弧度的隨機噪聲。圖8顯示了所提出的標定方法的重投影誤差。結果表明，該標定方法能有效地補償復雜畸變源產生的相機畸變。

3.2 實驗研究

圖9 實驗設置

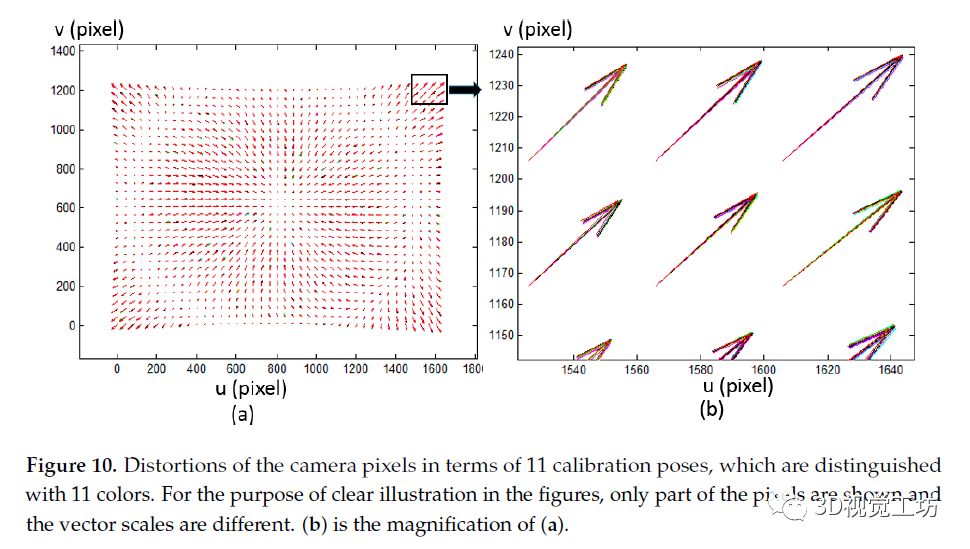
圖 10. 以 11 種顏色區分的 11 種標定姿勢下的相機像素畸變。為了在圖中清楚說明，僅顯示了部分像素并且矢量比例不同。（b） 是（a）放大倍數

為了驗證提出的方法，基于Lumenera CCD相機（Model Lw235M）進行了標定實驗。相機傳感器的分辨率是 ，相機鏡頭是一個35毫米固定焦距的原始鏡頭。一個CCD相機（戴爾E151 Fpp，分辨率為 ，飛利浦，上海，中國）用于相位靶標。一個CCD像素塊的大小為0.297mm。靶標被放置在11種不同的姿勢上。采用八步相移算法和頻率優化算法得到了絕對相位圖［19，20］，然后使用 的擬合窗口對相位圖進行平滑、插值。每10個相機像素被選擇形成一個大小為161×121的網格作為輸入，用世界坐標中的對應點標定相機。線性投影模型下所選像素的畸變如圖10所示。

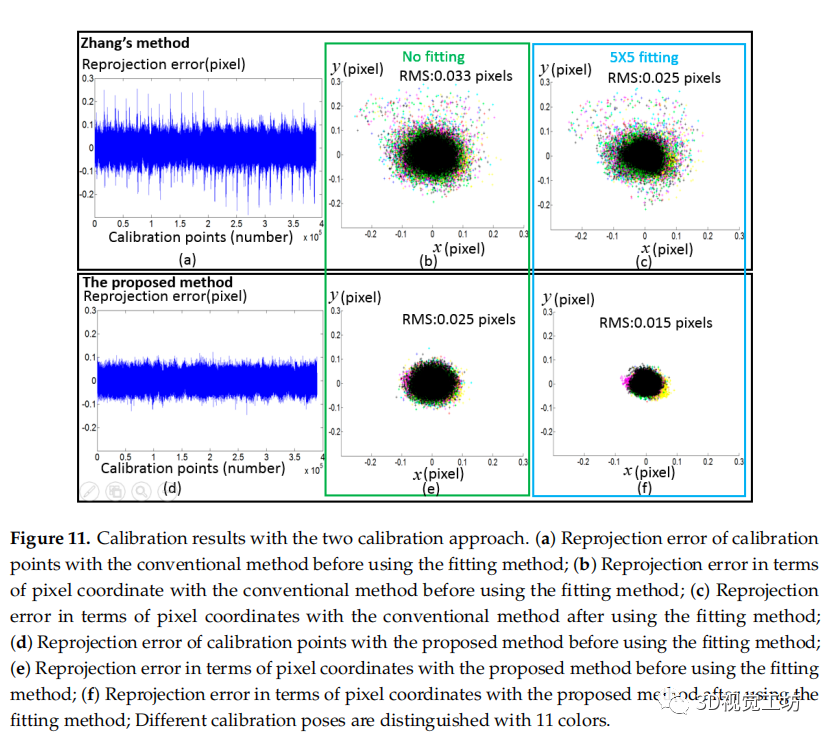
圖11 標定結果采用兩種標定方式。

（a） 使用擬合方法前用常規方法標定點的重投影誤差；

（b） 在使用擬合方法之前，用常規方法在像素坐標方面的重投影誤差；

（c） 使用擬合方法后與常規方法在像素坐標方面的重投影誤差；

（d） 在使用擬合方法之前，使用所提出方法的標定點的重投影誤差；

（e） 在使用擬合方法之前，用所提出的方法在像素坐標方面的重投影誤差；

（f） 使用擬合方法后所提出的方法在像素坐標方面的重投影誤差；不同的標定姿勢用 11 種顏色區分。

由于張正友標定法［1］和相應的工具箱在實際應用中非常普遍，因此我們的方法與張正友方法對比在圖11所示。張的方法可以分為四個步驟：（1）發現特征點和相機像素之間的對應位置；（2） 根據針孔模型計算相機參數和外參數的初始值；（3） 考慮基于數學模型的畸變補償；（4）利用Levenberg-Marquardt算法優化相機初始參數、外參數和畸變參數。可以從張的文章 ［1］ 中使用的棋盤或其他標定靶標中檢測到特征點。為避免不同標定靶標提取精度的差異，采用相同的相機像素和對應的物理點對兩種方法進行測試。使用所提出的方法，重投影誤差的 RMS 在應用擬合方法之前為 0.025 像素，在應用擬合方法之后為 0.015 像素。相比之下，傳統方法的重投影誤差的 RMS 在應用擬合方法之前為 0.033 像素，在應用擬合方法之后為 0.025 像素，分別比所提出的方法差 1.3 倍和 1.6 倍。

提出了一種基于全場相機像素和密集相位靶標的迭代畸變補償算法的相機標定方法。為了提高相位值的定位精度，研究了散焦、擬合和插值技術。在不依賴畸變數學模型的情況下，所提出的標定方法可以獲得逐像素的畸變和較高的標定精度。下一步將包括在偏轉測量系統中應用的建議標定方法。

如果將所提出的方法與其他基于非參數的畸變補償方法進行比較，那將是更可取的。然而，在這個實驗中有幾個不同的因素需要考慮：（1）很難獲得這些方法的開放代碼；（2） 其中一些方法基于特定的標定靶標，因此無法保證對比實驗具有相同的標定輸入。事實上，本文的仿真研究可以證明該方法的優越性，因為其他非基于參數的方法無法處理偏心畸變和薄棱鏡畸變，或者無法獲得內部參數相機 ［18］。該仿真研究表明，所提出的方法可以有效地標定具有復雜畸變條件的相機。基于這一點，可以得出結論，該方法優于其他基于非參數的畸變補償方法。

審核編輯：郭婷