目的
使用簡(jiǎn)單的“純跟蹤算法”實(shí)現(xiàn)無(wú)人車自動(dòng)泊車或者位姿調(diào)整。在泊車或者工業(yè)場(chǎng)景,如果空間不夠,那么車輛經(jīng)常需要做一些大角度的轉(zhuǎn)向或者倒車,例如叉車。
這些場(chǎng)景與一般的道路行駛場(chǎng)景可能有所區(qū)別,道路行駛一般只考慮前進(jìn)方向的高速行駛,并且轉(zhuǎn)向曲率不會(huì)太大。泊車場(chǎng)景恰好相反,曲率大、速度慢,而且伴隨行駛方向的變化。
道路行駛下的跟蹤已經(jīng)被研究的比較深入了,那么道路行駛使用的跟蹤算法還適用于倒車場(chǎng)景嗎?本文我們來(lái)研究一下這個(gè)問(wèn)題。

Reeds-Sheep曲線
假設(shè)無(wú)人車的運(yùn)動(dòng)路徑是已知的,筆者使用 https://github.com/hbanzhaf/steering_functions 中提出的曲率連續(xù)的改進(jìn)Reeds-Sheep曲線生成路徑。
程序輸出的路徑是一系列離散的點(diǎn),點(diǎn)之間的距離可以自定義,筆者選擇每5毫米一個(gè)點(diǎn),程序中設(shè)置DISCRETIZATION=0.005。
路徑采用nav_msgs::Path消息發(fā)出。
純跟蹤算法
純跟蹤算法(Pure Pursuit)首先要指定一個(gè)被跟蹤的目標(biāo)點(diǎn)。
原始版本的純跟蹤算法只討論了跟蹤無(wú)人車前方的點(diǎn),對(duì)于Reeds-Sheep曲線這種包含運(yùn)動(dòng)方向變化的曲線,無(wú)人車既需要前進(jìn)也需要后退,但是想實(shí)現(xiàn)后退也非常簡(jiǎn)單。
筆者將被跟蹤的目標(biāo)點(diǎn)稱為局部目標(biāo)(local goal)無(wú)人車真正最終的靜態(tài)目標(biāo)點(diǎn)則稱為全局目標(biāo)(global goal)。
純跟蹤需要無(wú)人車的定位,仿真時(shí)假設(shè)這個(gè)定位信息由ROS中的/base_pose_ground_truth消息給出。局部目標(biāo)的計(jì)算方式是,遍歷路徑,找到第一個(gè)離無(wú)人車≥ d l 的路徑點(diǎn)。
d l 就是前視距離,d l 越小跟蹤精度越高,但是越容易導(dǎo)致震蕩。機(jī)器人在運(yùn)動(dòng)時(shí),這個(gè)局部目標(biāo)也會(huì)更新。
如果找到的局部目標(biāo)落在了無(wú)人車的后方,此時(shí)意味著無(wú)人車需要后退,只需要將速度取負(fù)值即可,前輪轉(zhuǎn)角不用變。
出現(xiàn)的問(wèn)題
1.轉(zhuǎn)折點(diǎn)
在仿真時(shí)出現(xiàn)了一些問(wèn)題。首先,最困難的是對(duì)于尖點(diǎn)(cusp)怎么處理。因?yàn)楹芏嗲闆r下,Reeds-Sheep曲線都包含尖點(diǎn),在尖點(diǎn)處車輛會(huì)改變運(yùn)動(dòng)方向。
如果使用純跟蹤算法跟蹤這個(gè)路徑,那么在尖點(diǎn)處會(huì)出現(xiàn)一個(gè)問(wèn)題。因?yàn)榧兏櫵惴傄付ㄒ粋€(gè)跟蹤點(diǎn),這個(gè)跟蹤點(diǎn)一般在車輛前方或者后方一定距離(d l )處。
在向尖點(diǎn)運(yùn)動(dòng)時(shí),車輛不會(huì)正好處于尖點(diǎn)上,而是提前離開(kāi)。下圖中的d l = 0.2后面也采用這一數(shù)值。
圖中的黃點(diǎn)是被跟蹤的局部目標(biāo),紅色點(diǎn)表示無(wú)人車后輪軸中心處的實(shí)時(shí)位置。

這就導(dǎo)致車輛沒(méi)有完全位于路徑上,進(jìn)而導(dǎo)致后面的跟蹤出現(xiàn)橫向偏差(如下圖所示),即使采用曲率連續(xù)的Reeds-Sheep曲線版本也沒(méi)有用。

這是純跟蹤算法本身的問(wèn)題嗎?不是,純跟蹤算法完全可以跟得上,我們?yōu)榱税踩ǔ0演敵鼋嵌冉o限幅了,如果解除限幅你就會(huì)發(fā)現(xiàn)純跟蹤算法完全可以準(zhǔn)確的跟蹤。
但是實(shí)際使用時(shí)我們又不可能解除限幅,所以怎么解決這個(gè)問(wèn)題呢?
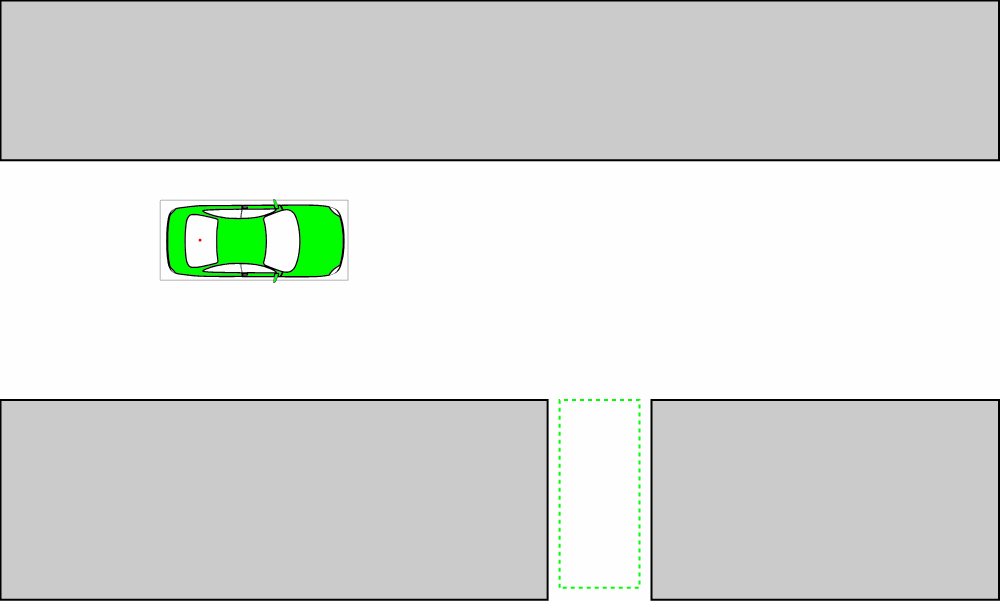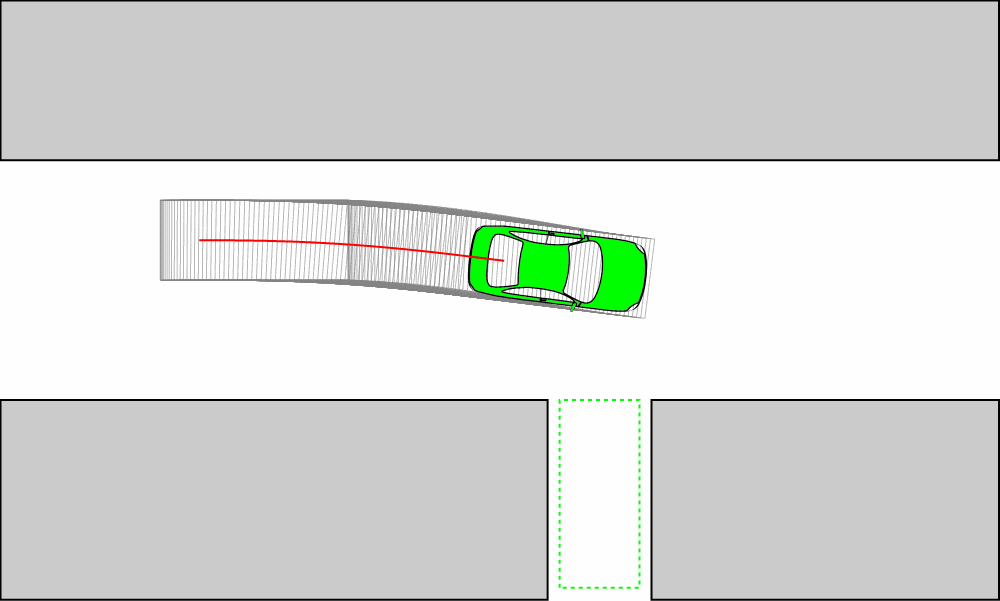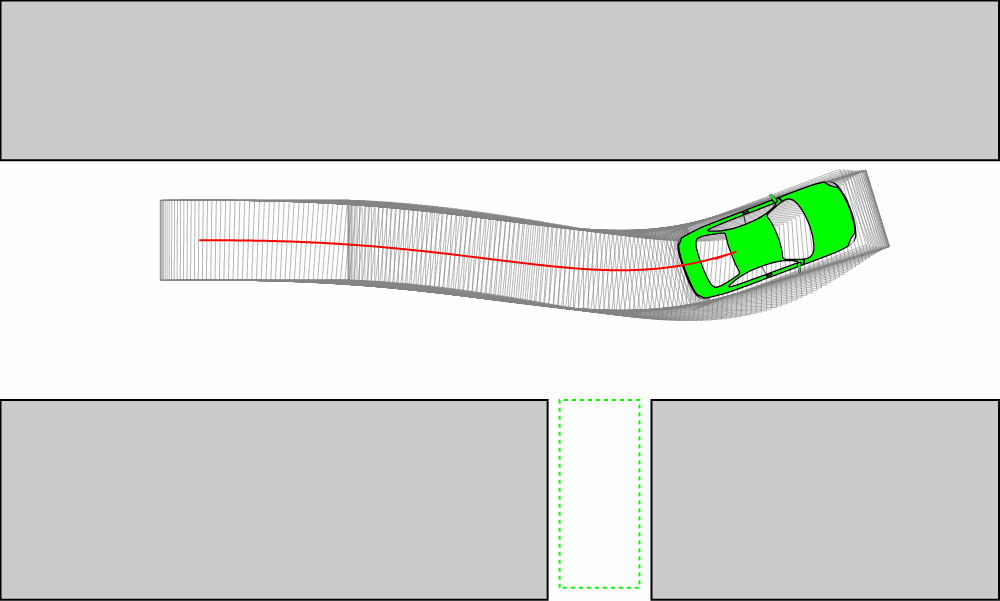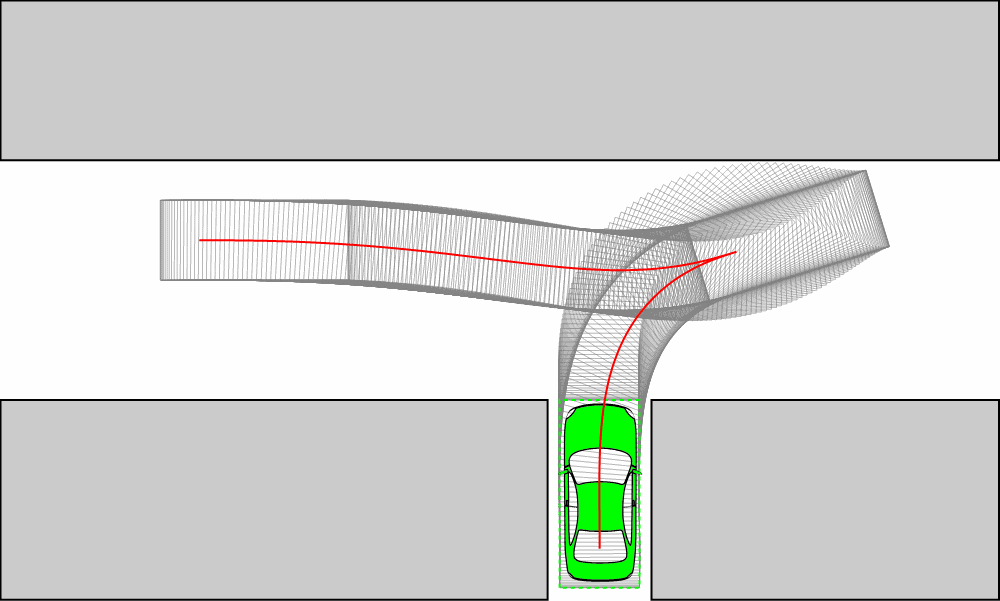
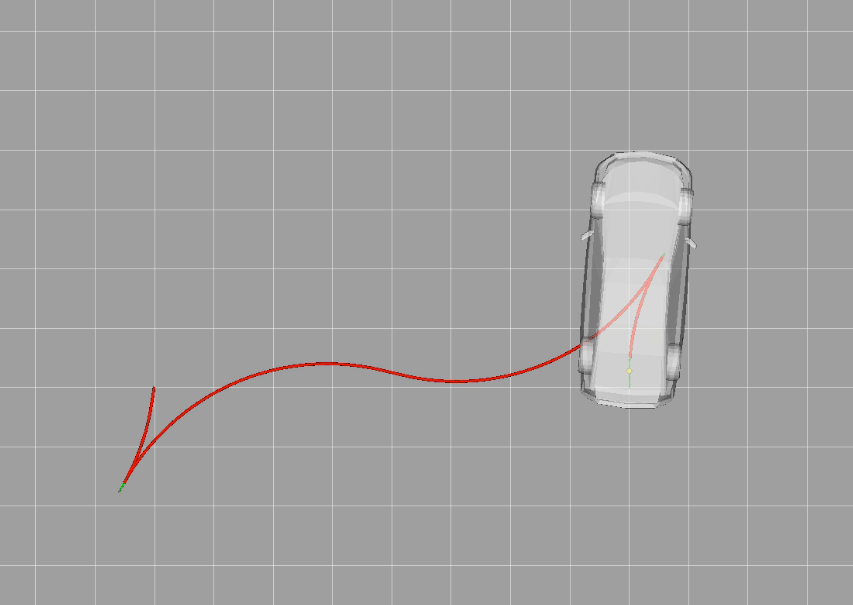
一種是直接增大一點(diǎn)Reeds-Sheep曲線的最小轉(zhuǎn)向半徑,令其略大于車輛的真實(shí)最小轉(zhuǎn)向半徑,筆者嘗試增加了約10%,跟蹤情況如下圖。
另一種方法是增加尖點(diǎn)(cusp)部分的長(zhǎng)度,這可以通過(guò)改變主程序(steering_functions_node.cpp)中的sigma_max_變量實(shí)現(xiàn),sigma_max_越小,過(guò)渡部分越長(zhǎng),最好大于d l 試驗(yàn)發(fā)現(xiàn)取sigma_max_=0.5左右就可以。
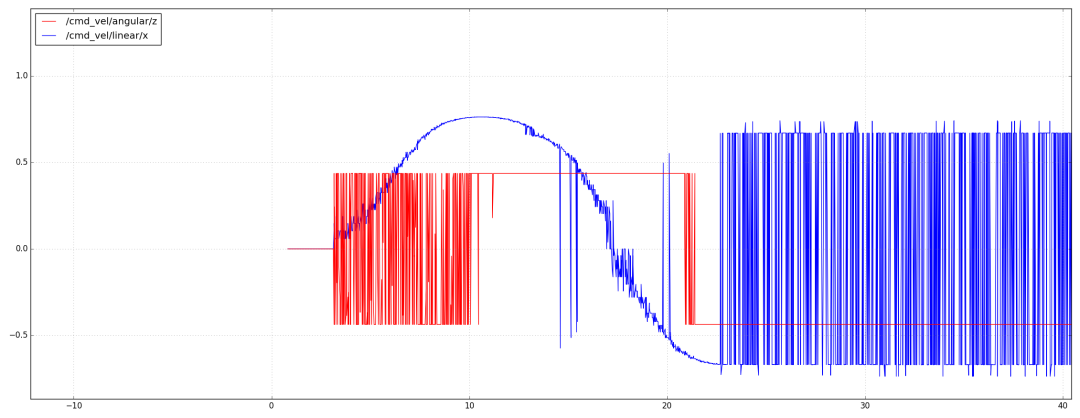
控制指令如下圖所示。
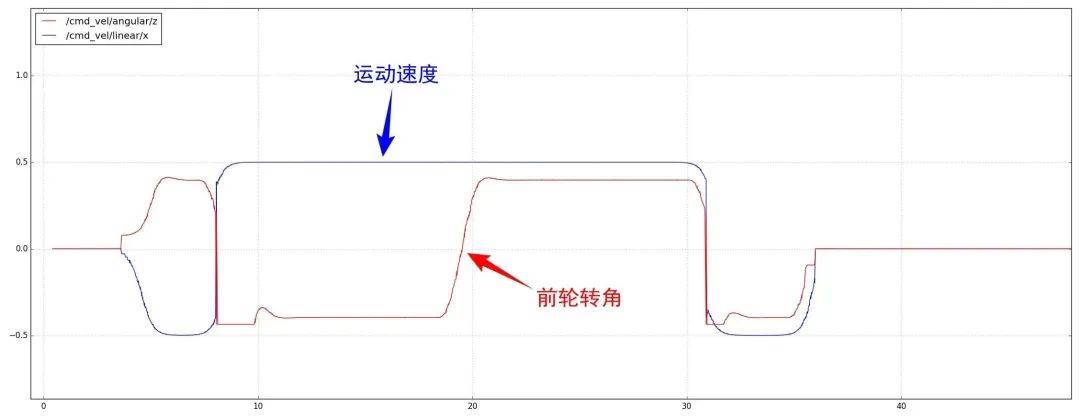
速度單獨(dú)進(jìn)行規(guī)劃,然后疊加到路徑上,如下圖所示。


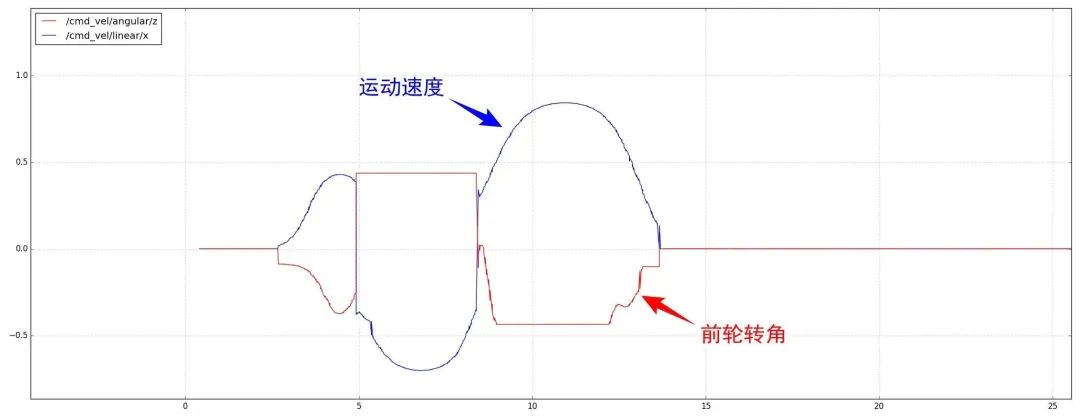
2.定位誤差
前面的控制都假設(shè)定位是完美的,不存在定位誤差。如果加入定位誤差,純跟蹤算法的表現(xiàn)會(huì)怎么樣呢?
我們用隨機(jī)數(shù)來(lái)模擬定位誤差,定位誤差一般是正太分布的,因此用正態(tài)分布函數(shù)std::normal_distribution生成隨機(jī)數(shù),均值總是取0,標(biāo)準(zhǔn)差決定了誤差的范圍。
首先取小的標(biāo)準(zhǔn)差—— 1mm,無(wú)人車的表現(xiàn)如下圖所示,無(wú)人車的跟蹤效果比較好。
但是前輪轉(zhuǎn)角的變化卻非常劇烈,如下圖所示。這還僅僅是1mm左右的誤差,這在實(shí)際中是幾乎不可能達(dá)到的。
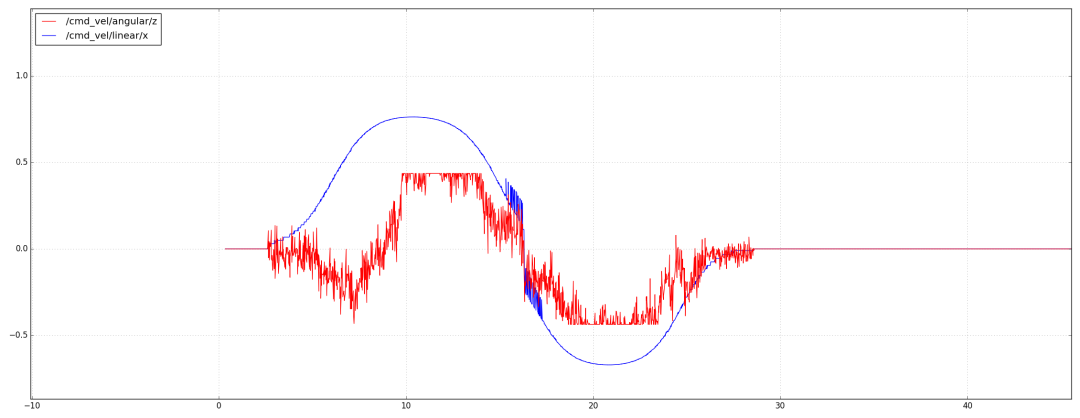
標(biāo)準(zhǔn)差為1cm時(shí)的表現(xiàn)如下圖所示,已經(jīng)產(chǎn)生了明顯的橫向跟蹤偏差。
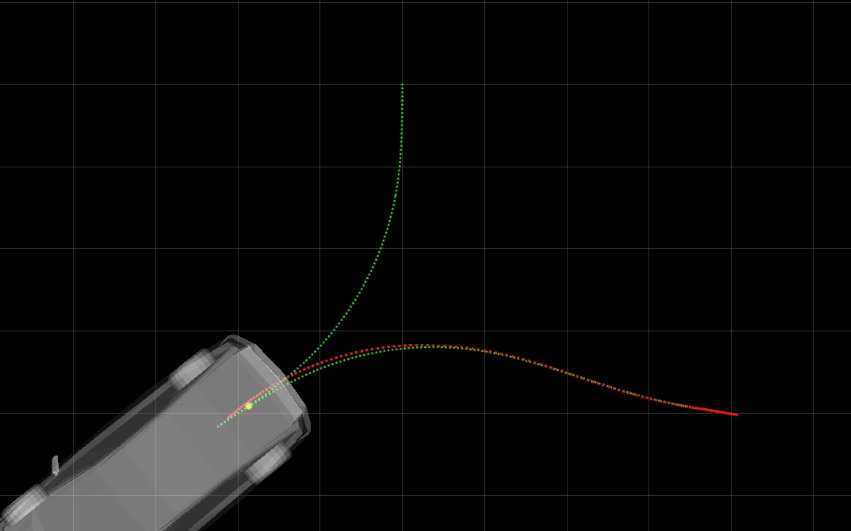
此時(shí)前輪轉(zhuǎn)角已經(jīng)慘不忍睹了,如下圖所示,這還是1cm左右的誤差,實(shí)際中無(wú)人車的定位要達(dá)到1cm也是很困難的。
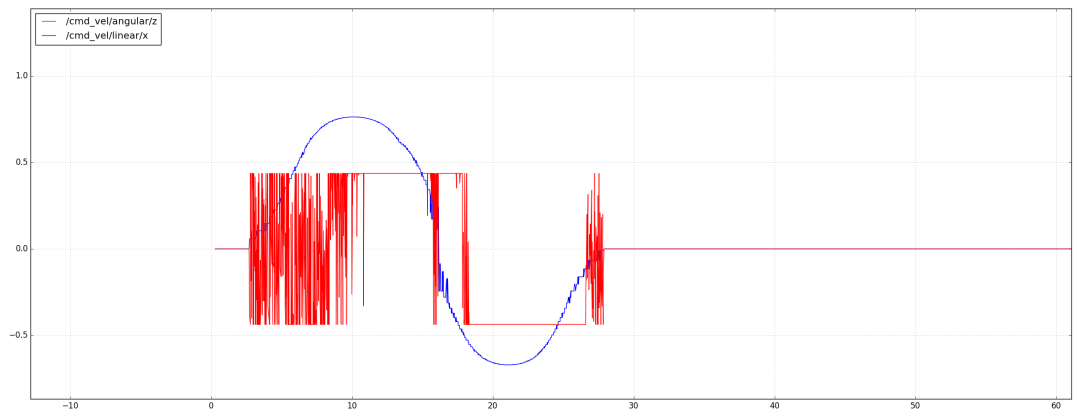
標(biāo)準(zhǔn)差為5cm時(shí)的表現(xiàn)如下圖所示,這個(gè)誤差是一般室外衛(wèi)星定位的誤差范圍,也就是常見(jiàn)的誤差,此時(shí)無(wú)人車徹底無(wú)法跟蹤。
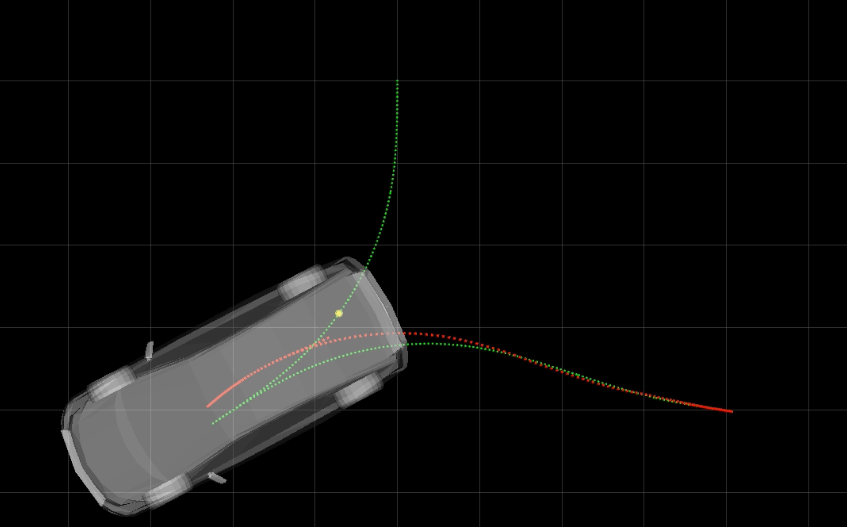
不僅前輪轉(zhuǎn)角更瘋狂了,而且由于橫向偏差已經(jīng)超過(guò)了前視距離d l ,局部目標(biāo)已經(jīng)出現(xiàn)在無(wú)人車側(cè)面了,導(dǎo)致無(wú)人車完全無(wú)法跟蹤了,如下圖所示。
這說(shuō)明純跟蹤算法對(duì)定位誤差是極其敏感的,在實(shí)際應(yīng)用時(shí)這是個(gè)非常嚴(yán)重的問(wèn)題。
算法理解
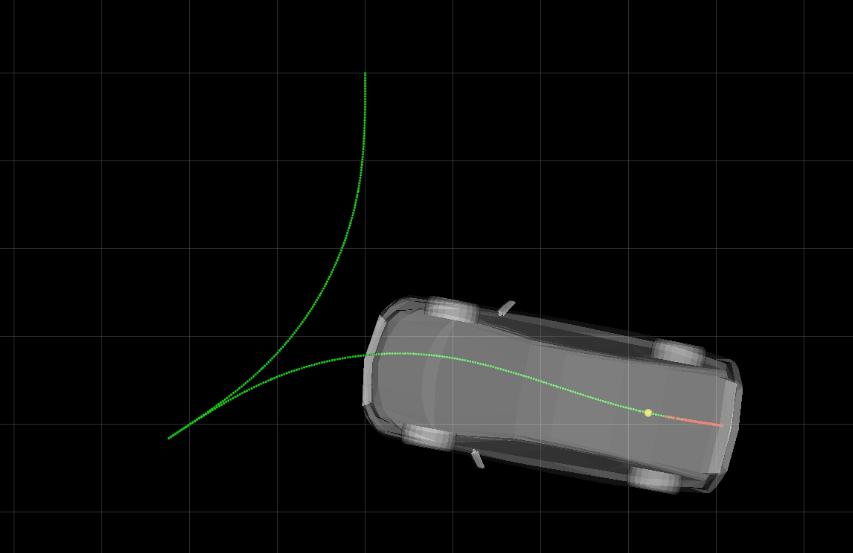
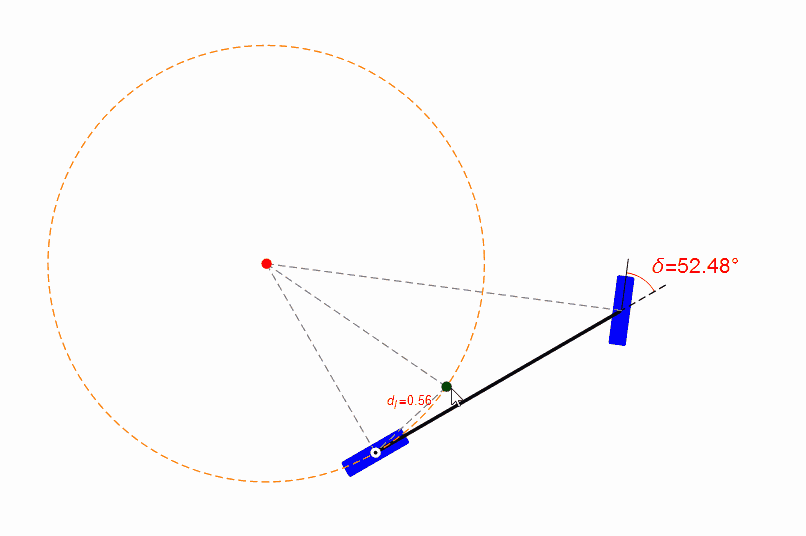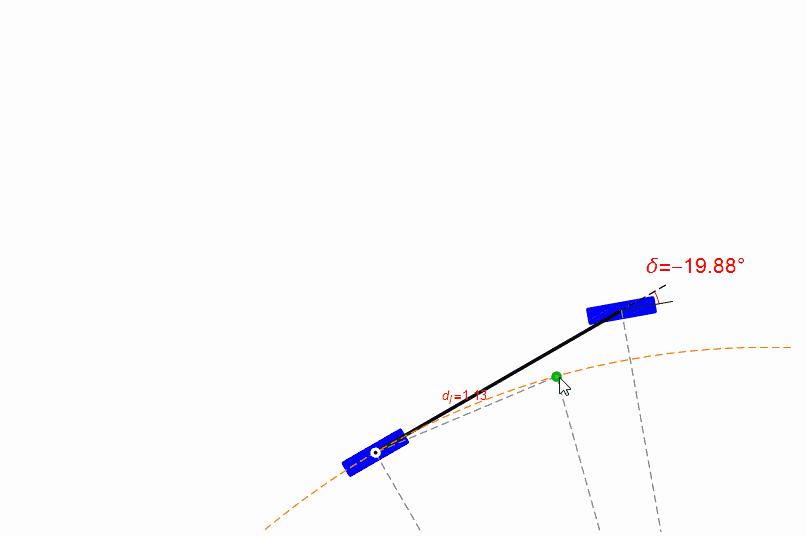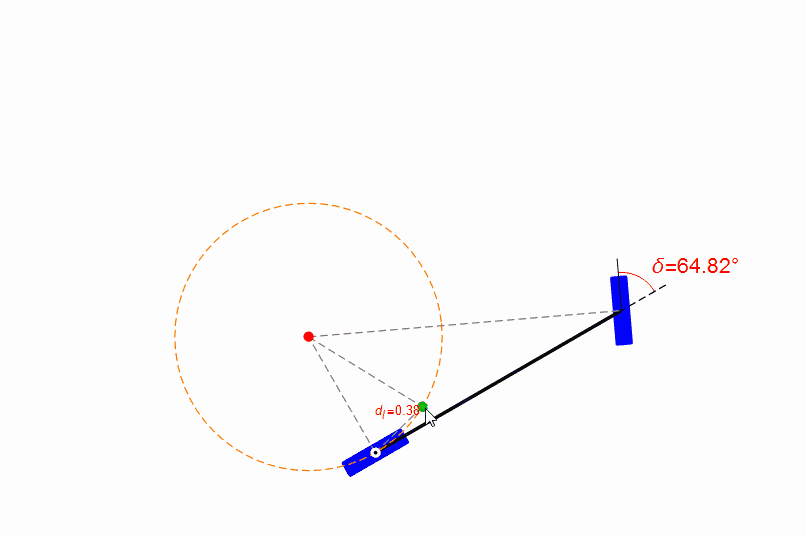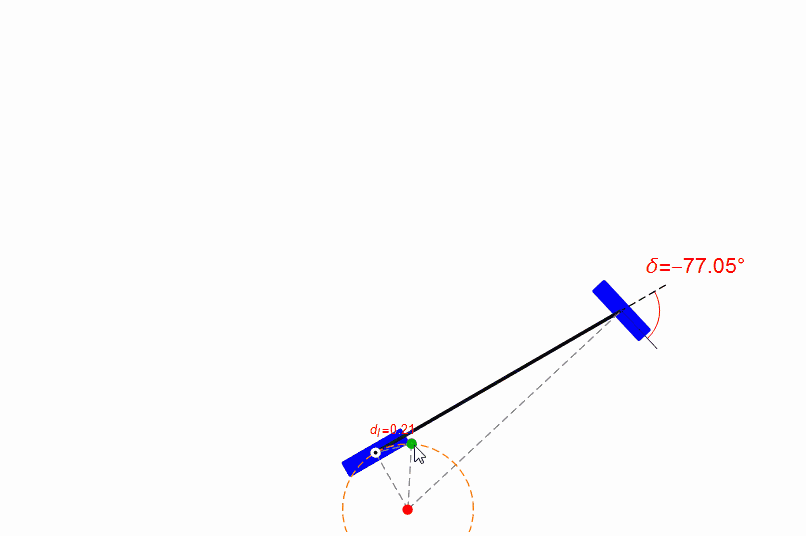
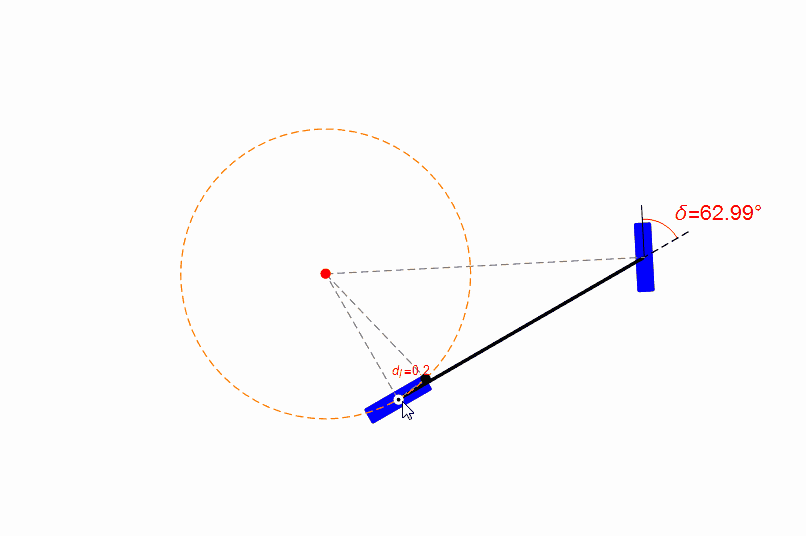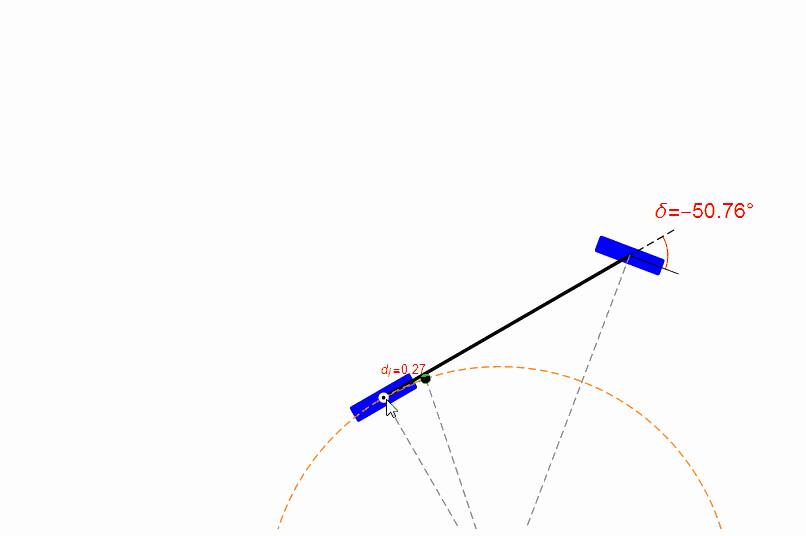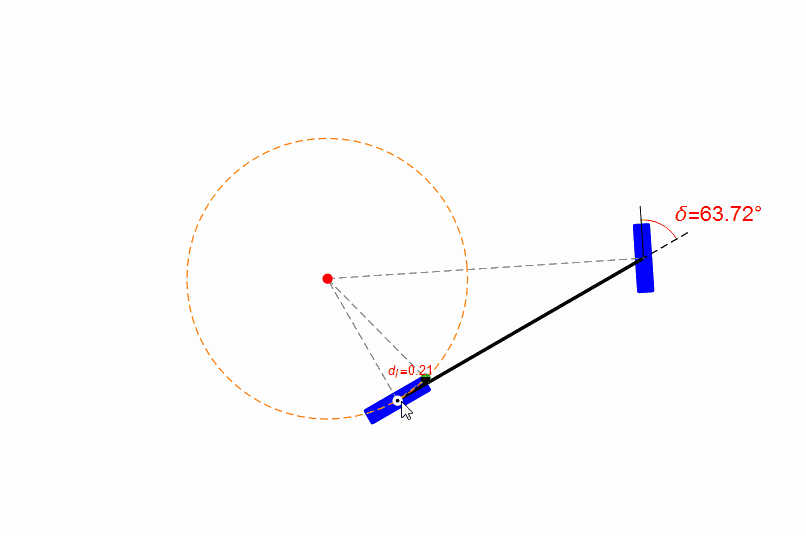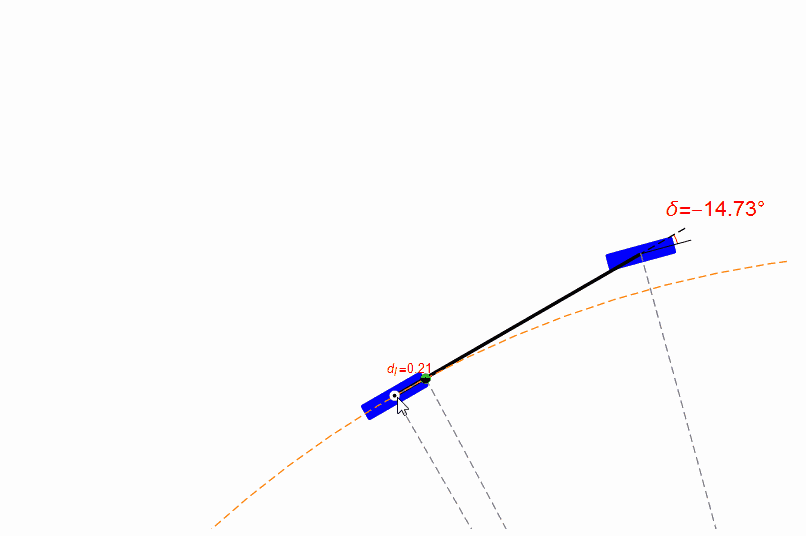
為了易于理解純跟蹤算法,筆者用Mathematica設(shè)計(jì)了一個(gè)小程序,你可以用鼠標(biāo)拖動(dòng)目標(biāo)點(diǎn)(綠色點(diǎn)),并觀察前輪的轉(zhuǎn)角,如下圖。
目標(biāo)點(diǎn)是純跟蹤算法中的核心概念,這個(gè)目標(biāo)點(diǎn)是人為設(shè)計(jì)或者選擇的。跟蹤性能的好壞不僅取決于控制參數(shù)的選擇,目標(biāo)點(diǎn)的選擇也起到重要的作用。
當(dāng)目標(biāo)點(diǎn)選取的不好時(shí),例如距離無(wú)人車當(dāng)前位置過(guò)近,則會(huì)出現(xiàn)控制量劇烈變化。
你也可以用鼠標(biāo)拖動(dòng)無(wú)人車的參考點(diǎn),觀察前輪的轉(zhuǎn)角,如下圖。從圖中可以發(fā)現(xiàn),在距離目標(biāo)比較近時(shí),純跟蹤算法的表現(xiàn)很糟糕,參考點(diǎn)位置有一點(diǎn)點(diǎn)改變都會(huì)導(dǎo)致前輪轉(zhuǎn)角劇烈變化。
但是無(wú)人車的定位本身是必然存在偏差的,所以純跟蹤算法在前視距離短時(shí)穩(wěn)定性并不好。
cuboid[center_: {0, 0}, dim_, radius_: 0] := Rectangle[center - dim/2, center + dim/2, RoundingRadius -> 0.01];
move2D[shape_, pose_] := Translate[Rotate[shape, pose[[3]], {0, 0}], pose[[1 ;; 2]]];
L = 1.64;
[Delta]max = 25 Degree ;
bicycle[pose_, [Delta]_] := {
rearWheel = cuboid[{0, 0}, {0.4, 0.1}, 0.1];
frontWheel = move2D[rearWheel, {L, 0, [Delta]}];
trunk = cuboid[{L/2, 0}, {L, 0.02}, 0.1];
move2D[{Blue, frontWheel, rearWheel, Black, trunk, Red, Circle[{L, 0}, 0.22, {0, [Delta]}]}, pose]
};
Manipulate[
pose = Flatten@{p, [Theta]};
dirvec = AngleVector[[Theta]];
vertvec = {-dirvec[[2]], dirvec[[1]]};
p1 = p + L*dirvec;
dl = Norm[goal - p];
[Alpha] = VectorAngle[goal - p, {1, 0}] - [Theta];
[Delta] = ArcTan[2*L*Sin[[Alpha]]/dl];
R = Abs[dl/2/Sin[[Alpha]]];
c = p + Sign[[Alpha]]*R*vertvec;
a1 = -VectorAngle[p - c, {1, 0}];
a2 = -VectorAngle[goal - c, {1, 0}];
Graphics[{bicycle[pose, [Delta]], Point[c], AbsoluteThickness[1],
Line[{p1, p1 + AngleVector[[Theta] + [Delta]]*0.3}], AbsoluteDashing[{6, 3}], Black, Line[{p, p1 + dirvec*0.3}], Gray, Line[{p, c}], Line[{c, goal}], Line[{goal, p}], Line[{c, p1}], Orange, Circle[c, R(*,{a1,a2}*)], AbsolutePointSize[8], White, Point[p], Red, Point[c], Darker@Green, Point[goal], Red, Text[Style[ "[Delta]=" <> ToString@Round[[Delta]*180/Pi, 0.01] <> "[Degree]", FontSize -> 16], p1 + dirvec*0.5], Text["!(*SubscriptBox[(d), (l)])=" <> ToString@Round[dl, 0.01], (p + goal)/2 + {0, 0.1}]},
ImageSize -> 600, PlotRange -> 1.5 {{-1.5, 1.5}, {-0.5, 1.5}},
Axes -> False], {{p, {0, 0}}, Locator, Appearance -> Graphics@Point[{0, 0}]}, {{goal, {0.16, 0.12}}, Locator, Appearance -> Graphics[{Green, Point[{0, 0}]}]}, {{[Theta], Pi/6}, 0, 2 Pi, 0.01}, TrackedSymbols :> True, Initialization :> {goal = {0.16, 0.12}}]
審核編輯 :李倩
-
跟蹤算法
+關(guān)注
關(guān)注
0文章
41瀏覽量
13024 -
自動(dòng)泊車
+關(guān)注
關(guān)注
0文章
104瀏覽量
13699 -
無(wú)人車
+關(guān)注
關(guān)注
1文章
303瀏覽量
36499
原文標(biāo)題:純跟蹤算法用于無(wú)人車自動(dòng)泊車
文章出處:【微信號(hào):vision263com,微信公眾號(hào):新機(jī)器視覺(jué)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
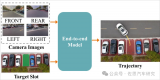
端到端在自動(dòng)泊車的應(yīng)用

智駕仿真測(cè)試實(shí)戰(zhàn)之自動(dòng)泊車HiL仿真測(cè)試

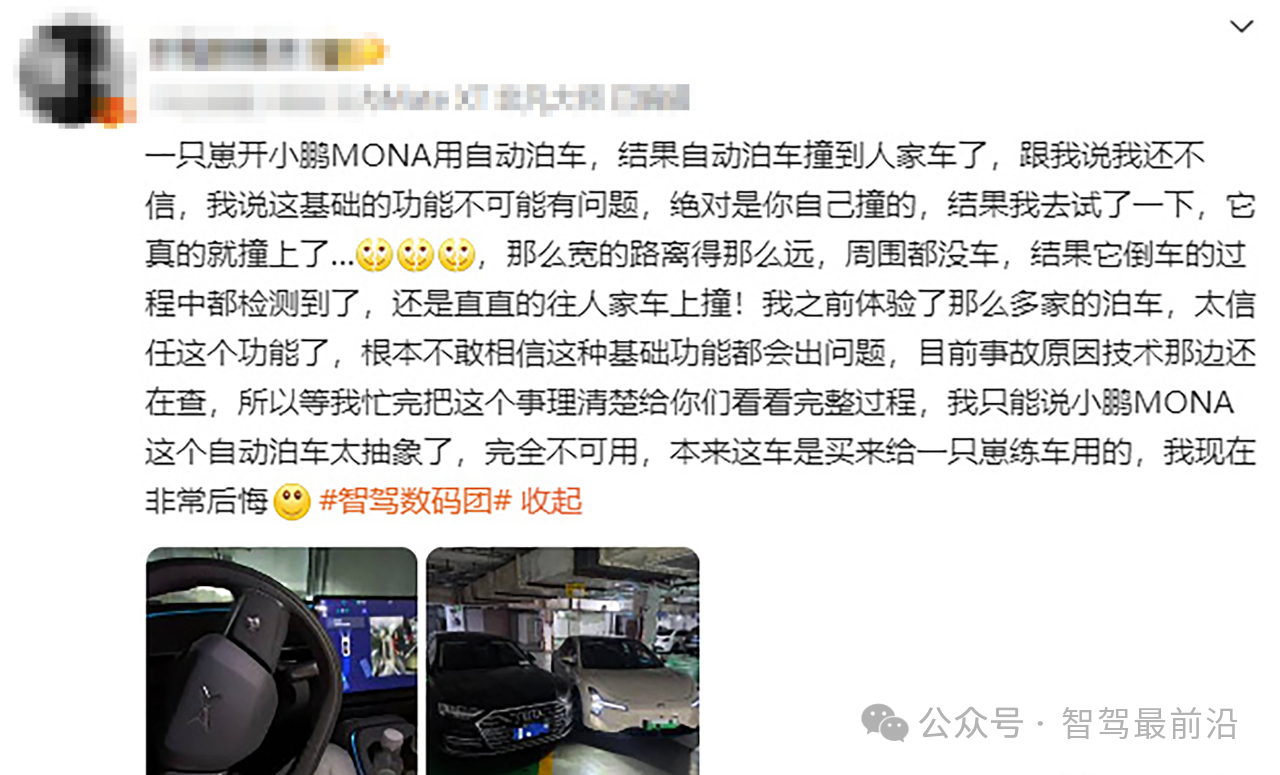
從小鵬M03自動(dòng)泊車撞上奧迪聊聊智駕現(xiàn)狀
自動(dòng)共振跟蹤的優(yōu)勢(shì)

抖動(dòng)跟蹤不丟失 慧視圖像跟蹤板和自研算法強(qiáng)勢(shì)升級(jí)

宏景智駕自動(dòng)泊車2.0系統(tǒng)征服高難度車位
FPGA在自動(dòng)駕駛領(lǐng)域有哪些應(yīng)用?
超聲波雷達(dá)在APA自動(dòng)泊車功能中的應(yīng)用與仿真

極氪007推送ZEEKR OS 6.1,實(shí)現(xiàn)量產(chǎn)機(jī)械車位自動(dòng)泊車?
智界S7將于六月全球首發(fā)自動(dòng)泊車與召喚VPD商用功能
極氪007公測(cè)啟動(dòng),量產(chǎn)機(jī)械車位自動(dòng)泊車業(yè)內(nèi)首創(chuàng)
特斯拉全新自動(dòng)泊車功能上線,可平行泊車
常用的焊縫自動(dòng)跟蹤傳感器有哪些





 純跟蹤算法用于無(wú)人車自動(dòng)泊車
純跟蹤算法用于無(wú)人車自動(dòng)泊車










評(píng)論