論文地址:https://arxiv.org/pdf/1904.07220v1.pdf
代碼:pytracking 中有 dimp 的代碼
摘要
與大多數其他視覺問題相比,跟蹤需要在推理階段在線學習魯棒的特定于目標的外觀模型。為了能夠進行端到端的培訓,目標模型的在線學習因此需要自身嵌入到跟蹤體系結構中。由于這些困難,流行的孿生網絡僅預測了目標特征模板。但是,這種模型由于無法集成背景信息而具有有限的判別能力。
我們開發了一種端到端的跟蹤體系結構,能夠充分利用目標和背景外觀信息來進行目標模型預測。通過設計專用的優化過程(僅需幾次迭代即可預測功能強大的模型),我們的體系結構源自有區別的學習損失。此外,我們的方法能夠學習判別損失本身的關鍵方面。我們的跟蹤器在6個跟蹤基準上設置了最新技術,在VOT2018上EAO得分0.440,運行40FPS。
1.簡介
目前孿生網絡學習框架仍受到嚴重限制。首先,孿生網絡跟蹤者僅在推斷模型時利用目標外觀。這完全忽略了背景外觀信息,這對于將目標與場景中的相似對象區分開來至關重要(請參見圖1)。其次,所學習的相似性度量對于未包含在離線訓練集中的對象不一定是可靠的,從而導致沒有泛化能力。第三,大部分孿生網絡不能更新模型,有更新的算法求助于簡單的模板平均(DA-SiamRPN,干擾物感知模型,到跟蹤幀時,模板z和當前位置 p_k 計算相似度之后,減去當前位置與檢測幀中其他位置的相似度的加權和,可以更新模型提高精度)。與其他最新跟蹤方法相比,這些局限性導致魯棒性較差。
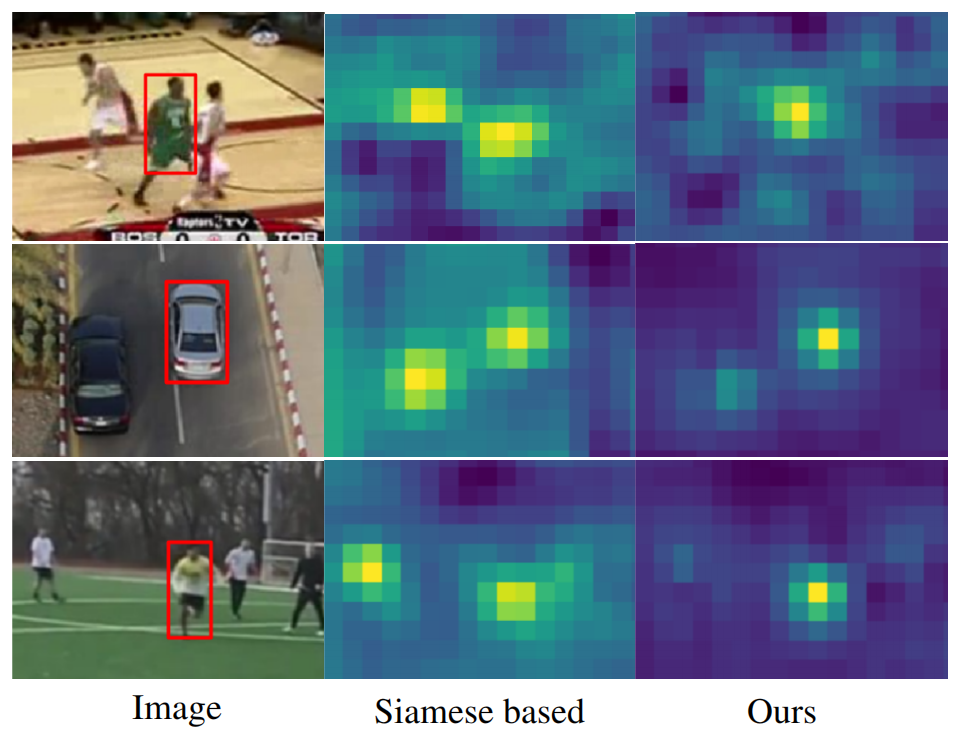
在這項工作中,我們引入了一種以端到端的方式訓練的替代跟蹤體系結構,該體系結構直接解決了所有上述限制。在我們的設計中,我們從判別性學習(Discriminative Learning Loss)過程中汲取了靈感。我們的方法基于目標模型預測網絡,該網絡是通過應用迭代優化過程從判別性學習損失中得出的。該體系結構可以進行有效的端到端訓練,同時最大程度地提高預測模型的判別力。通過確保通過兩個關鍵設計選擇最少的優化步驟來實現這一目標。
首先,我們采用基于最速下降法的方法來計算每次迭代的最佳步長。其次,我們集成了一個模塊,該模塊可以有效地初始化目標模型。此外,我們通過學習判別損失本身,將極大的靈活性引入了最終的架構。
我們的整個判別式跟蹤體系結構,以及主干特征提取器,都通過標注注釋的跟蹤序列來進行訓練,方法是將未來幀的預測誤差降至最低。
2.相關工作
RPN詳細介紹:https://mp.weixin.qq.com/s/VXgbJPVoZKjcaZjuNwgh-A
SiamFC詳細介紹:https://mp.weixin.qq.com/s/kS9osb2JBXbgb_WGU_3mcQ
SiamRPN詳細介紹:https://mp.weixin.qq.com/s/pmnip3LQtQIIm_9Po2SndA
SiamRPN++詳細介紹:https://mp.weixin.qq.com/s/a9wt67Gn5JowQ4eOmgX75g
孿生網絡方法的一個關鍵限制是它們無法將背景區域或先前跟蹤的幀中的信息合并到模型預測中。
3.方法
與在孿生網絡跟蹤器中一樣,我們的方法得益于端到端培訓。但是,與Siamese不同,我們的體系結構可以充分利用背景信息,并提供有效的手段來用新數據更新目標模型。
我們的模型預測網絡來自兩個主要原理:(1)一個判別力強的損失函數可以指導網絡學到魯棒的特征;(2)一個powerful的優化器可以加快網絡收斂。
我們的架構僅需幾次迭代即可預測目標模型,而不會損害其判別能力。在我們的框架中,目標模型構成卷積層的權重,提供目標分類分數作為輸出。
我們的模型預測體系結構通過將一組帶 bb 注釋的圖像樣本作為輸入來計算這些權重。模型預測器包括一個初始化程序網絡,該初始化程序網絡僅使用目標外觀即可有效提供模型權重的初始估計。然后由優化器模塊處理這些權重,同時考慮目標樣本和背景樣本。通過設計,我們的優化器模塊幾乎沒有需要學習的參數,以避免在離線訓練期間過分適應某些類別和場景。因此,我們的模型預測變量可以泛化到其他的對象,這在通用對象跟蹤中至關重要。
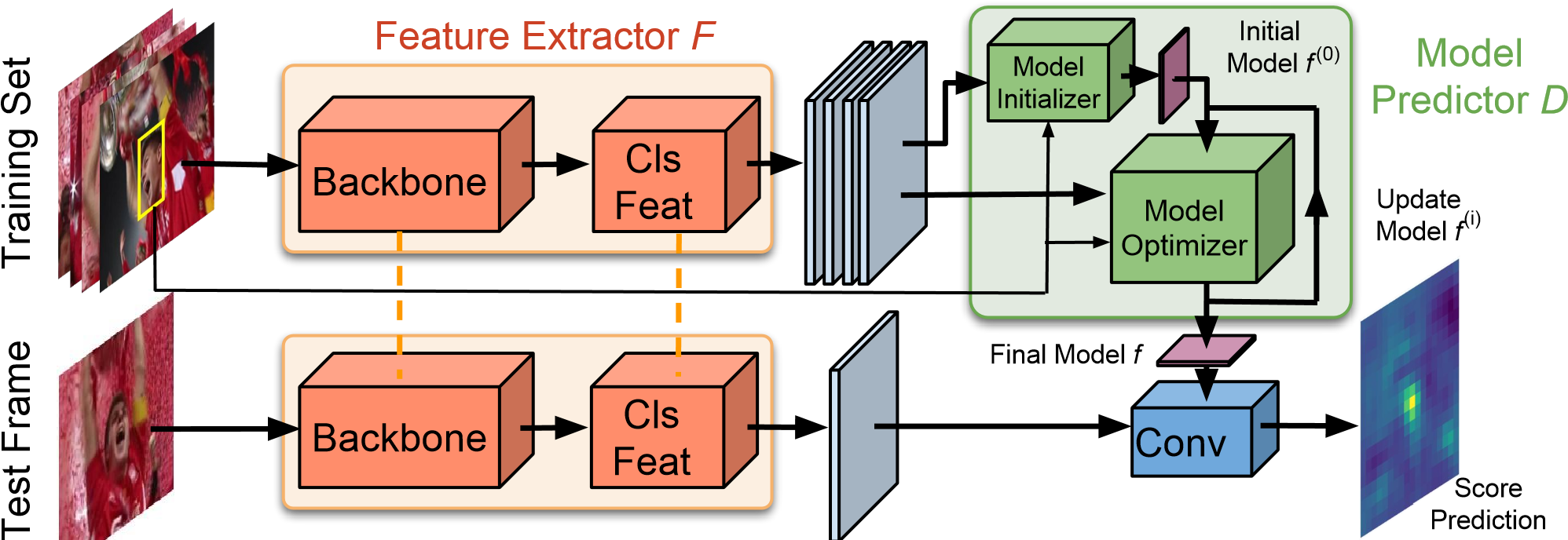
圖2.我們的跟蹤架構概述。給定帶注釋的訓練集(左上),我們使用骨干網絡提取深度特征圖,然后再附加卷積塊(Cls Feat)。然后將特征圖輸入到由初始化器(initializer)和循環優化器模塊(optimizer)組成的模型預測器D。模型預測器輸出卷積層的權重,該卷積層對從測試幀中提取的特征圖執行目標分類。為了清楚起見,此處未顯示邊界框回歸分支。
我們的最終跟蹤架構如圖2所示。我們的網絡包括兩個分支:分類和回歸。兩個分支都從通用骨干網輸入深層功能。
目標分類分支包含一個卷積塊,提取出分類器對其進行操作的特征。給定一組訓練樣本和相應的目標框,模型預測器將生成目標分類器的權重。然后將這些權重應用于從測試幀中提取的特征,以計算目標置信度分數。
對于bb框估計分支,我們利用基于重疊最大化(就是在目標檢測網絡上增加了一個IoU分支,用于預測bb與gt的IoU,使用最大化IoU來調整bb)的體系結構。它可以預測目標和一組proposal boxes之間的IoU。
整個跟蹤網絡,包括目標分類,bb估計和骨干模塊,都在跟蹤數據集中進行了離線培訓。
3.1 Discriminative Learning Loss
判別性學習損失
論文提出了一個概念,就是單純以圖片對方式訓練,傳統的方法只會讓網絡過分注意于優化負樣本的影響,而忽略了學到的正樣本的特征本身的判別能力。為了解決這個問題,他們用了SVM中使用的hinge-like損失,就是不僅將前景背景分開,更加使得兩類之間有一定的距離,使得分類結果更好。
在本節中,我們描述用于推導模型預測體系結構的判別性學習損失。我們的模型預測器 D 的輸入由特征提取器網絡 F 生成的深度特征圖 x_j \\in X 訓練集 S_{train}=(x_j,c_j)^n_{j-1} 組成。每個樣本與相應的目標中心坐標 c_j \\in R^2 對。有了這些數據,我們的目標是預測目標模型 f=D(S_{train}) 。模型 f=D(S_{train}) 定義為卷積層的濾波器權重,該卷積層的特征是區分特征空間 x 中的目標外觀和背景外觀。
L(f)= \\frac{1}{|S_{train}|} \\sum_{(x,c) \\in S_{train}} ||r(x*f,c)||^2+||\\lambda f||^2\\tag{1}
在這里,*表示卷積,\\lambda為正則化因子。函數 r(s,c) 根據目標置信度得分 s=x*f 和 gt 中心坐標 c 計算每個空間位置的殘差。最常見的選擇是 r(s,c)=s-y_c ,其中 y_c 是每個位置的期望目標分數,通常設置為以 c 為中心的高斯函數。然而,簡單地求差通常會使模型對所有負樣本回歸校準的置信度得分為零,這需要學習將重點放在負面數據樣本上,而不是獲得最佳的判別能力。簡單的差異并不能解決目標與背景之間數據不平衡的問題。
為了解決數據不平衡的問題,我們使用空間權重函數 v_c。下標 c 表示目標的中心位置的依賴性,如3.4節所述。為了適應第一個問題,我們按照支持向量機的原理修改了損失。我們采用hinge-like loss,用 max(0,s) 將背景區域中的負分數取零。因此,該模型可以自由地為背景中的簡單樣本預測較大的負值,而不會增加損失。另一方面,對于目標區域,我們發現添加類似的hinge-like loss max(0,1-s) 是不利的,因為目標類和背景類之間的基本不對稱,數值上不平衡。此外,在跟蹤情況下,例如精確校準的目標置信度確實是有利的。
為了兼顧最小二乘回歸和hinge loss的優點,我們定義了殘差函數:
r(s,c)=v_c *(m_cs+(1-m_c)max(0,s)-y_c)\\tag{2}
目標區域mask由 m_c 定義,其值在每個空間位置 t \\in R^2 有 m_c(t) \\in[0,1],即正樣本就用正樣本的score,負樣本的話就用大于零的。同樣,下標c表示對目標中心坐標的依賴性。上式能夠根據相對于目標中心c的圖像位置連續地將損失從標準最小二乘回歸更改為hinge loss。將 m_c \\approx 1 設置為目標,將 m_c \\approx 0 設置為背景會產生上述所需的行為。但是,如何最佳設置 m_c 尚不清楚,特別是在目標和背景之間的過渡區域。盡管經典策略是使用試錯法手動設置 mask 參數,但我們的端到端公式允許我們以數據驅動的方式學習 mask。實際上我們的方法都是網絡中自己學到的,并不是人工指定的:目標 mask m_c,空間權重 v_c ,正則化因子 \\lambda。
3.2 Optimization-Based Architecture
基于優化的架構
作者表示使用固定的學習率不僅會導致模型迭代次數多,獲得的精度也不夠理想,所以作者自己設計了一個梯度下降的方式,自適應的學到學習率。這里的策略就是希望梯度下降沿著最陡的方向走。
我們得出網絡架構D,它通過公式(1)最小化誤差來預測濾波器f=D(S_{train})。該網絡是通過制定優化程序來設計的。從等式(1)和(2)我們可以得出損耗 \\nabla L 相對于濾波器 f 的梯度的表達式。直接的選擇是使用步長來梯度下降。
f^{i+1}=f^i-\\alpha \\nabla L(f^i) \\tag{3}
梯度下降的緩慢收斂主要是由于步長不變,所以步長不依賴于數據或當前模型估計。我們通過推導使用了更復雜的優化方法來解決此問題,該方法僅需要進行幾次迭代即可預測出強大的判別濾波器 f。核心思想是基于最速下降法計算步長,這是一種常見的優化技術。我們首先在當前估計值 f^i 處用二次函數來估算損失:
L(f)\\approx \\tilde{L}(f)=\\frac 1 2 (f-f^i)^TQ^i(f-f^i)+(f-f^i)T\\nabla L(f^i)+L(f^i) \\tag{4}
在這里,濾波器變量 f 和 f_i 被視為向量,而 Q^i 是正定方陣。然后,通過找到使梯度方向上的近似損失最小的步長來進行最陡的下降:
\\alpha=\\frac{\\nabla L(f^i)^T \\nabla L(f^i)^T}{\\nabla L(f^i)^TQ^i \\nabla L(f^i)} \\tag{5}
在最速下降時,公式(5)用于計算濾波器更新的每次迭代中的標量步長。
二次模型(4)以及因此得到的步長(5)取決于 Q^i 的選擇。例如,通過使用縮放的單位矩陣 ,我們以固定步長來重新獲取標準梯度下降算法。對于我們的最小二乘公式(1),Gauss-Newton方法提供了一個強大的替代方法,因為它僅涉及一階導數,因此具有明顯的計算優勢。因此,我們設置 Q^i=(j^i)^T J^i,其中 J^i 是 f^i 處殘差的雅可比行列式。實際上,矩陣 Q^I 和 J^i 都不需要顯式構造,而是實現為一系列神經網絡操作。
3.3 Initial filter prediction
初始過濾器預測
這個模型初始化就是將所有的 bbox 里面的東西取平均,就像原始的 Siamese 網絡一樣,只不過在這里只用于初始化,后面還會訓練更新。
為了進一步減少預測模塊D中所需的優化遞歸次數,我們引入了一個經過訓練的小型網絡模塊以預測初始模型評估 f^0 。我們的初始化器網絡由一個卷積層和一個精確的 ROI 池化層組成。ROI 池化層從目標區域中提取特征并將其合并為與目標模型 f 相同的大小。然后將合并的特征圖對 s_{train} 中的所有樣本求平均值,以獲得初始模型 f^0 。與孿生網絡跟蹤器一樣,此方法僅利用目標特征。但是,我們的初始化程序網絡僅負責提供初始估計值,而不是預測最終模型,然后由優化程序模塊進行處理以提供最終的判別模型。
3.4 Learning the Discriminative Loss
學習判別性損失
這個部分就解釋了剛剛公式2和其中的參數是如何學習的,y_c,v_c 和 m_c 都是根據與目標中心距離決定的,通過轉化到對偶空間求的。
在這里,我們描述了如何學習殘差函數(2)中的自由參數,這些參數定義了判別損失(1)。我們的殘差函數包括標簽置信度 y_c ,空間權重函數 v_c ,和目標mask m_c ,此類變量通常是在當前的判別跟蹤器中手動構建的,但本文的方法是從數據中學習這些功能的。我們根據與目標中心的距離對它們進行參數化。這是由問題的徑向對稱性引起的,其中相對于目標的樣品位置的方向意義不大。另一方面,到樣品位置的距離起著至關重要的作用,特別是在從目標到背景的過渡中。
因此,我們使用徑向基函數 ** \\rho_k**,對 y_c,v_c 和 m_c 進行參數化,并學習它們的系數 ** \\phi _k** 。例如,位置 t \\in R^2 處的標簽 y_c 為:
y_c(t)=\\sum^{N-1}_{k=0}\\phi^y_k\\rho_k(||t-c||) \\tag{6}
我們使用函數:
\\rho_k(d)= \\begin{cases} max(0,1-\\frac{|d-k\\Delta|}{\\Delta}), & \\text {k 上述公式對應于結節位移為?的連續分段線性函數。注意最終情況 k=N-1 表示遠離目標中心的所有位置,因此可以同等對待。我們使用一個較小的值來實現目標背景過渡時回歸標簽的準確表示。類似地,分別使用系數 v_k 和 m_k 在(6)中對函數 v_c 和 m_c 進行參數化。對于目標mask m_c ,我們通過Sigmoid函數將值限制為間隔[0,1]。 圖3.學習的回歸標簽,目標mask和空間權重的圖。每個數量的初始化以虛線顯示。 訓練的時候是用多個圖片對訓練的 (M_{train},M_{test}) ,這些樣本是從同一個序列中抽樣出來的,對于給定的樣本對,先是用特征提取網絡提取到對應的特征 (S_{train},S_{test}) ,得到的特征輸入到D網絡中得到濾波器 f ,這個文章的目的就是學到一個可以推廣到沒見過幀的特征。然后在**S_{test}**上測試,然后計算一個損失: l(s,z)= \\begin{cases} s-z, & \\text {z>T} \\ max(0,s)), & \\text{z 這里就是之前提到的 Hinge-like 損失函數,T 表示前景和背景,所以這里只懲罰背景樣本。這里他們為了提升模型魯棒性,對每次迭代的損失都做約束,這就相當于一個中間的監督: L_{cls}=\\frac{1}{N_{iter}} \\sum^{N_{iter}}_{i=0} \\sum_{(x,c) \\in S_{test}} ||l(x*f^i,z_c)||^2 \\tag{9} 迭代次數也不是指定的,而是自適應的。上述公式中 z_c 是一個 mask 中心位于 bb 的中心的高斯函數,在 bb 回歸的地方,他們用了 IOUNet 來做。最終的損失函數為: L_{tot}=\\beta L_{cls}+L_{bb} \\tag{10} 對于給定的第一幀,他們用數據增強方式添加了15個樣本,然后用10次梯度下降來學習 f,在模型更新過程中,他們保持最新的50個樣本,每20幀更新一次。 給定帶有注釋的第一幀,我們采用數據增強策略來構建包含15個樣本的初始集合 S_{train} 。然后使用我們的判別模型預測架構 f=D(S_{train} ) 。得目標模型。對于第一幀,用10次梯度下降來學習。只要有足夠的置信度預測目標,我們的方法就可以通過向 S_{train} 添加新的訓練樣本輕松地更新目標模型。通過丟棄最早的樣本,保持最新的50個樣本。在跟蹤過程中,我們通過每20幀執行兩次優化器遞歸完成更新,或在檢測到干擾波峰時執行一次遞歸來更新目標模型。 我們的方法是使用PyTorch在Python中實現的。在單個NVidia GTX 1080 GPU上,當使用ResNet-18作為主干時,我們的跟蹤速度為57 FPS,對于ResNet-50為43 FPS。 學習更多編程知識,請關注我的公眾號: [代碼的路]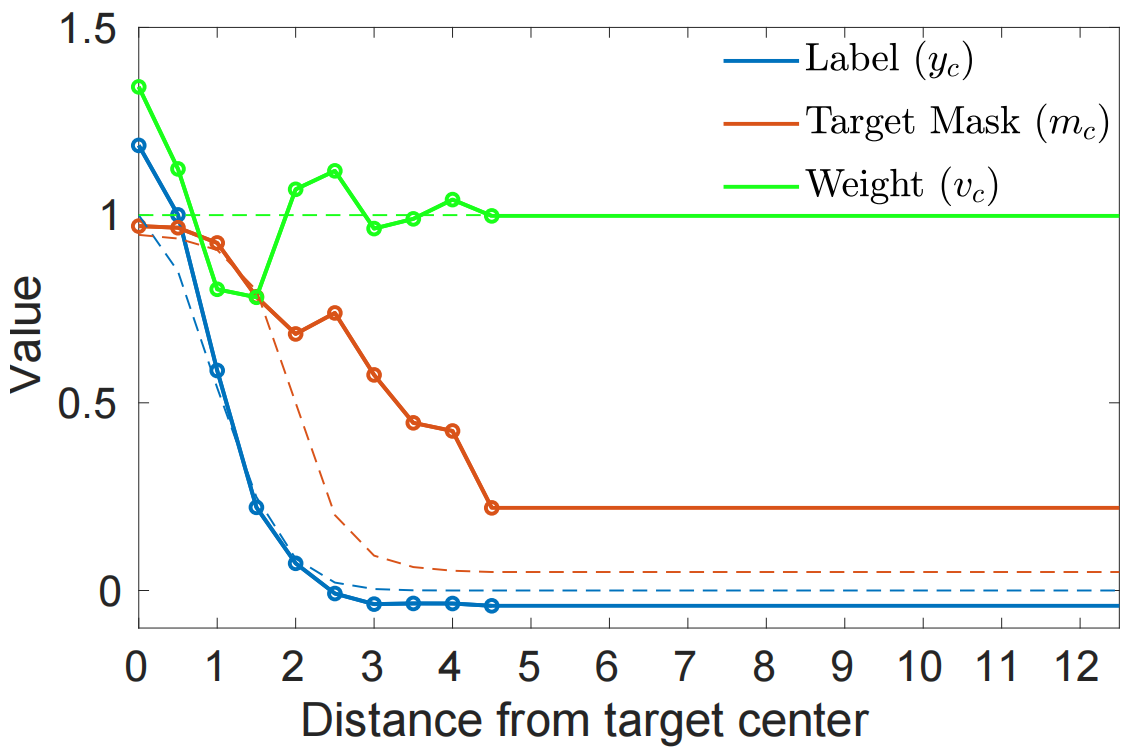
3.5 離線訓練
3.6 在線追蹤
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100719 -
機器視覺
+關注
關注
161文章
4369瀏覽量
120282 -
機器學習
+關注
關注
66文章
8406瀏覽量
132567 -
python
+關注
關注
56文章
4792瀏覽量
84628 -
pytorch
+關注
關注
2文章
807瀏覽量
13201
發布評論請先 登錄
相關推薦
Fast Intra-Prediction Model Selection for H.264 Codec
Ensemble Learning Task
什么是有限集模型預測控制
在BBNs的基礎上軟件殘留缺陷預測模型
自動跟蹤對稱電源:Tracking Regulated Po
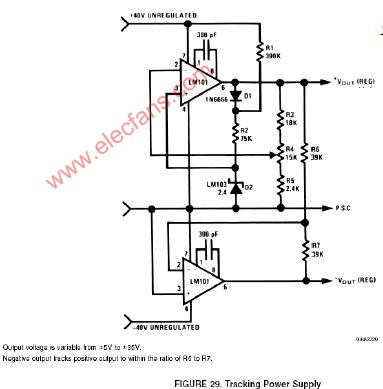
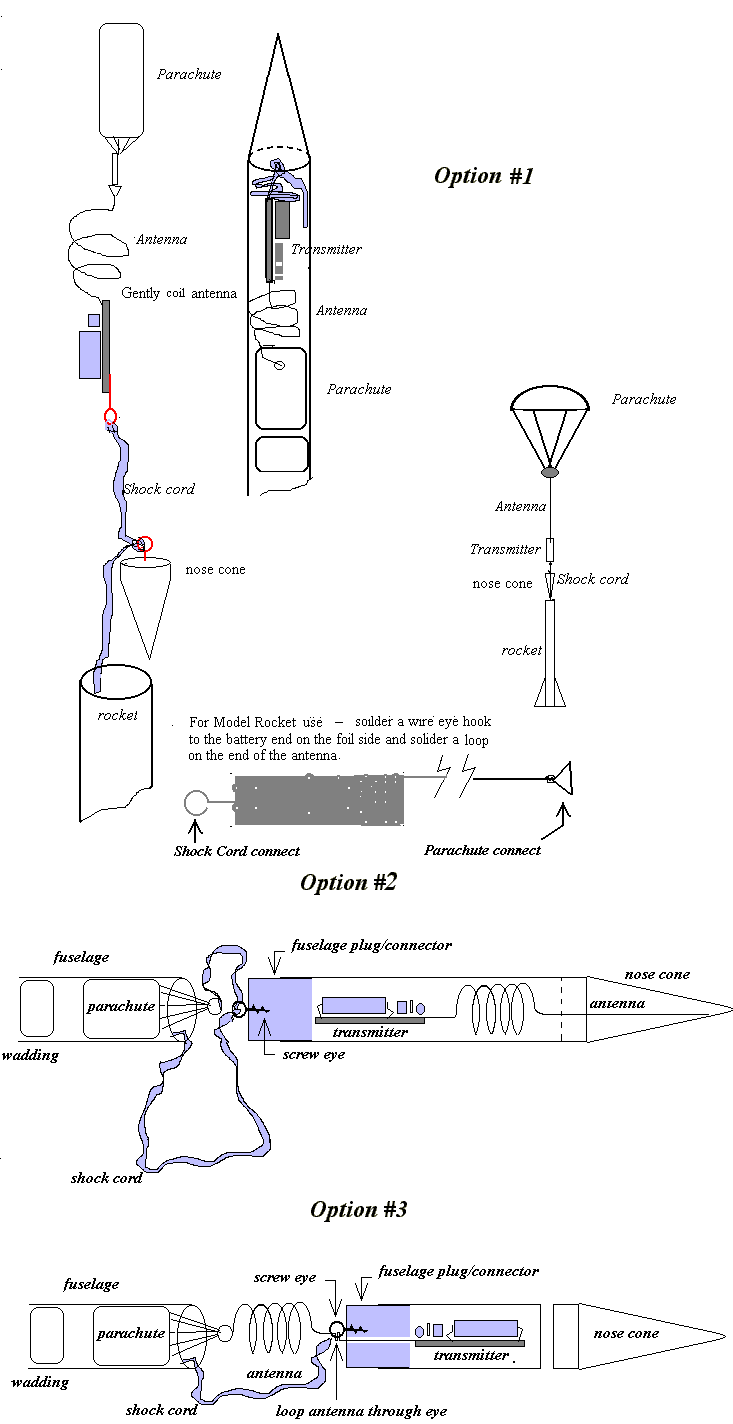
FM跟蹤發射器FM Tracking Transmitter
一種基于RNN的社交消息爆發預測模型
一種新穎的基于模型的機器學習方式——model based machine learning
機器學習中的無模型強化學習算法及研究綜述





 DIMP:Learning Discriminative Model Prediction for Tracking 學習判別模型預測的跟蹤
DIMP:Learning Discriminative Model Prediction for Tracking 學習判別模型預測的跟蹤










評論