【動態(tài)電路】的零狀態(tài)響應就是電路在零初始狀態(tài)下(動態(tài)元件初始儲能為零),由外施激勵源引起的響應,與零輸入響應不同的是,零狀態(tài)響應內(nèi)部儲能在初始狀態(tài)是零,就是儲能元件初始儲能為零,區(qū)分好這個后,就可以方便記住了,這期介紹RL電路的零狀態(tài)響應,同樣需要點一階線性微分方程的基礎!
關鍵詞:RL電路;零狀態(tài)響應;
01電路結(jié)構(gòu)
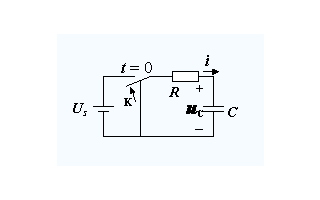
如圖1-1所示,是RL電路的結(jié)構(gòu):
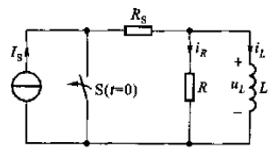
圖1-1 RL零狀態(tài)響應電路結(jié)構(gòu)
圖1-1所示為RL電路,直流電流源的電流為Is,在開關打開前電感L中電流為零,所以電感的初始條件為下:
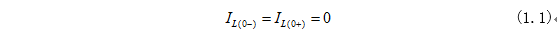
當電路穩(wěn)定之后,電感相當于導線,把電阻R進行短路了,所以時間在無窮后,電感的電流為:
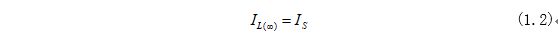
02分析思路
當開關S打開之后,電流源I對電感L就進行充電,電阻R兩端的電壓就是電感L兩端的電壓為:
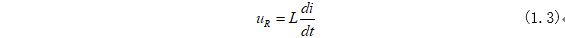
式(1.2)中電阻電壓為正的原因是因為電流流進電感,給電感進行儲能;上期“一階電路的零輸入響應——RL電路”同樣需要根據(jù)電流方向來進行分析。
根據(jù)KCL可求得節(jié)點電流公式為:
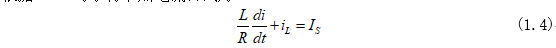
式(1.3)為非齊次微分方程,這里同“一階電路的零狀態(tài)響應——RC電路”一樣,進行省略步驟,電流iL的通解為:
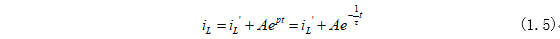
式(1.4)中右邊第一項表示非齊次微分方程的特解,第二項表示齊次微分方程的通解。
特解可以根據(jù)根據(jù)電路的初始狀態(tài)(1.1)代入式(1.5)進行求解為:
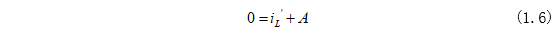
同時將電路穩(wěn)定狀態(tài)(1.2)代入代入式(1.5)進行求解為:
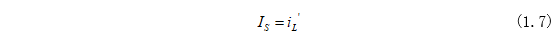
根據(jù)式(1.6)和式(1.7)可求得式(1.6)中系數(shù)A為:
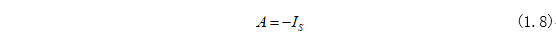
將式(1.7)和式(1.8)代入式(1.5)即可求得電路中電感電流為:
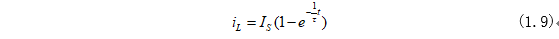
其中在開關S斷開之后,RL電路的時間常數(shù)為:
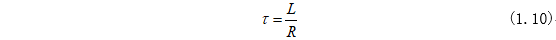
RL時間常數(shù)就是從電感L往外看的電路,將電流源斷路,電壓源短路后的等效電阻和自身電感比值的倒數(shù)。
將式(1.10)代入式(1.9)就可求得電感電流為:
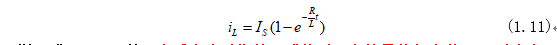
同樣,式(1.11)說明電感電流以指數(shù)形式趨近于它的最終恒定值Is,到達該值后,電壓和電流不再變化,電感相當于短路,電壓為零,此時電路達到穩(wěn)定狀態(tài)。
-
動態(tài)電路
+關注
關注
1文章
27瀏覽量
9658 -
一階電路
+關注
關注
0文章
30瀏覽量
13320 -
RL
+關注
關注
0文章
18瀏覽量
9823 -
RL電路
+關注
關注
0文章
7瀏覽量
6246 -
零狀態(tài)響應
+關注
關注
0文章
8瀏覽量
758
發(fā)布評論請先 登錄
二階網(wǎng)絡的零輸入響應和零狀態(tài)響應
線性系統(tǒng)的零輸入、零狀態(tài)及完全響應

一階RC電路的零輸入響應與零狀態(tài)響應的電路分析基礎實驗資料免費下載







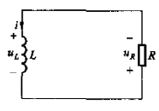











評論