對于新手來說，使用格雷碼做單目結構光三維重建是一個入門級的訓練。但是在復現時往往會遇到一個問題，明明解碼都很不錯了，重建后的點云精度卻很低，甚至重建出來的平面點云出現斷層現象。這是由于格雷碼是一種離散型編碼，編碼精度是整數級的像素，這種編碼設計注定了它的精度不會太高。所以在實際應用中，格雷碼通常是配合著其他編碼方式一起使用：比如使用格雷碼來標示相移的周期數。

盡管如此，由于格雷碼本身的特性，穩定性高，抗反光效果比較好，在精度需求不是特別高的情況下，還是有適用場景的。尤其是景深范圍大的時候，相位很容易出現模糊，可是對于黑白條紋的格雷碼適應的景深就能夠大一些。本文就簡單介紹下如何使用純格雷碼進行三維重建，并得到一個精度尚可的點云（至少不出現重建平面時明顯斷層/分層現象）。

從解決問題的本身出發，想要得到一個精度比較不錯的點云，最直觀的思路是解碼時得到一個準確的亞像素級精度，比如像相移那樣，但是對于格雷碼而言，很難去給出一個很好的插值函數去獲得一個亞像素級的匹配，實際上，如果以圖片某一行為例，你得到的解碼結果可能是 16,16,17,17,18，18,18，NaN，NaN，21… 對于這樣排列的解碼結果，想要用一個函數去定義亞像素的插值函數是一件很困難的事情，筆者暫時沒有看到哪篇文章提供了好的思路。(如果有讀者知道，歡迎和筆者溝通)。

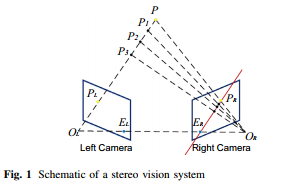
在無法獲得準確的亞像素級的解碼精度后，我們可以從三維重建方式本身去考慮,如上圖所示。圖中是一幅經典的雙目重建模型，在之前的系列篇中我們介紹了單目結構光重建可以使用雙目模型，只需要把投影儀看成一個逆相機就可以。圖中紅線即極線，也就是說，理論上相機成像點PL（圖中left camera） 對應的可能的投影儀（圖中Right Camra）中的位置是圖中紅線，如果知道對應的是圖中紅線哪一點，就可以解得準確的三維位置。

實際上，由于我們能夠解得的編碼只能是整數級的，導致我們的解碼結果會像如下圖所示的函數圖一樣，橙色的線是理論的極線，但是由于解碼的離散性，我們得到的解碼坐標是個整數級的數，如圖中的階躍函數，于是誤差就這么產生了。

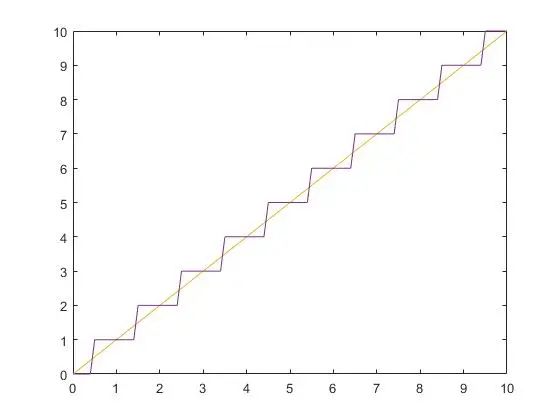
我們解得的點，通常會對應極線的或上方一點或下方一點，導致該點與投影儀中心點連線與相機像點和相機中心點發出的射線在三維空間不相交。如果相交，交點就是物體的在空間中的實際三維位置。盡管由于解碼的離散性導致兩條直線不相交，但是兩條這空間直線間的距離不會很遠，所以可以用如下思路去估計實際的物體三維位置：

求這兩條空間直線中距離最近的兩個點，而這兩個點的中點就是我們估計的物體三維位置點。

這兩個點怎么求呢？

在數學上很簡單，我們高中都學過如何求三維空間中兩條直線的距離，那條和兩條直線都垂直且相交的線與兩條直線的交點就是我們要求得的兩條直線在空間中距離最近的兩個點了！

至此，我們就很好的估計了一個比直接用解碼結果按公式求得的更準確的三維重建點了，但是細心的朋友一定發現了，在一般形式的結構光三維重建中，我們僅僅需要用到列方向的條紋，（為什么僅需要一個列方向，可以看系列篇之三維重建原理），但是在上述求射線的過程中，我們需要知道像點對應的投影儀位置的行和列兩個信息，如果僅有一個列方向的值，列所在的直線和原點就構成一個面了！那像點和相機中心連線的射線一定會和這個面有交點，且這個交點即是我們用傳統的解法得到的解，這個解通常由于列值（格雷碼）解碼值精度不夠而不夠精確。

純格雷碼的三維重建并不算很常見，如果一定要用，不防試下上述方法，可以保證一定精度，當然還是沒有相移法來的準確。還有一個顯然的缺點就是投影的圖片較多，需要行列方向都投影格雷碼，投影圖片數量太多會損失時間的效率，但是作為一個新手入門demo，還是很不錯的選擇！

審核編輯：劉清