正菜之前，我們先來了解一下圖（包括有向圖和無向圖）的概念。圖是圖論中的基本概念，用于表示物體與物體之間存在某種關系的結構。在圖中，物體被稱為節點或頂點，并用一組點或小圓圈表示。節點間的關系稱作邊，可以用直線或曲線來表示節點間的邊。

如果給圖的每條邊規定一個方向，那么得到的圖稱為有向圖，其邊也稱為有向邊，如圖10所示。在有向圖中，與一個節點相關聯的邊有出邊和入邊之分，而與一個有向邊關聯的兩個點也有始點和終點之分。相反，邊沒有方向的圖稱為無向圖。

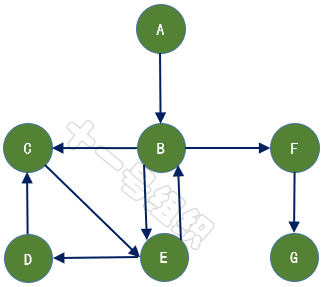
圖10有向圖示例

數學上，常用二元組G =（V，E）來表示其數據結構，其中集合V稱為點集，E稱為邊集。對于圖6所示的有向圖，V可以表示為{A，B，C，D，E，F，G}，E可以表示為{，，，，，，}。表示從頂點A發向頂點B的邊，A為始點，B為終點。

在圖的邊中給出相關的數，稱為權。權可以代表一個頂點到另一個頂點的距離、耗費等，帶權圖一般稱為網。

在全局路徑規劃時，通常將圖11所示道路和道路之間的連接情況，通行規則，道路的路寬等各種信息處理成有向圖，其中每一個有向邊都是帶權重的，也被稱為路網（Route Network Graph）。

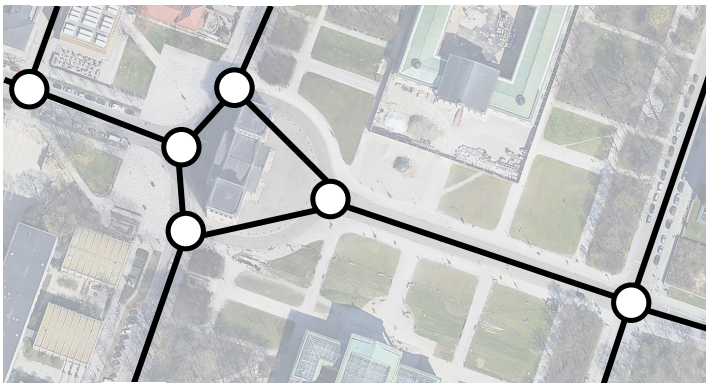
圖11道路連接情況

那么，全局路徑的規劃問題就變成了在路網中，搜索到一條最優的路徑，以便可以盡快見到那個心心念念的她，這也是全局路徑規劃算法最樸素的愿望。而為了實現這個愿望，誕生了Dijkstra和A*兩種最為廣泛使用的全局路徑搜索算法。

Dijkstra算法

戴克斯特拉算法（Dijkstra’s algorithm）是由荷蘭計算機科學家Edsger W. Dijkstra在1956年提出，解決的是有向圖中起點到其他頂點的最短路徑問題。

假設有A、B、C、D、E、F五個城市，用有向圖表示如圖12，邊上的權重代表兩座城市之間的距離，現在我們要做的就是求出起點A城市到其它城市的最短距離。

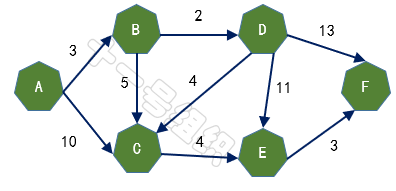
圖12 五個城市構建的有向圖

用Dijkstra算法求解步驟如下：

（1）創建一個二維數組E來描述頂點之間的距離關系，如圖13所示。E[B][C]表示頂點B到頂點C的距離。自身之間的距離設為0，無法到達的頂點之間設為無窮大。

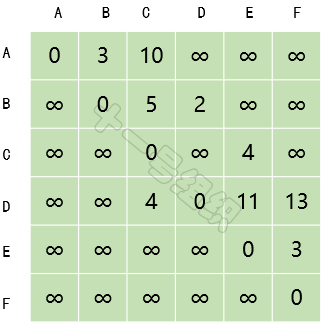
圖13 頂點之間的距離關系

（2）創建一個一維數組Dis來存儲起點A到其余頂點的最短距離。一開始我們并不知道起點A到其它頂點的最短距離，一維數組Dis中所有值均賦值為無窮大。接著我們遍歷起點A的相鄰頂點，并將與相鄰頂點B和C的距離3（E[A][B]）和10（E[A][C]）更新到Dis[B]和Dis[C]中，如圖14所示。這樣我們就可以得出起點A到其余頂點最短距離的一個估計值。

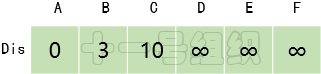
圖14 Dis經過一次遍歷后得到的值

（3）接著我們尋找一個離起點A距離最短的頂點，由數組Dis可知為頂點B。頂點B有兩條出邊，分別連接頂點C和D。因起點A經過頂點B到達頂點C的距離8（E[A][B] + E[B][C] = 3 + 5）小于起點A直接到達頂點C的距離10，因此Dis[C]的值由10更新為8。同理起點A經過B到達D的距離5（E[A][B] + E[B][D] = 3 + 2）小于初始值無窮大，因此Dis[D]更新為5，如圖15所示。

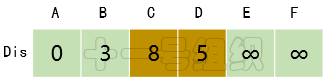
圖15Dis經過第二次遍歷后得到的值

（4）接著在剩下的頂點C、D、E、F中，選出里面離起點A最近的頂點D，繼續按照上面的方式對頂點D的所有出邊進行計算，得到Dis[E]和Dis[F]的更新值，如圖16所示。

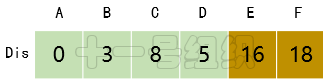
圖16 Dis經過第三次遍歷后得到的值

（5）繼續在剩下的頂點C、E、F中，選出里面離起點A最近的頂點C，繼續按照上面的方式對頂點C的所有出邊進行計算，得到Dis[E]的更新值，如圖17所示。

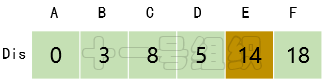
圖17 Dis經過第四次遍歷后得到的值

（6）繼續在剩下的頂點E、F中，選出里面離起點A最近的頂點E，繼續按照上面的方式對頂點E的所有出邊進行計算，得到Dis[F]的更新值，如圖18所示。

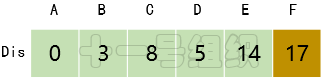
圖18 Dis經過第五次遍歷后得到的值

（6）最后對頂點F所有點出邊進行計算，此例中頂點F沒有出邊，因此不用處理。至此，數組Dis中距離起點A的值都已經從“估計值”變為了“確定值”。

基于上述形象的過程，Dijkstra算法實現過程可以歸納為如下步驟：

（1）將有向圖中所有的頂點分成兩個集合P和Q，P用來存放已知距離起點最短距離的頂點，Q用來存放剩余未知頂點。可以想象，一開始，P中只有起點A。同時我們創建一個數組Flag[N]來記錄頂點是在P中還是Q中。對于某個頂點N，如果Flag[N]為1則表示這個頂點在集合P中，為1則表示在集合Q中。

（2）起點A到自己的最短距離設置為0，起點能直接到達的頂點N，Dis[N]設為E[A][N]，起點不能直接到達的頂點的最短路徑為設為∞。

（3）在集合Q中選擇一個離起點最近的頂點U（即Dis[U]最小）加入到集合P。并計算所有以頂點U為起點的邊，到其它頂點的距離。例如存在一條從頂點U到頂點V的邊，那么可以通過將邊U->V添加到尾部來拓展一條從A到V的路徑，這條路徑的長度是Dis[U]+e[U][V]。如果這個值比目前已知的Dis[V]的值要小，我們可以用新值來替代當前Dis[V]中的值。

（4）重復第三步，如果最終集合Q結束，算法結束。最終Dis數組中的值就是起點到所有頂點的最短路徑。

A*算法

1968年，斯坦福國際研究院的Peter E. Hart, Nils Nilsson以及Bertram Raphael共同發明了A*算法。A*算法通過借助一個啟發函數來引導搜索的過程，可以明顯地提高路徑搜索效率。

下文仍以一個實例來簡單介紹A*算法的實現過程。如圖19所示，假設小馬要從A點前往B點大榕樹底下去約會，但是A點和B點之間隔著一個池塘。為了能盡快提到達約會地點，給姑娘留下了一個守時踏實的好印象，我們需要給小馬搜索出一條時間最短的可行路徑。

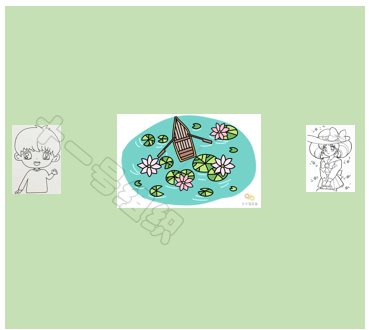
圖19 約會場景示意圖

A*算法的第一步就是簡化搜索區域，將搜索區域劃分為若干柵格。并有選擇地標識出障礙物不可通行與空白可通行區域。一般地，柵格劃分越細密，搜索點數越多，搜索過程越慢，計算量也越大；柵格劃分越稀疏，搜索點數越少，相應的搜索精確性就越低。

如圖20所示，我們在這里將要搜索的區域劃分成了正方形（當然也可以劃分為矩形、六邊形等）的格子，圖中藍色格子代表A點（小馬當前的位置），紫色格子代表B點（大榕樹的位置），灰色格子代表池塘。同時我們可以用一個二維數組S來表示搜素區域，數組中的每一項代表一個格子，狀態代表可通行和不可通行。

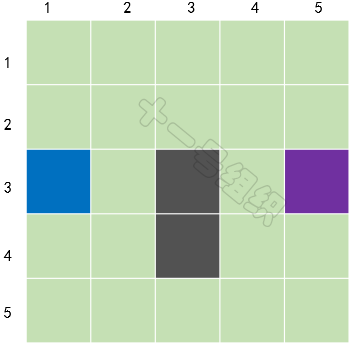
圖20 經過簡化后的搜索區域

接著我們引入兩個集合OpenList和CloseList，以及一個估價函數F = G + H。OpenList用來存儲可到達的格子，CloseList用來存儲已到達的格子。G代表從起點到當前格子的距離，H表示在不考慮障礙物的情況下，從當前格子到目標格子的距離。F是起點經由當前格子到達目標格子的總代價，值越小，綜合優先級越高。

G和H也是A*算法的精髓所在，通過考慮當前格子與起始點的距離，以及當前格子與目標格子的距離來實現啟發式搜索。對于H的計算，又有兩種方式，一種是歐式距離，一種是曼哈頓距離。

歐式距離用公式表示如下，物理上表示從當前格子出發，支持以8個方向向四周格子移動（橫縱向移動+對角移動）。

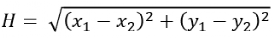
曼哈頓距離用公式表示如下，物理上表示從當前格子出發，支持以4個方向向四周格子移動（橫縱向移動）。這是A*算法最常用的計算H值方法，本文H值的計算也采用這種方法。

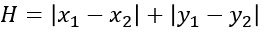
現在我們開始搜索，查找最短路徑。首先將起點A放入到OpenList中，并計算出此時OpenList中F值最小的格子作為當前方格移入到CloseList中。由于當前OpenList中只有起點A這個格子，所以將起點A移入CloseList，代表這個格子已經檢查過了。

接著我們找出當前格子A上下左右所有可通行的格子，看它們是否在OpenList當中。如果不在，加入到OpenList中計算出相應的G、H、F值，并把當前格子A作為它們的父節點。本例子，我們假設橫縱向移動代價為10，對角線移動代價為14。

我們在每個格子上標出計算出來的F、G、H值，如圖21所示，左上角是F，左下角是G，右下角是H。通過計算可知S[3][2]格子的F值最小，我們把它從OpenList中取出，放到CloseList中。

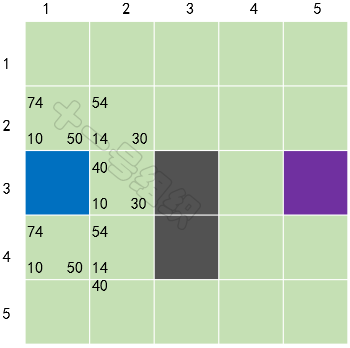
圖21 第一輪計算后的結果

接著將S[3][2]作為當前格子，檢查所有與它相鄰的格子，忽略已經在CloseList或是不可通行的格子。如果相鄰的格子不在OpenList中，則加入到OpenList，并將當前方格子S[3][2]作為父節點。

已經在OpenList中的格子，則檢查這條路徑是否最優，如果非最優，不做任何操作。如果G值更小，則意味著經由當前格子到達OpenList中這個格子距離更短，此時我們將OpenList中這個格子的父節點更新為當前節點。

對于當前格子S[3][2]來說，它的相鄰5個格子中有4個已經在OpenList，一個未在。對于已經在OpenList中的4個格子，我們以它上面的格子S[2][2]舉例，從起點A經由格子S[3][2]到達格子S[2][2]的G值為20（10+10）大于從起點A直接沿對角線到達格子S[2][2]的G值14。顯然A經由格子S[3][2]到達格子S[2][2]不是最優的路徑。當把4個已經在OpenList 中的相鄰格子都檢查后，沒有發現經由當前方格的更好路徑，因此我們不做任何改變。

對于未在OpenList的格子S[2][3]（假設小馬可以斜穿墻腳），加入OpenList中，并計算它的F、G、H值，并將當前格子S[3][2]設置為其父節點。經歷這一波騷操作后，OpenList中有5個格子，我們需要從中選擇F值最小的那個格子S[2][3]，放入CloseList中，并設置為當前格子，如圖22所示。

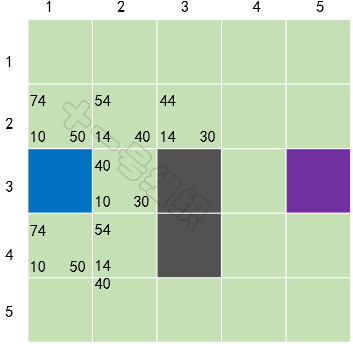
圖22第二輪計算后的結果

重復上面的故事，直到終點也加入到OpenList中。此時我們以當前格子倒推，找到其父節點，父節點的父節點……，如此便可搜索出一條最優的路徑，如圖23中紅色圓圈標識。

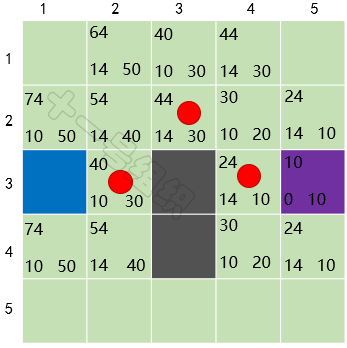
圖23 最后計算得到的結果

基于上述形象的過程，A*算法實現過程可以歸納為如下步驟：

（1）將搜索區域按一定規則劃分，把起點加入OpenList。

（2）在OpenList中查找F值最小的格子，將其移入CloseList，并設置為當前格子。

（3）查找當前格子相鄰的可通行的格子，如果它已經在OpenList中，用G值衡量這條路徑是否更好。如果更好，將該格子的父節點設置為當前格子，重新計算F、G值，如果非更好，不做任何處理；如果不在OpenList中，將它加入OpenList中，并以當前格子為父節點計算F、G、H值。

（4）重復步驟（2）和步驟（3），直到終點加入到OpenList中。

兩種算法比較

Dijkstra算法的基本思想是“貪心”，主要特點是以起點為中心向周圍層層擴展，直至擴展到終點為止。通過Dijkstra算法得出的最短路徑是最優的，但是由于遍歷沒有明確的方向，計算的復雜度比較高，路徑搜索的效率比較低。且無法處理有向圖中權值為負的路徑最優問題。

A*算法將Dijkstra算法與廣度優先搜索（Breadth-First-Search，BFS）算法相結合，并引入啟發函數（估價函數），大大減少了搜索節點的數量，提高了搜索效率。但是A*先入為主的將最早遍歷路徑當成最短路徑，不適用于動態環境且不太適合高維空間，且在終點不可達時會造成大量性能消耗。

圖24是兩種算法路徑搜索效率示意圖，左圖為Dijkstra算法示意圖，右圖為A*算法示意圖，帶顏色的格子表示算法搜索過的格子。由圖24可以看出，A*算法更有效率，手術的格子更少。

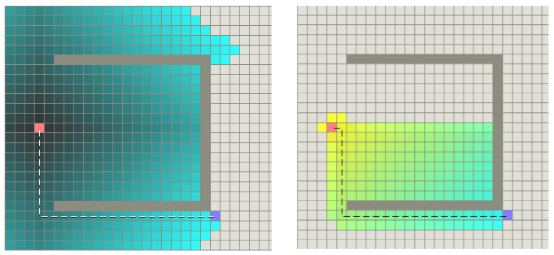
圖24 Dijkstra算法和A*算法搜索效率對比圖（圖片來源：https://mp.weixin.qq.com/s/myU204Uq3tfuIKHGD3oEfw）

審核編輯 ：李倩