步進電機概述：

步進電機驅動器的細分原理介紹，步進電機安裝有帶永久磁性的轉子，而定子至少具有兩個繞線。當轉子磁性與定子繞線保持一致時，將驅動第二個繞線。兩個繞線交替開啟和關閉，這將導致電機鎖定在想要的步進位置。通過繞線的電流方向還可反向。在帶有兩個定子繞線的步進電機中，有四個步進以 90 °隔開。步進電機驅動器的細分原理介紹，根據向定子繞線提供的脈沖，可精確控制步進電機移動的步進。步進電機的速度控制可通過向繞線提供脈沖頻率實現，而旋轉方向可通過反向脈沖序列進行更改。電機內部的極片有許多齒，有助于定位相對于定子的轉子位置。一些步進電機的定子級也有齒。根據使用的控制技術，可全步進、半步進或微步進控制步進電機。簡單的方形脈沖可以控制處于全步進的電機，而先進控制技術（如脈寬調制 (PWM)）可用于微步進。步進電機驅動器的細分原理介紹，在國內，大家對細分還不是特別了解，有的只是認為，細分是為了提高精度，其實不然，細分主要是改善電機的運行性能，現說明如下：步進伺服電機的細分控制是由驅動器精確控制步進電機的相電流來實現的，以二相電機為例，假如電機的額定相電流為3A，如果使用常規驅動器（如常用的恒流斬波方式）驅動該電機，電機每運行一步，其繞組內的電流將從0突變為3A或從3A突變到0，相電流的巨大變化，必然會引起電機運行的振動和噪音。如果使用細分驅動器，在10細分的狀態下驅動該電機，電機每運行一微步，其繞組內的電流變化只有0.3A而不是3A，且電流是以正弦曲線規律變化，這樣就大大的改善了電機的振動和噪音，因此，在性能上的優點才是細分的真正優點。由于細分驅動器要精確控制電機的相電流，所以對驅動器要有相當高的技術要求和工藝要求，成本亦會較高。需要注意的是，國內有一些驅動器采用平滑來取代細分，有的亦稱為細分，但這不是真正的細分，一定要分清兩者的本質不同。

步進電機驅動器的細分1．平滑并不精確控制電機的相電流，只是把電流的變化率變緩一些，所以平滑并不產生微步，而細分的微步是可以用來精確定位的。步進電機驅動器的細分2．電機的相電流被平滑后，會引起電機力矩的下降，而細分控制不但不會引起電機力矩的下降，相反，力矩會有所增加。步進電機驅動器的細分原理介紹，步進電機安裝有帶永久磁性的轉子，而定子至少具有兩個繞線。當轉子磁性與定子繞線保持一致時，將驅動第二個繞線。兩個繞線交替開啟和關閉，這將導致電機鎖定在想要的步進位置。通過繞線的電流方向還可反向。

全步和半步：步進驅動器控制步進電機的運行方式，步進電機常用的勵磁模式有全步、半步和微步三種。這些勵磁模式對電機提供的運行特性和扭矩都有影響。每次將輸入脈沖施加到電機時，步進電機都會將電子信號轉換為機械運動。每個脈沖以固定增量移動軸。如果步進電機的步進分辨率為1.8°，那么為了讓軸旋轉一整圈，在全步進操作中，步進電機需要接收200個脈沖，360°÷1.8=200。 有兩種全步勵磁模式： 在單相全步中，電機一次僅在一個相通電的情況下運行。在任何激勵模式中，這種模式需要來自驅動器的最少功率。

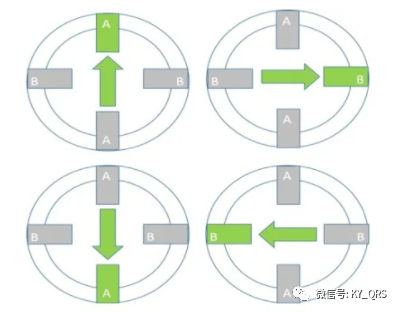
在雙相全步中，電機在兩相同時通電的情況下運行。此模式提供了改進的扭矩和速度性能。兩相開啟比單相開啟提供大約30%到40%的扭矩，但它需要來自驅動器的兩倍功率。

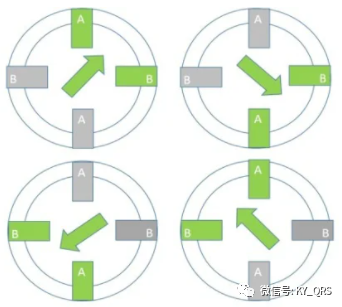
半步勵磁模式是一相開啟和兩相開啟全步模式的組合。這導致基本步距角的一半。由于角度分辨率的提高，這個較小的步距角提供了更平滑的操作。半步產生的轉矩比兩相全步低約15%，但修改后的半步通過增加單相通電時施加到電機的電流來消除轉矩降低。

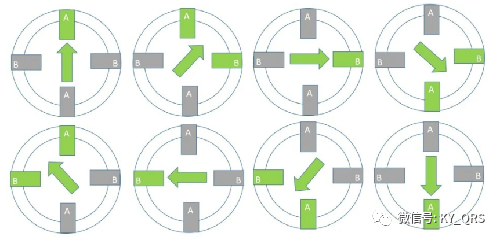
微步可實現更好的控制和更平穩的操作： 微步可以將電機的基本步長分割多達256倍，使小步距變小。微型驅動器使用兩個相隔90°的電流正弦波，這非常適合實現電機的平穩運行。您會注意到電機運行安靜，沒有真正可檢測到的步進動作。

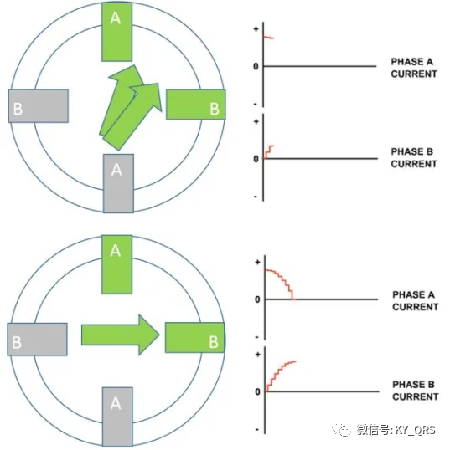
通過控制每個繞組中電流的方向和幅度，分辨率提高，電機特性改善，振動更小，運行更平穩。因為正弦波一起工作，所以從一個繞組到另一個繞組的平滑過渡。當一個電流增加時，另一個電流減小，從而實現平穩的步進進展并保持扭矩輸出。 細分的原理和輸出控制：

一個理想的步進電機電流曲線應該是相位相差90度的正弦曲線如下圖：

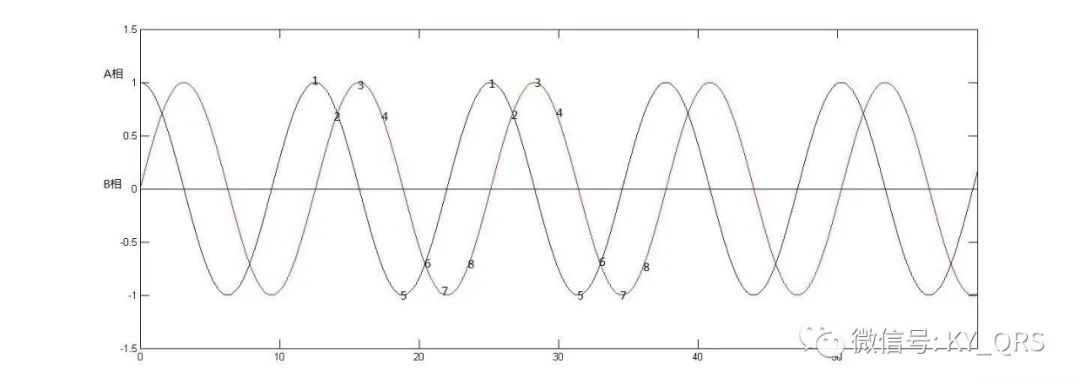
圖中藍色線時A相電流，紅色線是B相電流。如果把A相正負極值視為A+A-，B相正負極值視為B+B-，比較一下四拍方式正轉A+B+A-B-和反轉A+B-A-B+不難看出四排方式實際上是用一個脈沖來代替一個正弦半周期，相位點從左到右變化則電機正轉，從右到左電機反轉。類似的我們把八拍方式A+;A+B+;B+;B+A-;A-;A-B-;B-;B-A+;放到曲線里也可以找到對應點，圖中標出了各拍的相位點1，2，3…，不難看出用A+B+代替第2拍點用B+A-代替第四拍點都是近似的做法。那么這種近似和理想情況的電流的差值去哪里了呢？這些電流被無謂的消耗掉了而且多余的電流會引起電機轉動的不平穩。為什么要細分呢？實際細分的終極目標就是在正弦的周期中插入若干個點使得相電流接近正弦變化，細分可以提高定位精度和電機運轉的平穩性。

spwm運算和輸出 Spwm的產生可以分為軟件方法和硬件方法，硬件方法通過硬件產生一路三角波一路正弦波，經過一個比較器比較正弦波幅值與三角波幅值的關系即可得到spwm波。這種方法也應用于很多spwm集成芯片。硬件方法在波形產生上不需要軟件參與，并且調頻和調幅控制上都是比較簡單的。硬件方法的功能和性能取決于芯片本身，對于比較復雜的應用上會受到限制。 軟件方法的思路是使得pwm波以spwm的脈寬數據變化濾波后就可以得到正弦波形，通過計算得到占空比的波形數據，按波形數據調整pwm。其實軟方法和硬方法也并不是絕對的，比如ti的dsp芯片內部的spwm發生器，他的做法是在內存中存儲一張正弦表，然后用一個和定時器時鐘同步的計數器正負計數模擬一個三角波，每個時鐘將正弦表的值與三角計數值作比較輸出即得到spwm，實際上可以看成是一種半軟件半硬件的做法。軟件方法的優勢在于成本低且更靈活，成本低不用說了，靈活性上舉個例子：調制正弦波性的極性是由獨立的控制位實現的（雙極性），如果輸出標準的正弦波形硬方法需要三角波發生器和正弦波發生器的起始點精確對齊，這在硬件電路實現上需要附帶鎖相環電路才能保證，而軟件方法則不需要任何附加操作。現在為了改善步進電機的驅動性能，我們希望極性翻轉點落后輸出幾個微秒，要做到這一點硬件方法改動肯定是難上難，而軟件方法上只需要增加個定時滯后輸出就行了。 為了減少運算開銷也可以使用查表法，把計算好的spwm數據存儲在rom里，按順序輸出表中的值即可。這種方法的數據計算可以在pc機上通過matlab軟件進行，將數據算好粘貼到源程序中就可以了。查表法的局限在于參數的變化和存儲開銷的矛盾，參數越復雜占用存儲空間越大。 (1)三角波向鋸齒波的轉換 載波為三角波時輸出的是一個左右不對稱的pwm波形，只有這種波形能夠調制出半周期對稱的正弦波，這種方法稱為非對稱的自然采樣法。其它方法（規則采樣等效面積…）都是為了減小計算量或不得以而采取的近似方法。非對稱pwm開點與關閉點沒有必然關系，必須由中央對齊的pwm模式通過一個周期的兩次更新來輸出。三角波可以看成是兩個鋸齒波的組合，因此我們可以通過鋸齒波的數據來簡化程序結構。我們比較下面三張圖：

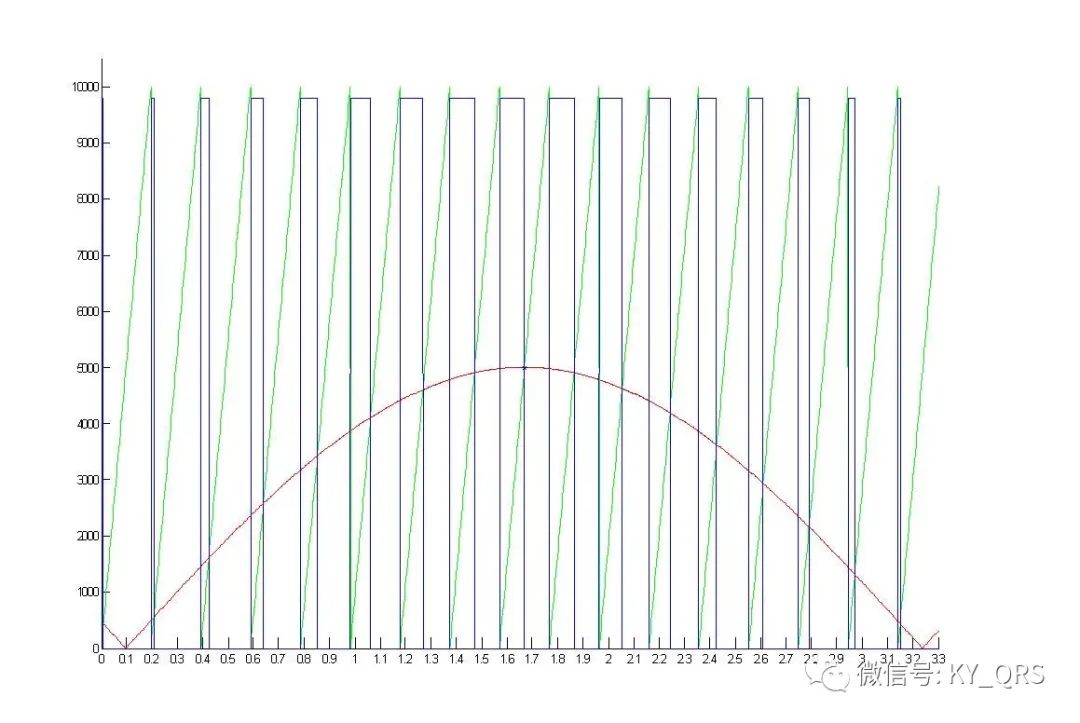
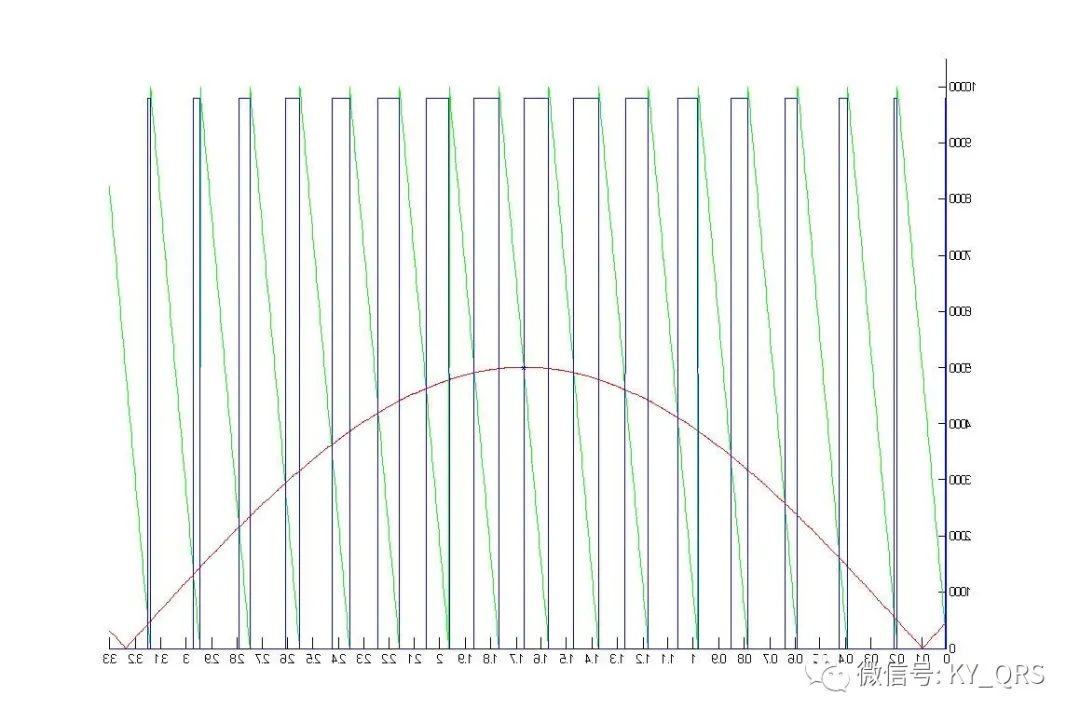
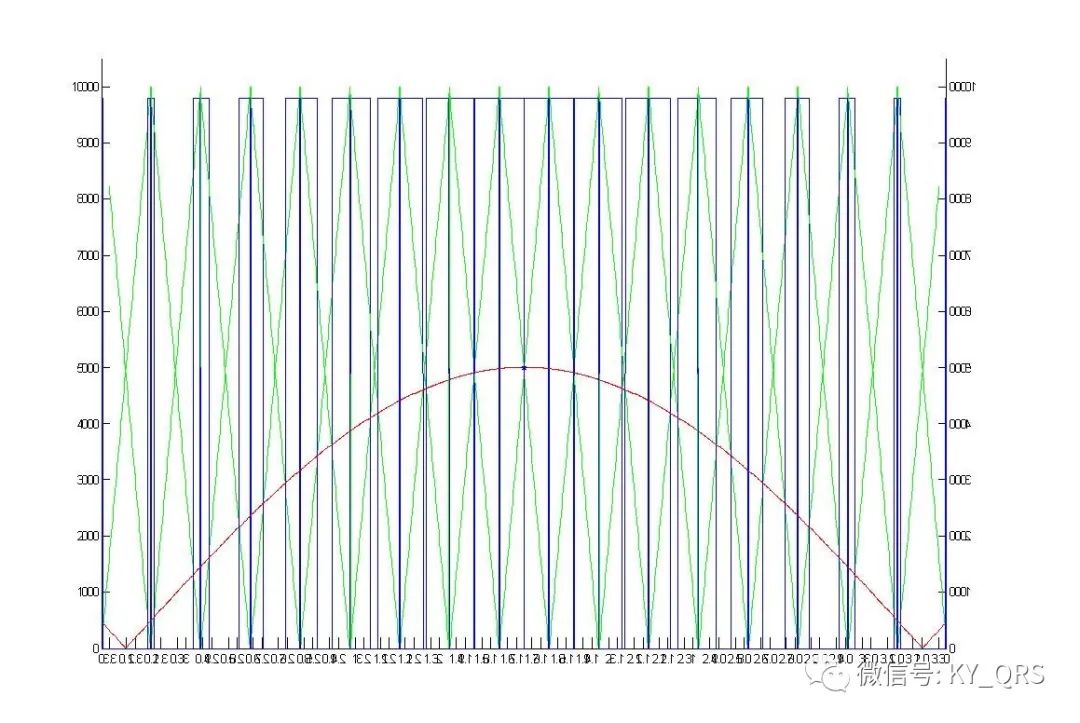
圖1是一個鋸齒波幅值為1，載波比N=16，正弦幅值0.5，正弦與鋸齒波相差為半個鋸齒波周期；圖2是圖1水平翻轉的結果；圖3是圖1和圖2的疊加結果。圖三中看到三角波形的spwm數據了嗎？沒錯就這么簡單，鋸齒波正弦幅值比為2：1，相差半個鋸齒波周期，計算出來的數據首尾組合成三角波數據。算法上就很簡單了，假設數組中存放上述的鋸齒波spwm數據，編號0~15共16個，依次取0，1，2，…15為三角波形開點輸出數據，則反向取15，14，13，…0為三角波形關點數據即可。特別的如果載波比為奇數時三角波也為奇數，中間的數自然和自己組合的數據仍然是正確的。 注意這里提及的方法可以把三角波形的計算轉換為鋸齒波，但并不能減少計算量，因為如果是偶數個三角波只要計算四分之一周期就夠了其他的是對稱的，而鋸齒波形數據需要計算半個周期。至此我們可以使用鋸齒波的方法計算按三角波的數據輸出。 (2)spwm迭代運算 為計算spwm占空比首先要求得鋸齒波斜線與正弦交點，即方程KX+B=Y與Sin(X)=Y的解。這個方程是一個超越方程，只能通過迭代的方法計算。我們將直線方程變為X=(Y-B)/K，首先任取一個X值（這個值就是迭代初值），將它帶入Sin(X)求一個Y值再將Y值代入(Y-B)/K求一次X值，再將X帶入Sin(X)求一個Y值…如此反復若干次后可以得到一個結果就是方程式的解，這個就叫做迭代法。迭代次數越多；迭代初值越接近結果精度越高。每一組數據計算有這樣幾個參數1：正弦幅值（三角幅值與之成比例）2：載波比N值即半周期中三角波個數。另外pwm的占空比即定時器的通道值是和pwm的周期值有關系的，因此為了計算定時器通道值還需要一個周期值，對于stm32f這個值就是定時器ARR寄存器的值，它決定pwm周期（或頻率）。附件中有個matlab_spwm.rar，matlab下計算定時器spwm數值和繪圖的小工具上面幾個圖就是用它畫的，開始部分可以置參數 s_M=32768/65536 %正弦波幅值比0~1 s_N=16 %半周期三角波個數 s_Pre=16384 %單片機定時器模數值 執行分為三部分，計算spwm數據；將數據按周期值換算為定時器設定值；畫圖；
計算定時器設定結果在TimerSetting中，復制粘貼替換tab字符成逗號就行了，下面是上述參數的計算結果： 1780 5246 8444 11221 13461 15088 16063 16384 16075 15182 13764 11893 9645 7102 4346 1463 (3)spwm實時運算的優化 如前所述簡單的應用查表法就可以解決了但是復雜一點的功能就不能滿足要求了，比如步進電機大范圍調速、不同轉速下恒力矩輸出、恒加速運動等等。網上有很多文章介紹自然采樣法的數學方法，并給出了各種優化算法，這些算法力圖精確求解三角方程與正弦方程的交點，由于運算中帶有大量的浮點運算若沒有dsp或高速浮點處理芯片的支持必然會造成運算時間過長對實時調控產生影響。實際上我們需要的計算精度和每載波周期可能的開關點數量有關系，此數值用C來表示，稱其為控制比數值上=載波周期/pwm周期，同步調制方式中此值為整數，可以理解為用多少個pwm周期控制一個載波周期。pwm頻率實際上是開關電路的極限頻率或最理想工作的頻率，假設每載波周期可能的開關點數量為512個則需要二進制的9位計算精度如果再加一位存疑位最多計算10位就夠了。如果采用數據類型IEEE32浮點數迭代運算將得到24位（二進制）精度的計算結果，與實際需要相差甚遠,也就是說你算了半天大部分是沒有意義的計算,這種計算資源浪費發生在每一次運算中,因此累計起來就比較驚人了。從另一個角度看由于pwm頻率的限制有高精度的計算結果也無法實施高精度的開關控制,這么說就好理解了。對計算采取一定的優化是必須的它將直接影響系統的實時性能。 步進電機運行控制 至此假設我們可以很快的在單片機上進行實時的迭代運算了。迭代計算一個半周期的spwm其輸入的原始參數只和三個數值有關:
1.M正弦的幅值這個值將決定步進電機的相電流大小,也就是步進電機的輸出力矩。步進電機的優點之一是它的低速性能,當步進電機低速運轉時轉子始終受到磁場力的牽引轉動,這個力的大小直接取決于勵磁電流的大小,很小的速度下卻可以用很大的力牽引轉動。而直流電機的低速運動只能靠減小勵磁電流實現,實際上就是小力矩實現低速,這樣控制就不可能很精確特別是啟停階段尤其麻煩。步進電機在高速時力矩下降很快這個原因也不難理解,因為在步進電機勵磁線圈里有多組磁極快速劃過產生很大的感生電動勢抵消了驅動的電壓致使勵磁電流變小力矩變小。為了改善高速性能解決辦法只有一個提高工作電壓。根據電機轉速自動調整相電流的大小就可以實現恒定的力矩輸出了,即低轉速小幅值高轉速大幅值。 2.載波比N和控制比C,這兩個參數和調制頻率F的關系是: F*2C*2N=TF(TF是定時器的時鐘頻率) 我們慢慢來解釋一下這個式子,調制頻率就是我們實際想要的電機轉速,從上面式子可以看出要讓電機速度增加有兩個方法即減小C或減小N(TF也是可以變的暫不考慮); C實際上就是定時器的模數值(ARR),他的含義是使用幾個定時器時鐘周期產生一個pwm周期,前面的2是由于定時器工作在中央對齊模式下,定時器+-計數一輪產生一個完整的三角波周期。ARR的取值范圍不可以太小,因為需要定時器中斷來更新個通道的值,太小的數值兩次更新時間過短而無法實現計算和更新步計數等操作。ARR的值如果太大則輸出的pwm頻率過低效果不佳。 N是載波比也就是半周期的三角波的數量,他的含義是使用幾個pwm周期調制出一個正弦周期,其實也就是我們常說的細分數,它決定一個正弦周期(一個步距角)內可以控制的位置點的數量。在常見的驅動器中這個數值都是由撥碼開關事先設定的,工作中是一個固定值,原因是硬件電路無縫的調整細分度幾乎是不可能的。軟件運算則沒有這個問題,N的取值可以是任意的，唯一受影響的就是極性控制，上面算式里N前面的2含義是正弦正半周期和負半周期。N的取值還要考慮內存和計算占用；迭代算法如果有接近結果的初始值將使得運算效率大幅提高，因此對于有初始值的運算每一個計算點都要有存儲空間占用，過大的N值要考慮內存資源，如果無初值的計算則要考慮計算資源。特別的當N值變化時初值會與真實值有差距，所以應盡量減少N的變動。 步值計數產生AB極性邏輯和正反轉：
先來梳理一下目前已經現在做到的內容，內存中有一個數組存放整個正弦半周期的實時運算的spwm數據，這個數據是根據當前的pwm周期折算過，因此每個pwm周期依次將數組內容賦值給定時器通道值就可以在定時器通道管腳輸出正弦變化的pwm了。另外使用一個（l6205是兩個，也可以用非門）io口來控制極性輸出，比如高電平輸出正弦負半周，低電平輸出正弦正半周。
接下來需要安排一個合理而簡單的數據結構把步進計數、細分和極性控制合為一體。首先我們用一個s32 stepcounter全局量來做步進計數,它的數值與步進電機的實時位置對應，這個變量是一個很關鍵的變量，因為任意時刻的AB兩相spwm數據輸出點和極性控制信號都由它產生。假設我們把它的低八位視為細分步計數（256為最大細分）,則這個計步值除256對應整步位置。另外安排一個u8 microstep用來控制細分步進,它的取值和當前的細分度有關，如果256細分則microstep=1,128細分microstep=2,以此類推.如果電機正轉前進一個微步則stepcounter+=microstep，如果反轉一個微步則stepcounter-=microstep（微步進這部分可以放到中斷程序里），OK正反轉很簡單，微步前進自動更新整步。關鍵點在于如何使用這個計數值產生兩個相位的極性信號輸出控制和A相B相的spwm數據位置，這里解釋一下為什么會希望控制都由這一個變量產生：因為這樣的程序最簡單，雖然這里講一大堆但是在編程實現時你就看到了就幾行搞定；不容易出錯，效率最高，你可以想象的到如果涉及的變量越多操作的代碼越多需要考慮的可能性越多也越容易錯；便于封裝和功能擴展，比如你想做一個AD采樣值與電機位置按一個比例同步的程序即轉滑阻電機跟著動的小玩意兒，稍微改改把AD采樣值賦給計步值其它都不用管了。
先說第一個數據的輸出，spwm數組256個，如果不考慮極性則數據位置只和stepcounter的低8位有關，因此A相數據用stepcounter的低8位作指針從數組取數就可以（A相0值點為計步0值點），B相與A相相差為90度，所以A=0，1，2，255，0 則B=128，129，130，127，128能看出來嗎？（A的數據指針+128）%256等同于 A的數據指針^128就是B的數據指針。
程序上這樣寫：
A通道值=spwm數組[（u8）stepcounter]；
B通道值=spwm數組[（u8）stepcounter^128]；
這里數組大小是256，所以一個邏輯異或就解決，如果你非要取大小是100個的話你就得（point+50）%100才能找到B相位點了。 步進電機基本算法，S算法：

為了實現步進電機的平緩啟停以及避免轉高轉速時不失步停轉。在步進電機啟動、停止過程中，需要采用加減速的算法對啟動過程進行控制。S曲線是加減速控制最理想的方案。但是S曲線的公式以及控制過程都比較復雜。

將S曲線離散化，在整個加減速過程中，以一定的時間間隔更新頻率，總的更新次數為2*N，i表示為第i次的更新，則第i次更新的頻率f(i)表示為：

其中fb為開始的頻率，fr是最終運行的頻率，α是曲線的伸縮系數，一般可以取3-5之間的常數。

比如，啟動加速，開始頻率為400Hz，運行頻率為5KHz。

停止減速，開始頻率為5KHz，停止頻率為400Hz，

加減速的時間均為1s，按10ms的時間間隔更新頻率，總共更新100次，α取5。

通過以下步驟實現實現步進電機的S曲線的加減速控制：

配置1ms的定時器以及1ms的中斷程序在中斷程序中對加減速的頻率更新次數i進行計數配置產生步進電機驅動信號的PWM模塊，設置PWM的定時中斷以及中斷程序在PWM的定時中斷程序中，計算當前更新次數對應的頻率，并按出來的頻率更新PWM的頻率以及占空比在PWM的定時中斷程序中，計算步進電機運行的步數，如果達到設置的步數減去停止的S曲線減速運行所設置的步數，則開始減速運行。同時檢測外部輸入，如果有需要停止運行的輸入條件，則開始減速運行。

整個加減速控制過程的難點在于：

步進電機的計步以及頻率更新需要在每一個PWM中斷中進行。步進電機的運行頻率最高到40KHz，這種頻率下，PWM的定時中斷周期達到了25us，PWM定時器中斷程序運行總時間盡量小，根據經驗至少小于中斷周期的30%，即7.5us。一旦超過這個數值，導致所有中斷程序（包括PWM定時中斷程序）漏運行，基本主程序無法運行，導致整個控制器假死現象。根據S曲線的公司是一個復雜的非線性的指數浮點數運算，需要耗費大量的時間，直接調用C語言的庫函數計算這一數值可能耗費幾十上百毫秒。

為了解決S曲線的運算時間問題，基于STM32F103，我采用了查表法，具體步驟如下：

1. 將α值定義5，

的取值范圍為-5~5之間。

2. 在整個加減速過程中，表達式

在取值范圍-5~5內均勻取1024個數值，得到數值表。

3. 定義一個unsigned short型有1024個元素的const類型的數組，用于存儲數值表。

4. Const數組存儲在內部的flash，數值表共占用2048字節。

STM32F103RTC6共256K，程序組和設置參數占用48K，bootloader程序占用了8K，遠程升級空間占用了100K，目前應用程序只用到40K左右。

剩余60K左右的空間，騰出2K的空間來存儲數值表，有空間，就是這么任性。

5. 在中斷程序中，根據總的更新次數以及當前的更新計數值，計算

值，再映射到0-1023的數值有的索引值，通過索引獲取數值。

6. 需要注意的是stm32f103不支持浮點數的運算，所以對于浮點數的運算，需要換算成乘以一個數再除以另一個數，比如*α，需要轉變為*65535/13107。

下面一段代碼是根據更新的計數值獲取頻率的函數：

U16 fnMC_GetFreq(U16 n, U16 halftn, U16 alpha, U16 minfreq, U16 maxfreq){//alpha=alpha * 4096

signed int udataA;

signed short uiDataA;

U16 uiRes;

U32 uwData;

udataA=(signed int)alpha * (signed int)n;

udataA=(signed int)udataA / halftn;

if(udataA > 32767){

udataA=32767;

}

uiDataA=(signed short)alpha - (signed short)udataA;

uiDataA=(signed short)4 * 4096 - uiDataA;

if(uiDataA < 0){

uiDataA=0;

}

uiRes=(U16)uiDataA;

uiRes=uiRes / 32;//*1023/8/4096

if(uiRes > 1023){

uiRes=1023;

}

udataA=(signed int)(maxfreq - minfreq) * g_mc_uchExp[uiRes];

udataA=udataA / 65535;

uiDataA=(signed int)udataA;

uiDataA +=minfreq;

if(uiDataA < 200){

uiDataA=200;

}

return(uiDataA);

}

下面一段代碼是產生步進電機控制信號的PWM周期中斷程序：

int data;

U16 freq;

STRMotorRegs *motor;

motor=&g_motor_regs[0];

MOTOR_A_CLEARINT();

motor->steps ++;

data=(int)MOTOR_A_STEPS_GET();

if(motor->direction==0)

{

data=data + 1;

}

else

{

data=data - 1;

}

MOTOR_A_STEPS_SET(data);

freq=motor->runfrequency;

if(motor->runstate==MOTOR_RUN_STATE_INC){

if(motor->runtimer >=motor->starttime){

motor->runstate=MOTOR_RUN_STATE_IDLE;

}else{

freq=fnMC_GetFreq(motor->runtimer, motor->halfstarttime, motor->alpha, motor->startfreq, motor->runfrequency);//U16 n,U16 halftn,U16 alpha,U16 maxfreq,U16 minfreq)

}

motor->runsnapfreq=freq;

}else if(motor->runstate==MOTOR_RUN_STATE_IDLE){

if(motor->totalstep <=(motor->steps + motor->stopremainstep)){

motor->runstate=MOTOR_RUN_STATE_DEC;

motor->runtimer=0;

}

motor->runsnapfreq=freq;

}else{

if(motor->runtimer >=motor->stoptime){

freq=motor->stopfreq;

}else{

freq=fnMC_GetFreq(motor->runtimer, motor->halfstoptime, motor->alpha, motor->runsnapfreq, motor->stopfreq);//U16 n,U16 halftn,U16 alpha,U16 maxfreq,U16 minfreq)

}

}

if(motor->steps >=motor->totalstep)

{

motor->starting=FALSE;

}

if(FALSE==motor->starting)

{

MOTOR_A_DISABLE();

}else{

motor->curfrequency=freq;

fnMT_Cal_MotorA_TimeConf();

}

下面是生成S曲線數值表、控制步進電機啟動、停止的視頻，從視頻上可以明顯看到啟動時慢加速->快加速->慢加速的過程，以及停止時慢減速->快減速->慢減速的過程。

部分程序代碼（需要代碼可以下載完整程序）

審核編輯 ：李倩