本文中以一款新型雙電機耦合系統電動汽車(dual-motor coupling-propulsion electric vehicle,DMCP-EV)為研究對象,制定了基于PSO算法系統效率優化的驅動模式控制策略,在滿足動力性要求的基礎上提高了整車經濟性。
1 雙電機耦合動力系統模型
1.1 雙電機動力系統構型介紹
該款新型耦合驅動系統如圖1所示。在該耦合驅動構型中,電機M1與太陽輪S相連,電機M2與連接器T相連。制動器L1與太陽輪S同軸,當L1閉合時,太陽輪被固定,電機M1停止運行。制動器L2與齒圈R相連,當L2閉合時,齒圈R固定。減速齒輪G1與齒圈R相連,當連接器T位于右端時,三者相連接,隨電機M2的運轉而運行;當連接器T位于中間時,電機M2關閉;當連接器T位于左端時,兩電機轉矩在太陽輪C處耦合。
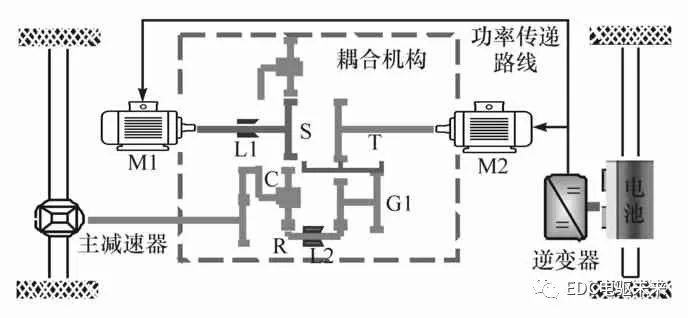
圖1 新型雙電機耦合系統構型
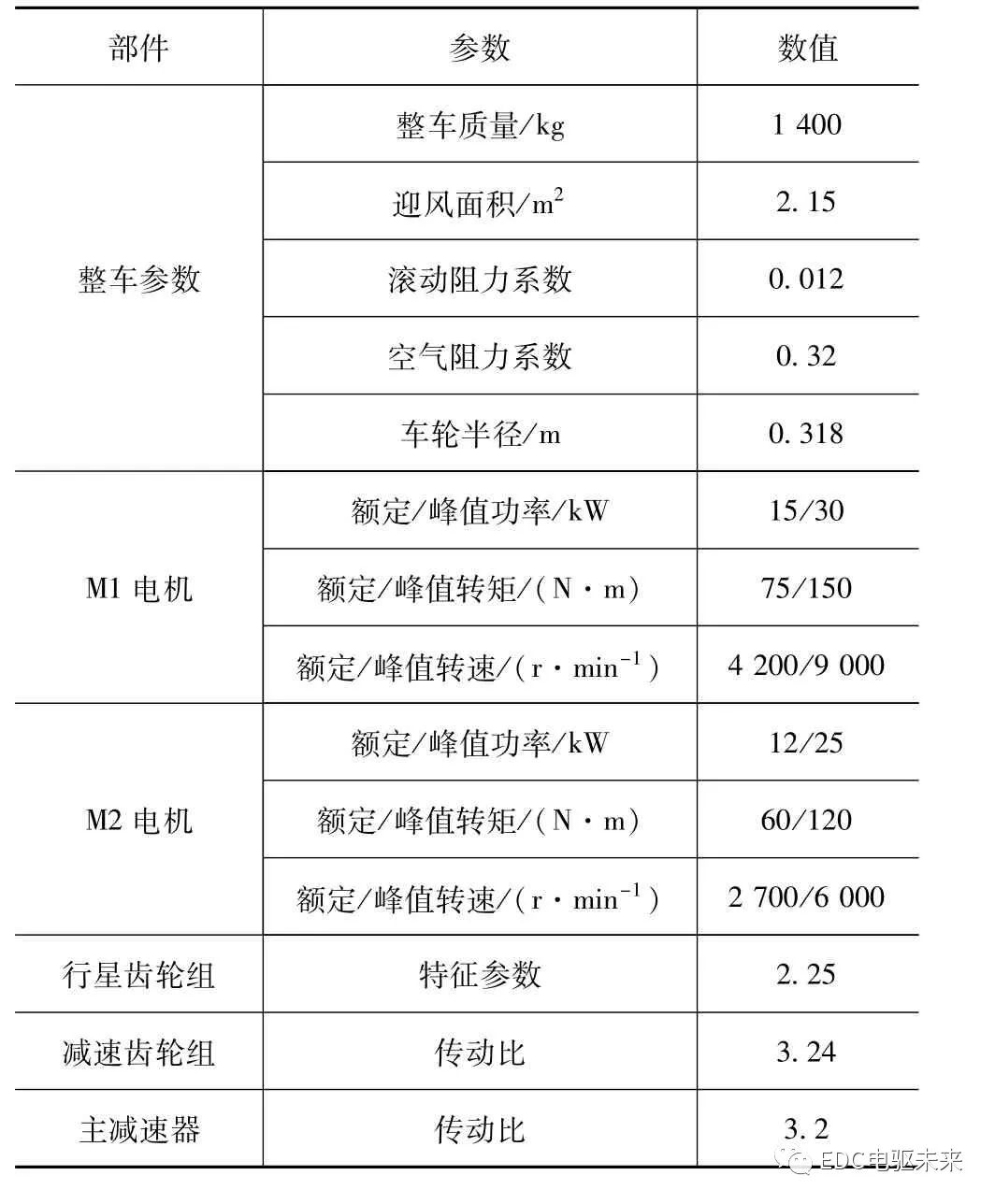
當汽車正常行駛時,整車控制器接受并處理來自傳感器的信號,向電機控制器等執行器發出指令,通過控制連接器T及制動器L1、L2的開閉,使動力系統工作在不同的工作模式:電機M1單獨驅動模式(定義為SM1)、電機M2單獨驅動模式(定義為SM2)、雙電機轉矩耦合模式(定義為TC)、雙電機轉速耦合模式(定義為SC)以及再生制動模式。由于本文重點研究的是驅動系統的驅動性能,故在此暫不考慮再生制動的控制。本文中所研究的某款純電動汽車的具體動力部件參數見表1。
表1 EV動力部件參數
1.2 雙電機動力系統建模
1.2.1 工作模式分析
當制動器L1斷開,L2閉合,且連接器T位于中間位置時,電機M1工作,M2關閉,系統處于電機M1單獨驅動模式,則SM1系統動力學模型為
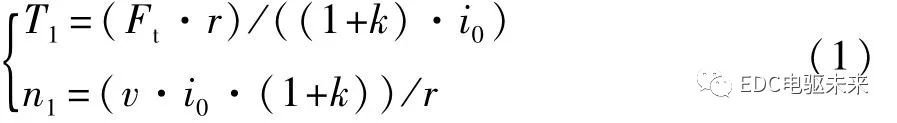
式中:n1為電機M1的轉速;T1為電機M1的轉矩;r為車輪半徑;k為行星架特征參數;i0為主減速器傳動比;F t為驅動力;v為車速。
當制動器L1閉合,L2松開且連接器T位于右端時,電機M1停止,M2運轉,功率經減速齒輪、行星架輸出。此時為電機M2單獨運行模式,SM2模式系統動力學模型為
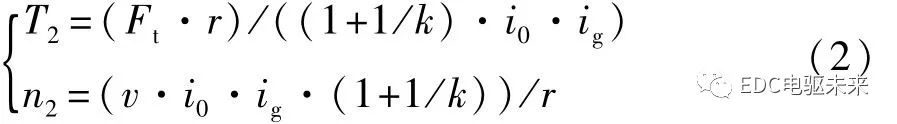
式中:i g為減速齒輪組的傳動比;n2為電機M2的轉速;T2為電機M2的轉矩。
當制動器L1斷開,L2閉合,且連接器T位于左端時,兩個電機的轉矩在太陽輪處耦合,經行星架傳遞到車輪,驅動汽車行駛。系統處于雙電機轉矩耦合模式TC,此時的系統動力學模型為
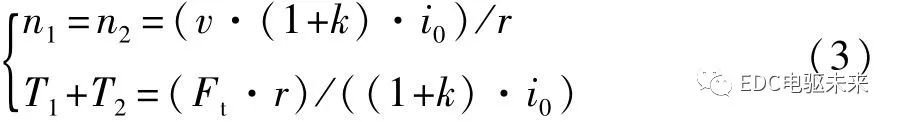
當制動器L1、L2斷開,連接器T位于右端時,兩電機轉速在行星架處耦合,動力經行星架傳遞到車輪,驅動汽車行駛。系統處于雙電機轉速耦合模式,此時系統動力學模型可表示為
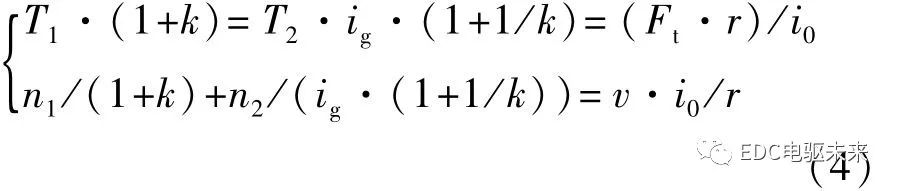
1.2.2 系統效率建模
不同模式下的系統效率數學模型為
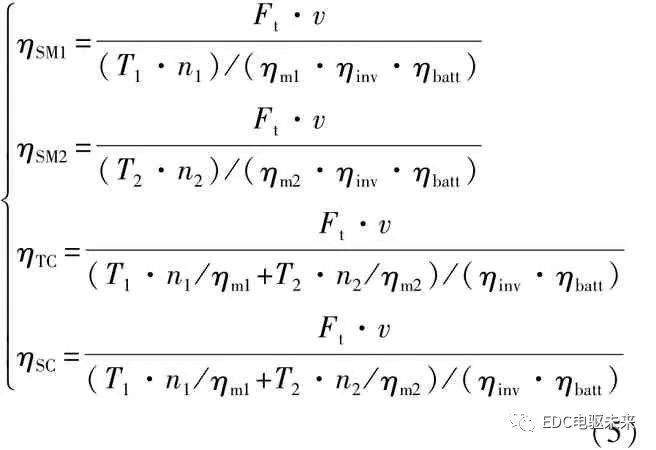
式中:ηSM1、ηSM2、ηTC、ηSC分別為 SM1、SM2、TC、SC模式下的系統效率;ηinv為逆變器效率。
約束條件為
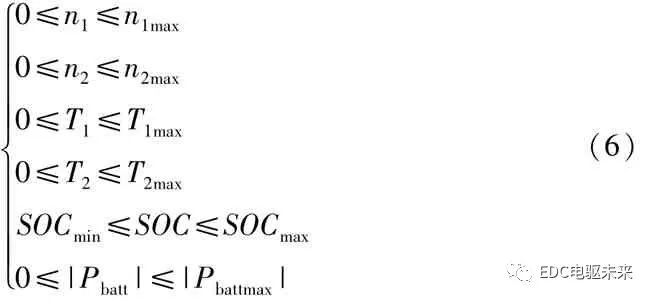
式中:n1max、n2max分別為電機 M1、M2的最大轉速;SOC min為電池組最小荷電狀態;SOC max為電池組最大荷電狀態;P battmax為當前SOC對應的最大放電功率。
2 驅動系統模式劃分與控制策略
2.1 不同模式工作范圍的劃分
基于上述分析可知,DMCP-EV具有4種驅動模式。在動力需求的約束下,整車控制器根據獲得的實時行駛速度、加速度信號、驅動電機的工作特性以及各個模式的工作原理,獲得各個模式的工作范圍。對各個模式工作范圍的劃分流程如圖2所示,可簡述如下,首先由車載傳感器采集到速度、加速度信號,然后根據各個模式的動力學模型以及速度等信息,計算各個模式在該工況下所需要的電機轉矩、轉速,則可以獲得各個模式的有效工作范圍,如圖3所示。
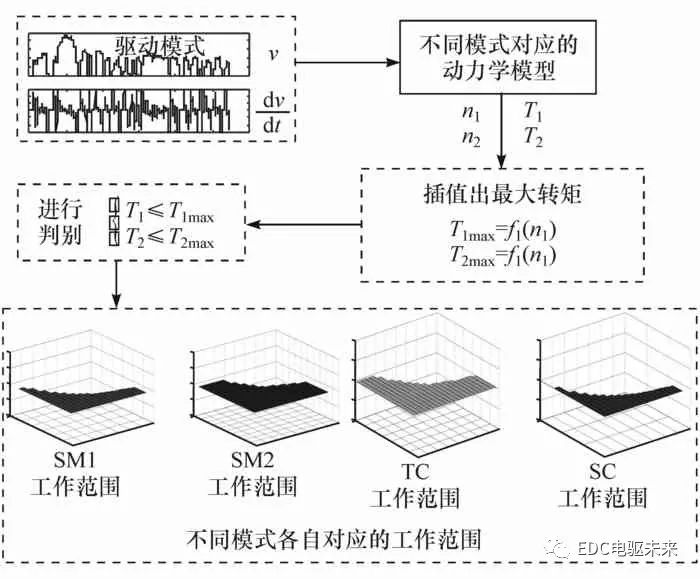
圖2 不同模式工作范圍劃分流程
2.2 基于PSO算法的耦合模式下系統效率優化
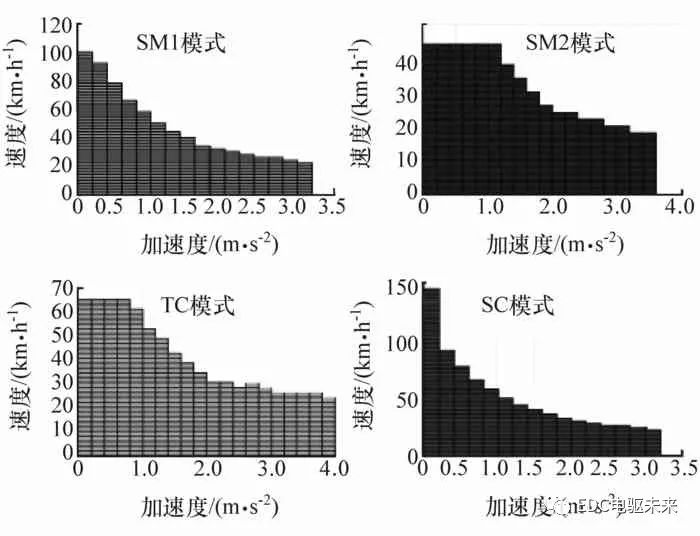
圖3 不同模式下的有效工作范圍
依據以上各模式工作范圍的劃分,滿足當前速度、加速度以及駕駛員需求的工作模式可能有多種。為提高經濟性,采用PSO優化各模式的系統效率,并根據當前行駛工況選擇效率最優的工作模式。據此,本文中制定基于PSO系統效率優化的雙電機耦合驅動系統控制策略,其框架如圖4所示。控制策略是根據當前工況選擇效率最優工作模式,具體步驟如下:
(1)判斷滿足當前工況的工作模式的情況;若僅有一個適合的模式,則選擇該模式;若存在多個驅動模式,則進入系統效率優化控制模式;
(2)計算滿足當前工況的各個工作模式系統效率,其具體計算過程詳見1.2.2節;
(3)選擇系統效率最高的工作模式作為當前工作模式以提高整車經濟性。
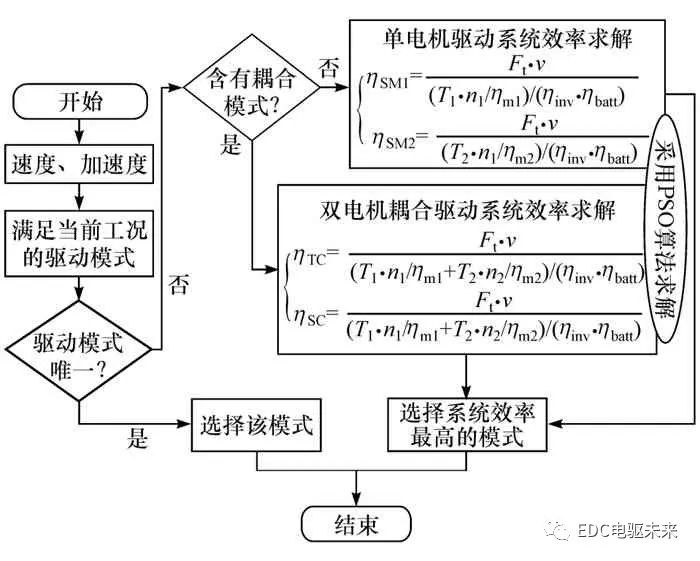
圖4 基于粒子群算法的模式劃分及控制流程
2.2.1 TC模式下的系統效率優化
TC模式下,兩電機的轉速與車速成比例,兩電機的轉矩相耦合,可以在約束范圍內進行調節。采用粒子群優化算法優化兩電機的轉矩分配,以獲得系統最優效率。PSO算法初始參數和系統效率流程如圖5所示。TC模式系統效率優化過程為:給定速度和加速度,通過粒子群優化算法獲得電機M1、M2的目標轉矩,使系統效率ηTC達到最優。優化模型如下。
目標函數(適應度函數):

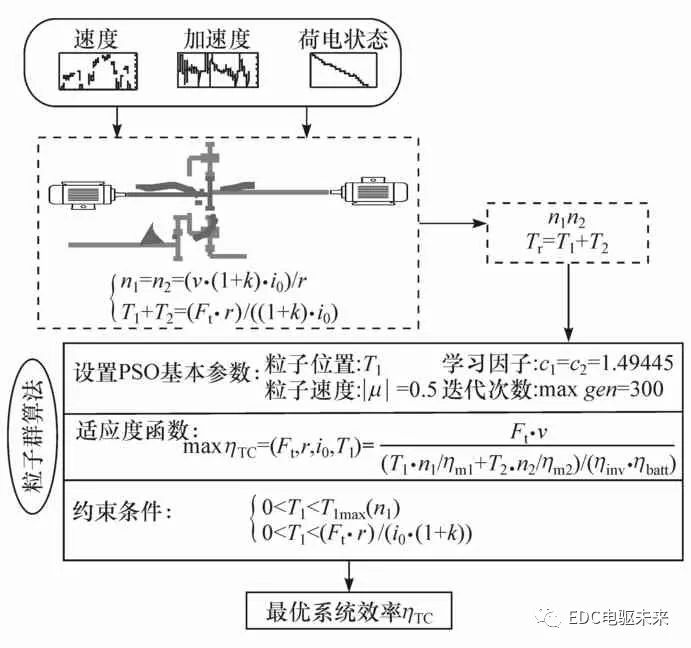
圖5 粒子群算法優化系統效率流程圖
約束條件:
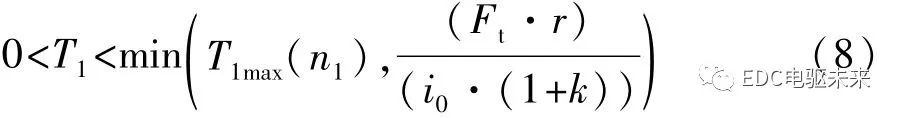
選取M1電機的轉矩T1作為控制變量,則其相應粒子的位置為

式中:i為粒子編號;j為迭代次數。
系統效率尋優結果如圖6所示。由圖可以看出,系統效率在第40代左右收斂至最優值。TC模式下的最優轉矩分配如圖7所示。
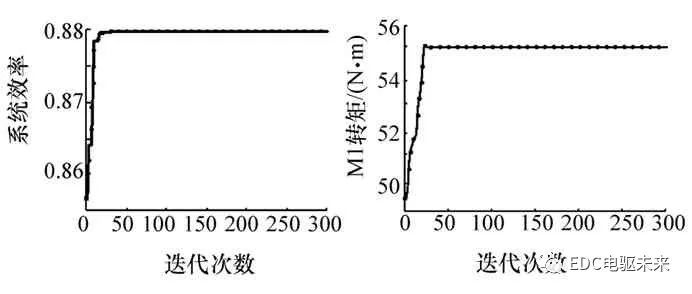
圖6 PSO算法尋優迭代圖
2.2.2 基于系統效率優化的模式控制
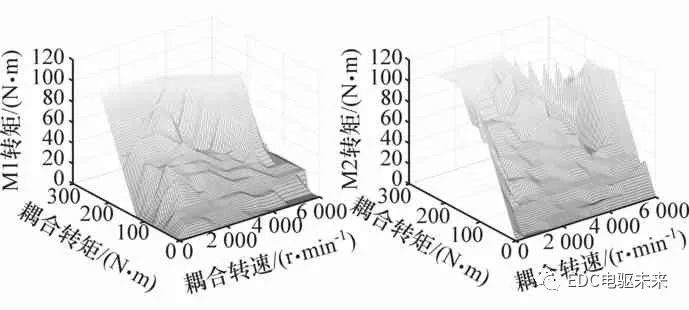
圖7 TC模式下的最優轉矩分配
在SC模式下,兩電機的轉矩與驅動力矩成比例,兩電機的轉速相耦合,可以在約束范圍內調節。與TC模式類似,SC模式獲取最優系統效率關鍵是合理分配兩電機的轉速。同樣采用粒子群算法優化,具體求解過程與TC模式類似。圖8為SOC=0.9時優化后不同模式下的系統效率。適合當前工況的最佳驅動模式可通過比較該工況下4種驅動模式的系統效率而得出,即可以獲得4個工作模式的工作邊界,如圖9(a)所示。為減少計算量并提高整車控制器工作效率,提前劃分了各個工作模式的工作邊界,如圖9(b)所示。并將結果制成表格存儲在控制器中,通過查表獲得當前最優工作模式。
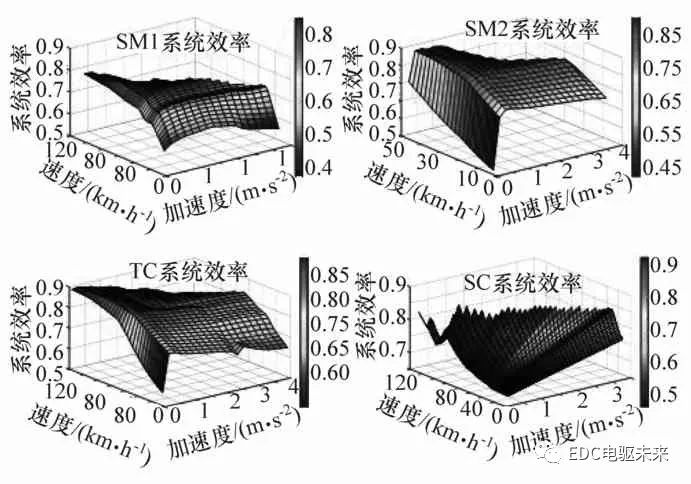
圖8 SOC為0.9時不同模式下的系統最優效率
3 仿真與試驗驗證
3.1 PSO優化前后仿真驗證
在Matlab/Simulink環境下實現裝備該新型雙電機耦合驅動系統的整車模型的搭建,通過優化前后結果對比來驗證所提出的基于PSO系統效率優化的模式劃分及選擇策略的有效性。為體現對比結果的公正性,未經PSO效率優化的系統的模式劃分方法與本文相同,模式的選擇同樣基于瞬時最優的原則,該模式選擇策略分別實時計算當前工況下4種工作模式的需求功率,選取需求功率最小的模式作為當前工況下的工作模式。兩者在城市道路循環UDDS下進行仿真,結果如圖10(a)所示。由圖可見,在整個工況過程中,實際車速很好地跟隨目標車速。驅動時,該系統基于所提出的控制策略,自動匹配適合當前工況的工作模式,從而在滿足車輛動力性能需求的同時,保證了較低的能耗。圖10(b)和圖10(c)示出該系統優化前后的工作模式隨UDDS工況切換的情況,“1~4”分別表示 SM1、SM2、TC、SC工作模式。
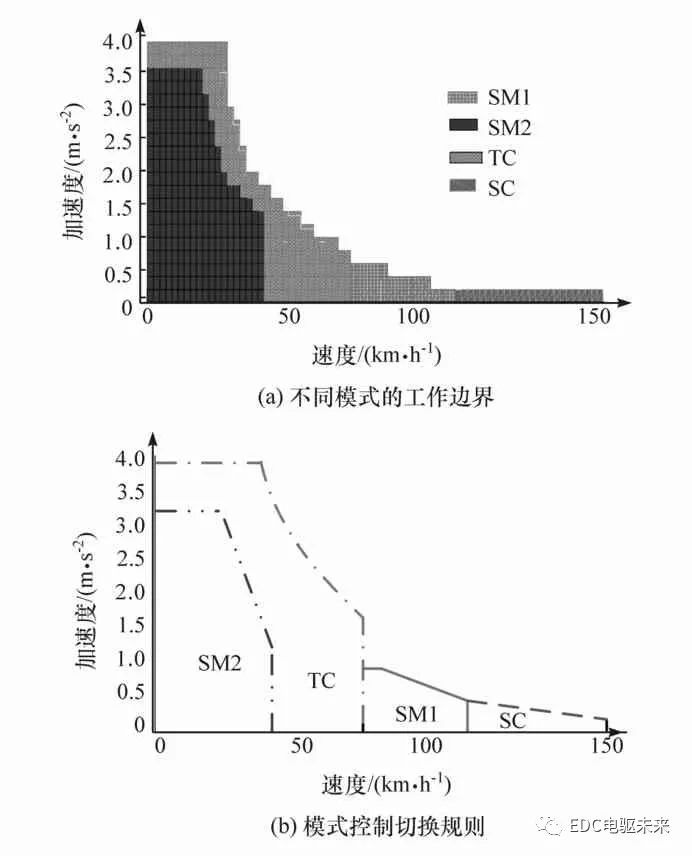
圖9 不同模式的工作邊界
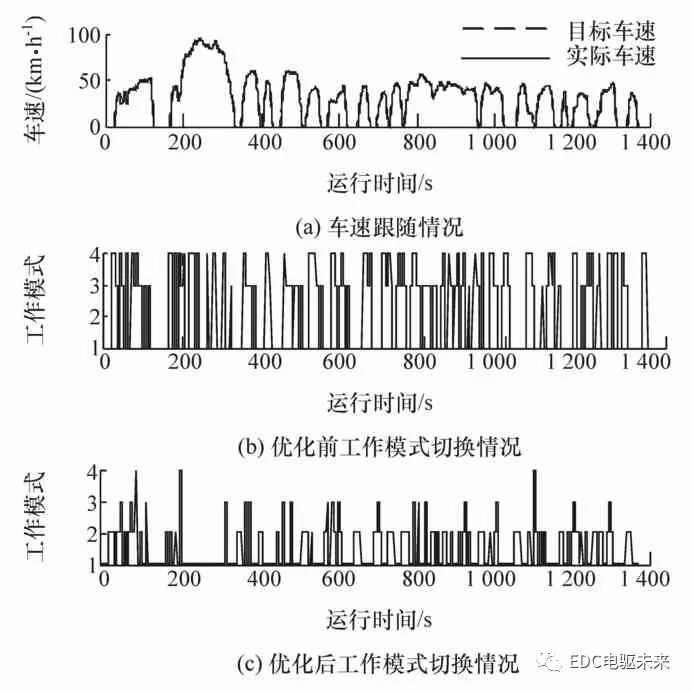
圖10 車速跟隨情況和優化前后的工作模式切換情況
圖11給出了該系統PSO優化前后的兩電機的轉矩和轉速。可以看出,優化前后的M1、M2電機轉矩和轉速分配變化明顯。圖12為優化前后的電機轉矩以及轉速的對比。可以看出,經優化重新分配轉矩轉速后,該系統的SOC變化范圍縮小,能耗從優化前的1.165降低為1.036 kW·h,降低了11%左右,達到了提高整車能量經濟性的目的。
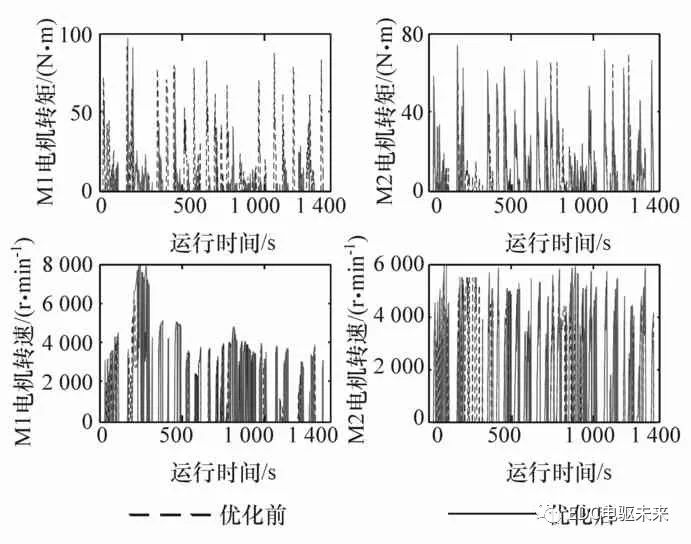
圖11 優化前后的M1、M2電機轉矩轉速對比
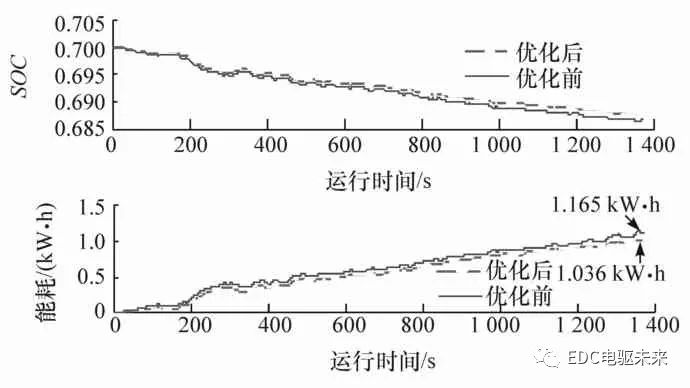
圖12 優化前后的SOC和能耗對比
3.2 基于PSO系統優化前后臺架試驗驗證
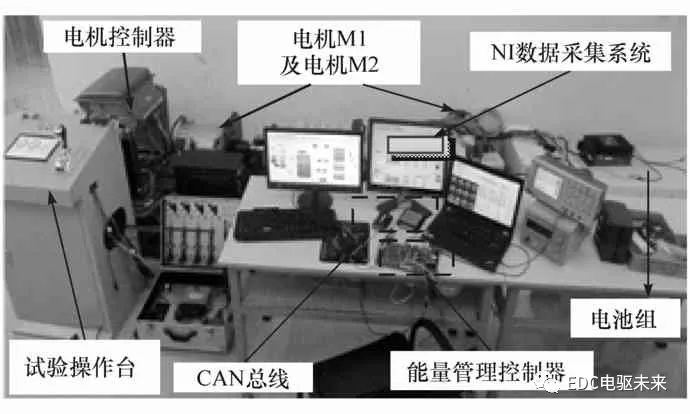
圖13 臺架試驗實物圖
為驗證PSO系統效率優化的實際效果,基于雙電機耦合驅動系統試驗平臺(圖13)進行臺架試驗。選用飛思卡爾MC9S12EQ512汽車級微處理器作為該試驗平臺的主控制器主芯片。采用CAN總線進行數據通信,波特率設為250 kbps,采用J1939應用協議。使用LabVIEW軟件設計上位機數據采集系統的軟件部分,硬件部分由PXI數據采集卡、傳感器和計算機組成。
試驗分別以UDDS和EUDC循環工況進行驗證。測得速度、系統效率和電池SOC的曲線圖,并與仿真結果進行對比,結果如圖14所示。可以看出,臺架試驗與仿真結果趨勢基本一致。
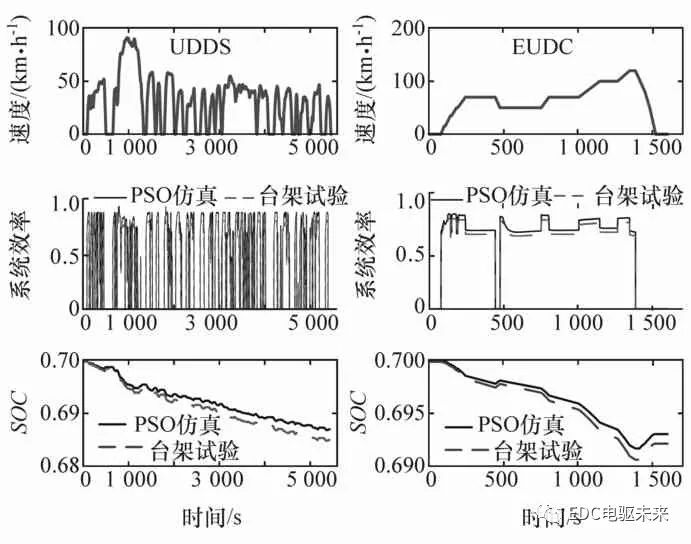
圖14 UDDS和EUDC工況下的臺架試驗與仿真結果對比
綜合上述的仿真和臺架試驗驗證的結果,表明所制定的基于PSO系統效率優化后的DMCP-EV驅動模式控制能夠有效改善雙電機驅動系統的驅動效率,從而降低了能耗,提升了整車經濟性。
4 結論
(1)針對一款新型雙電機耦合驅動系統及其多模式驅動特性,建立雙電機驅動系統動力學和系統效率模型,并制定了經PSO系統效率優化的驅動模式控制策略。
(2)通過仿真和臺架試驗驗證的結果表明,針對DMCP-EV所制定的經PSO系統效率優化的驅動模式控制策略,可獲得更合適的驅動模式,提升雙電機驅動系統的驅動效率,從而進一步提高DMCP-EV的經濟性,優化后能耗降低11%。
審核編輯:湯梓紅
-
電動汽車
+關注
關注
156文章
12110瀏覽量
231528 -
電機
+關注
關注
142文章
9031瀏覽量
145699 -
電機控制器
+關注
關注
20文章
525瀏覽量
32082 -
動力系統
+關注
關注
1文章
293瀏覽量
20668 -
雙電機
+關注
關注
0文章
14瀏覽量
4719
原文標題:雙電機耦合驅動電動汽車驅動模式劃分與優化
文章出處:【微信號:EDC電驅未來,微信公眾號:EDC電驅未來】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 雙電機耦合驅動電動汽車驅動模式劃分與優化
雙電機耦合驅動電動汽車驅動模式劃分與優化











評論