示例5–估計(jì)建筑物的高度
假設(shè)我們要用非常不精確的高度測(cè)量?jī)x來估計(jì)建筑物的高度,我們知道,建筑高度不會(huì)隨時(shí)間變化,至少在短期測(cè)量過程中是如此。
數(shù)值示例
建筑真實(shí)高度是50米。高度測(cè)量?jī)x測(cè)量誤差(標(biāo)準(zhǔn)偏差)為5米。十個(gè)測(cè)量值分別為:48.54m、47.11m、55.01m、55.15m、49.89m、40.85m、46.72m、50.05m、51.27m、49.95m。迭代0初始化可以通過簡(jiǎn)單的觀察來估計(jì)建筑物的高度,預(yù)計(jì)建筑高度為:
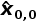
=60m
現(xiàn)在我們將初始化估計(jì)不確定度,一個(gè)人的估計(jì)誤差(標(biāo)準(zhǔn)差)約為15米:σ=15,因此,方差為225:σ2=225。
p0,0=225
預(yù)測(cè)現(xiàn)在,我們將根據(jù)初始化值預(yù)測(cè)下一個(gè)狀態(tài):由于我們系統(tǒng)是恒定的,即建筑物不會(huì)改變其高度:
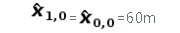
推導(dǎo)出來的估計(jì)不確定性(方差)也沒有變化:
p1,0=p0,0=225
迭代1步驟1-測(cè)量第一次測(cè)量為:z1=48.54m由于高度計(jì)測(cè)量誤差的標(biāo)準(zhǔn)偏差(σ)為5,方差(σ2)為25,因此測(cè)量不確定度為:r1=25。步驟2-更新計(jì)算卡爾曼增益:
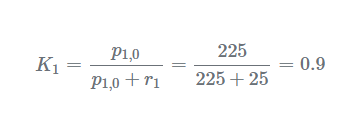
估計(jì)當(dāng)前狀態(tài):
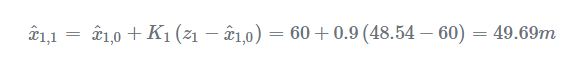
更新當(dāng)前估計(jì)的不確定度:
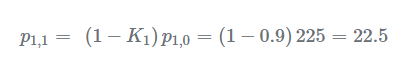
步驟3-預(yù)測(cè)由于我們系統(tǒng)是恒定的,即建筑物不會(huì)改變其高度:
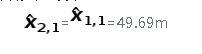
推導(dǎo)估計(jì)不確定度(方差)也沒有變化:
p2,1=p1,1=22.5
迭代2經(jīng)過一個(gè)迭代后,來自上一次迭代的預(yù)測(cè)估計(jì)變?yōu)楫?dāng)前迭代中的上一次估計(jì):
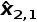
=49.69m
推導(dǎo)的估計(jì)不確定度變?yōu)橄惹暗墓烙?jì)不確定度:
p2,1=22.5
步驟1-測(cè)量第二次測(cè)量為:z2=47.11m測(cè)量不確定度為:r2=25步驟2-更新計(jì)算卡爾曼增益:
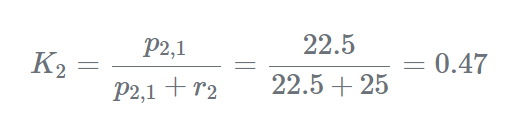
估計(jì)當(dāng)前狀態(tài):
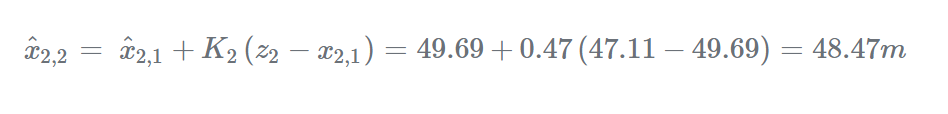
更新當(dāng)前估計(jì)的不確定度:
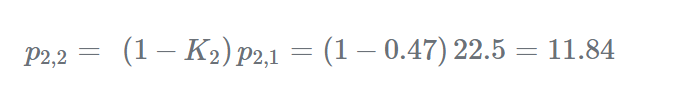
步驟3-預(yù)測(cè)由于我們系統(tǒng)是恒定的,即建筑物不會(huì)改變其高度:
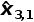
=
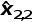
=48.47m
推導(dǎo)估計(jì)不確定度(方差)也沒有變化:
p3,2=p2,2=11.84
迭代3-10下表總結(jié)了后續(xù)迭代的計(jì)算:
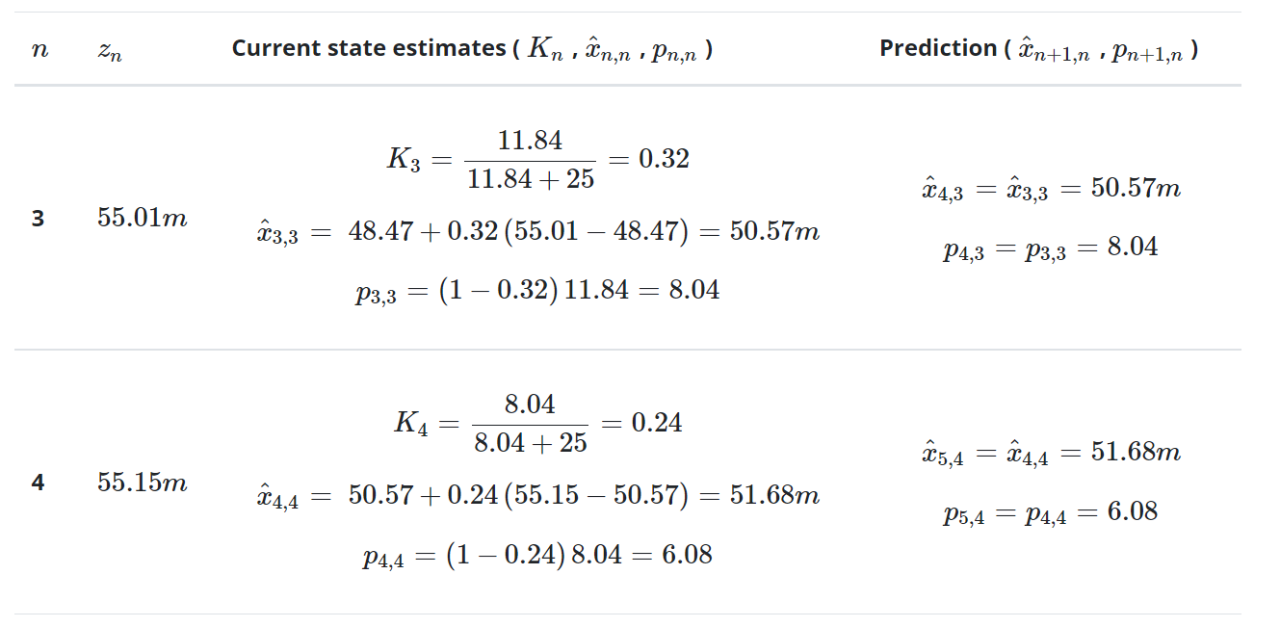
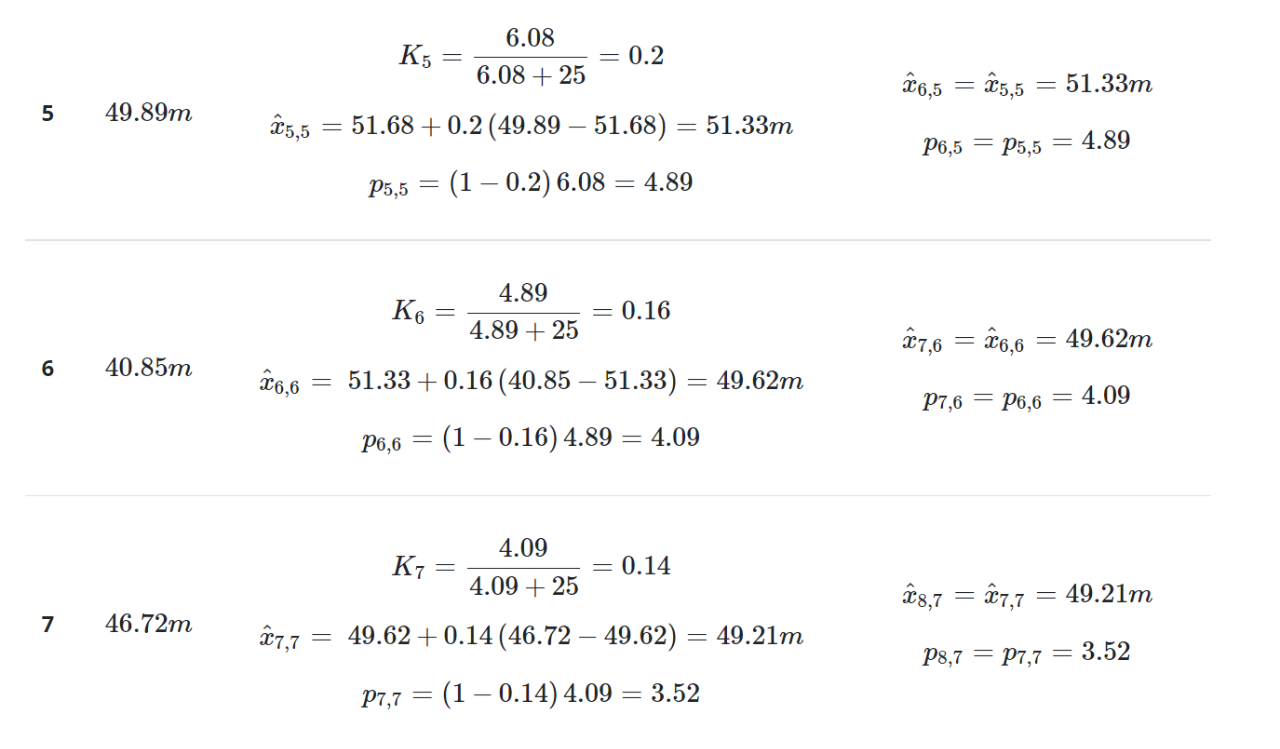
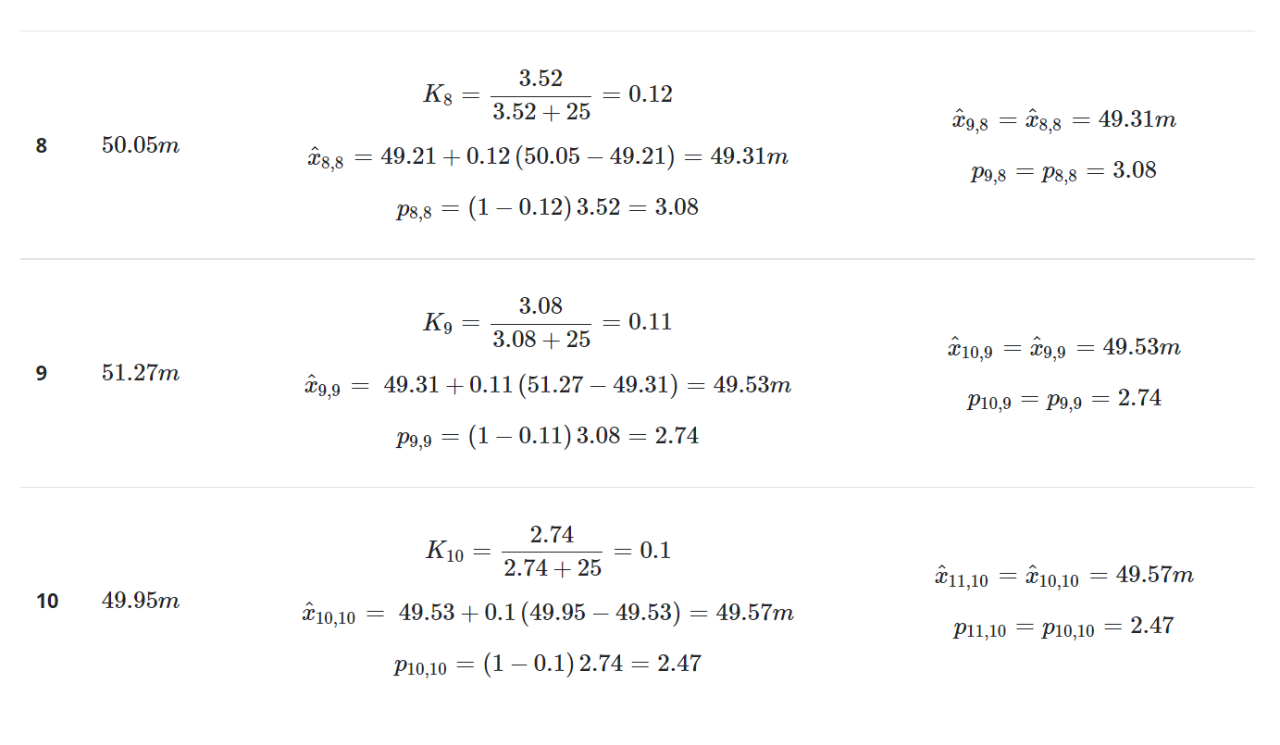
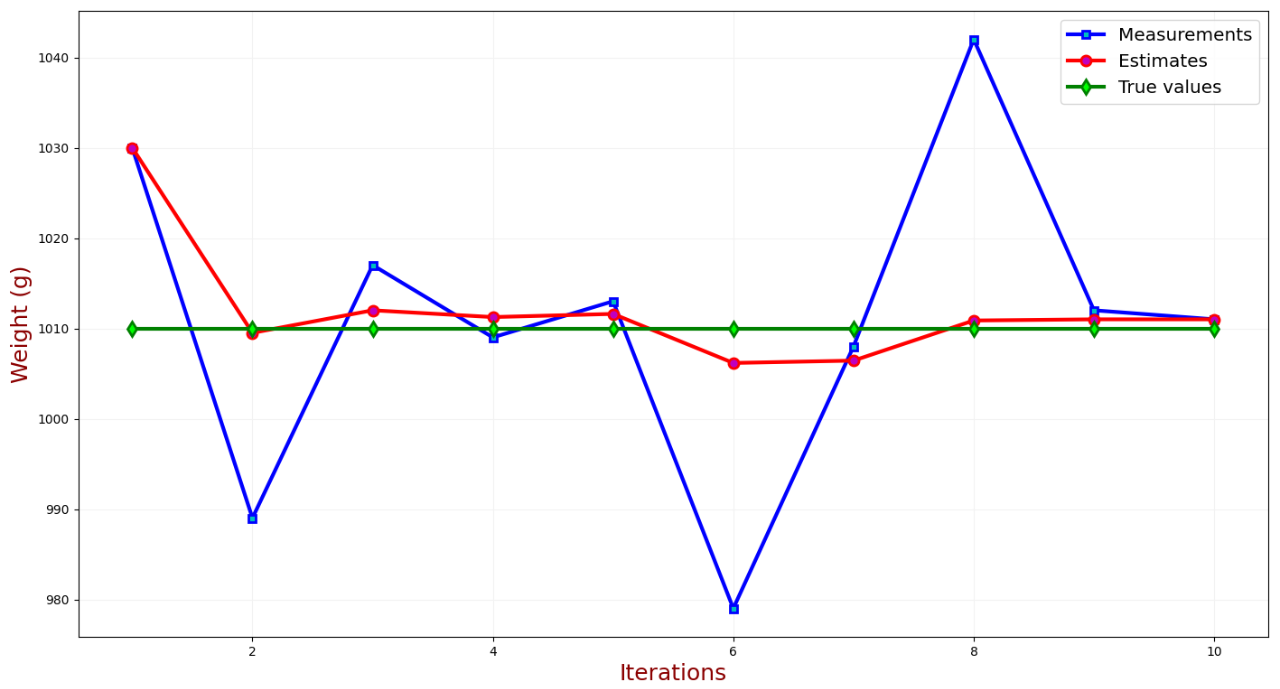
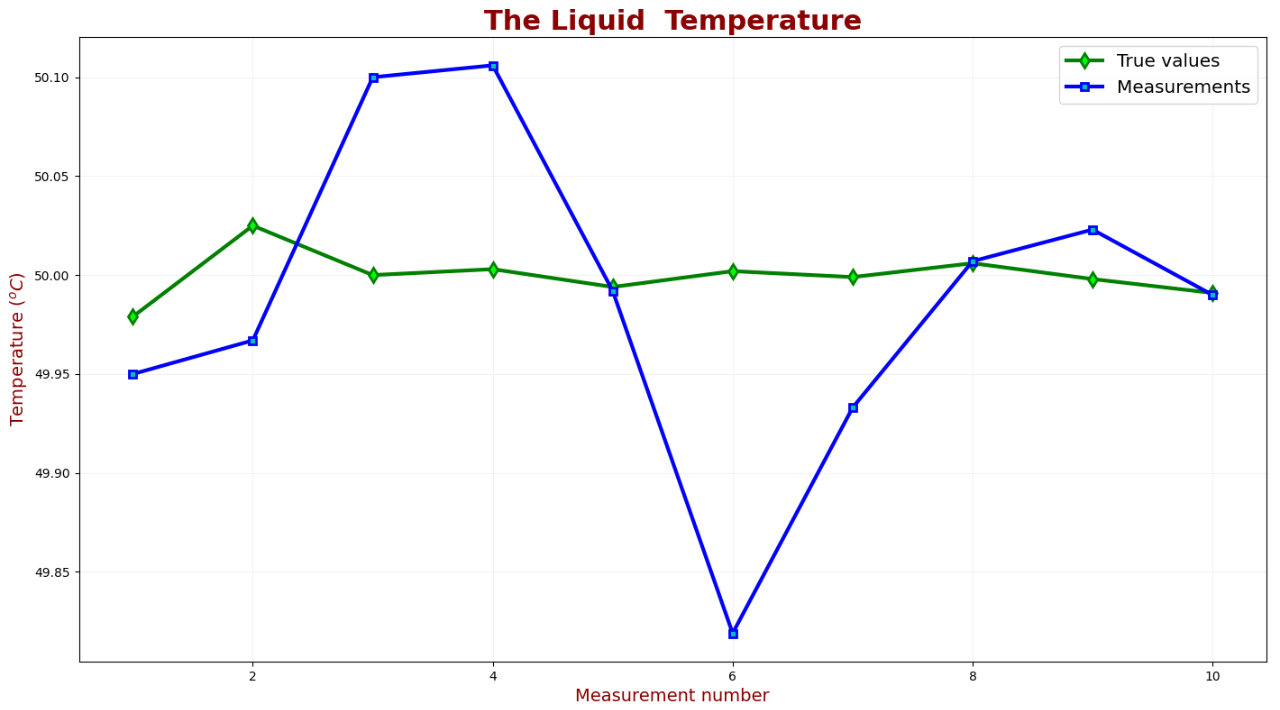
下表對(duì)真實(shí)值、測(cè)量值和估計(jì)值進(jìn)行了比較:
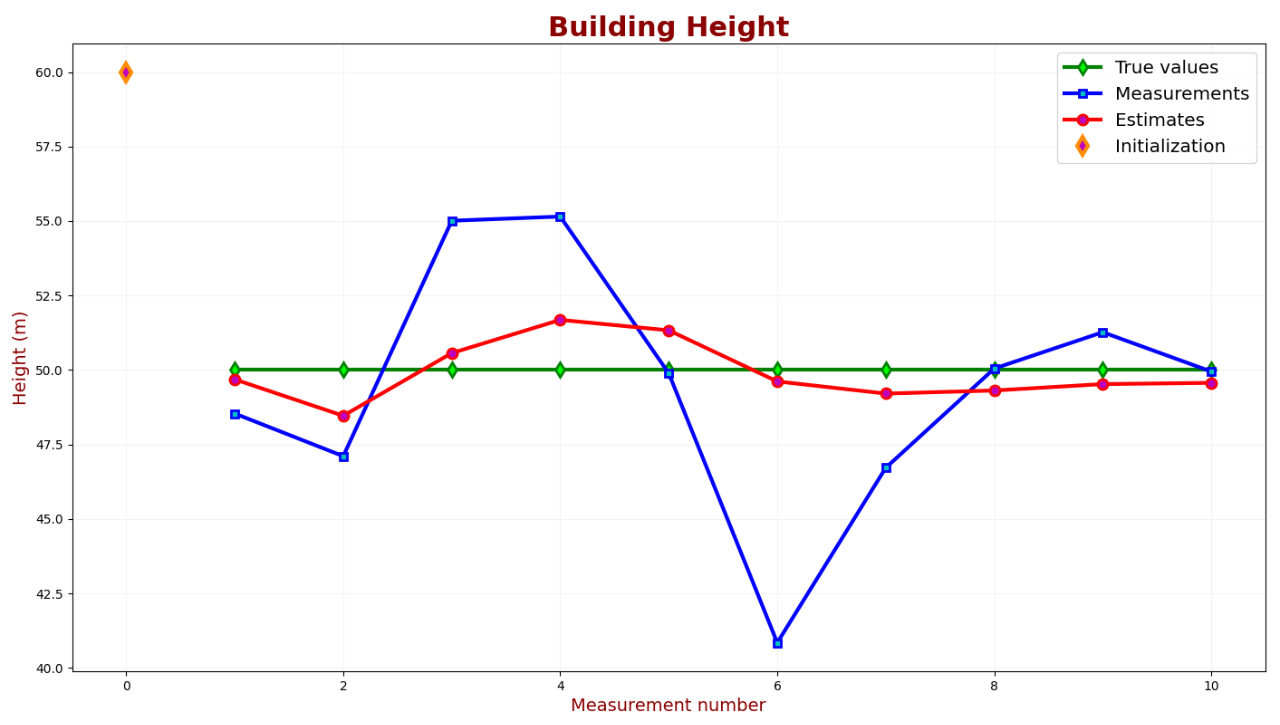
如圖可見,經(jīng)過7次測(cè)量,估計(jì)值收斂到約49.5米。下表對(duì)測(cè)量不確定度和估計(jì)不確定度進(jìn)行了比較:
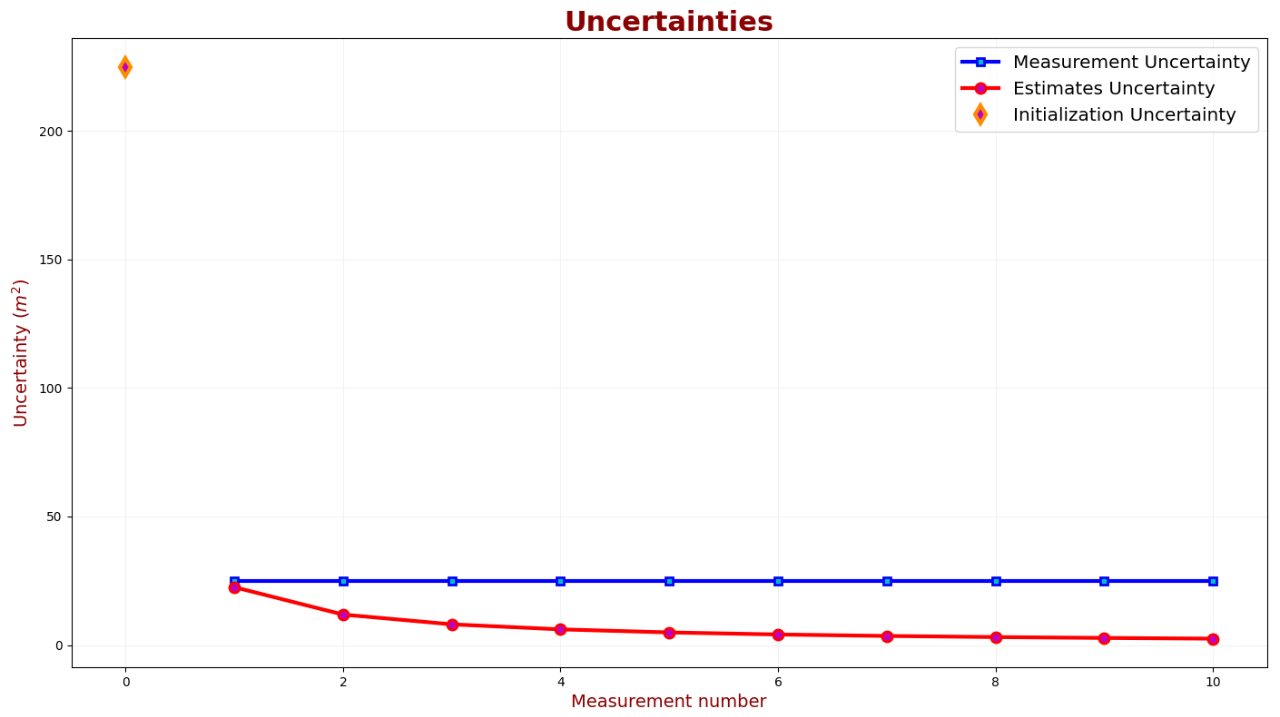
在濾波器第一輪迭代時(shí),估計(jì)不確定度接近測(cè)量不確定度,并迅速降低,10次測(cè)量后,估計(jì)不確定度(σ2)為2.47,即估計(jì)誤差標(biāo)準(zhǔn)偏差為:σ=1.57米。因此,我們可以說建筑高度估計(jì)為:49.57±1.57m。下圖顯示了卡爾曼增益:
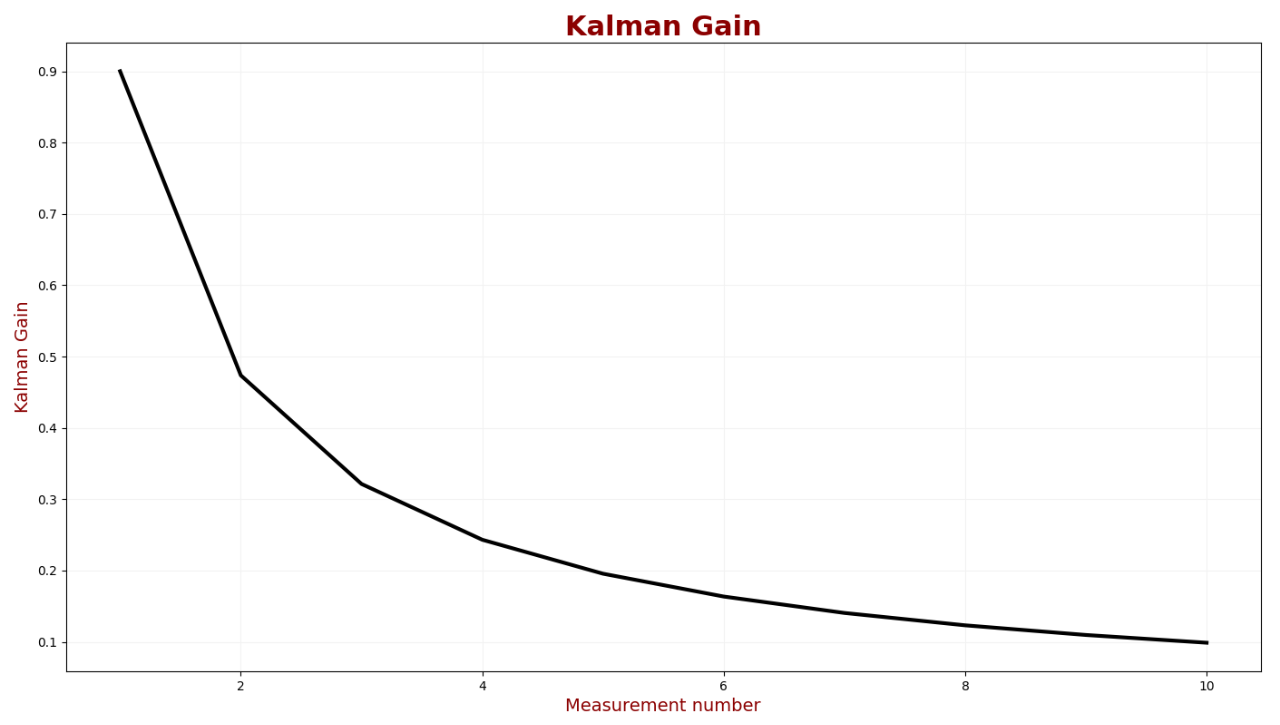
如圖所見,卡爾曼增益正在逐漸減小,使測(cè)量權(quán)重越來越小。
總結(jié):
在本例中,我們使用一維卡爾曼濾波器測(cè)量了建筑物高度,與α?β?γ不同,本示例中的卡曼增益是動(dòng)態(tài)的,取決于測(cè)量設(shè)備的精度。卡爾曼濾波器使用的初始值不是很精確,因此,狀態(tài)更新方程中的測(cè)量權(quán)重比較高,估計(jì)不確定度也很高,在后續(xù)每次迭代中,測(cè)量權(quán)重較低;因此,估計(jì)的不確定度也較低。卡爾曼濾波器輸出包括估計(jì)和估計(jì)不確定度。
一維卡爾曼濾波器的完整模型
為了使得一維卡爾曼濾波器模型更加完整,我們需要在協(xié)方差推導(dǎo)方程中添加過程噪聲變量。
過程噪聲:
在現(xiàn)實(shí)世界中,動(dòng)態(tài)系統(tǒng)模型存在不確定性,例如,當(dāng)我們想要估計(jì)電阻器的電阻值時(shí),我們假設(shè)一個(gè)恒定的動(dòng)態(tài)模型,即電阻在測(cè)量之間不改變。然而,由于環(huán)境溫度的波動(dòng),電阻可能略有變化,當(dāng)用雷達(dá)跟蹤彈道導(dǎo)彈時(shí),動(dòng)態(tài)模型的不確定性包括目標(biāo)加速度的隨機(jī)變化,由于可能的飛機(jī)機(jī)動(dòng),不確定性對(duì)飛機(jī)來說更為重要。相反,當(dāng)我們使用GPS接收機(jī)估計(jì)靜態(tài)對(duì)象的位置時(shí),由于靜態(tài)對(duì)象不移動(dòng),動(dòng)態(tài)模型的不確定性為零;動(dòng)態(tài)模型的不確定性稱為過程噪聲,在文獻(xiàn)中,它也被稱為對(duì)象干擾、驅(qū)動(dòng)噪聲、動(dòng)力學(xué)噪聲、模型噪聲和系統(tǒng)噪聲。過程噪聲產(chǎn)生估計(jì)誤差。在前面的示例中,我們估計(jì)了建筑物的高度。由于建筑物的高度沒有變化,我們沒有考慮過程噪聲。過程噪聲方差用字母q表示。協(xié)方差推導(dǎo)方程應(yīng)包括過程噪聲。對(duì)于恒定動(dòng)態(tài)系統(tǒng)模型的協(xié)方差推導(dǎo)方程為:
pn+1,n=pn,n+qn
以下是更新后的一維卡爾曼濾波方程:
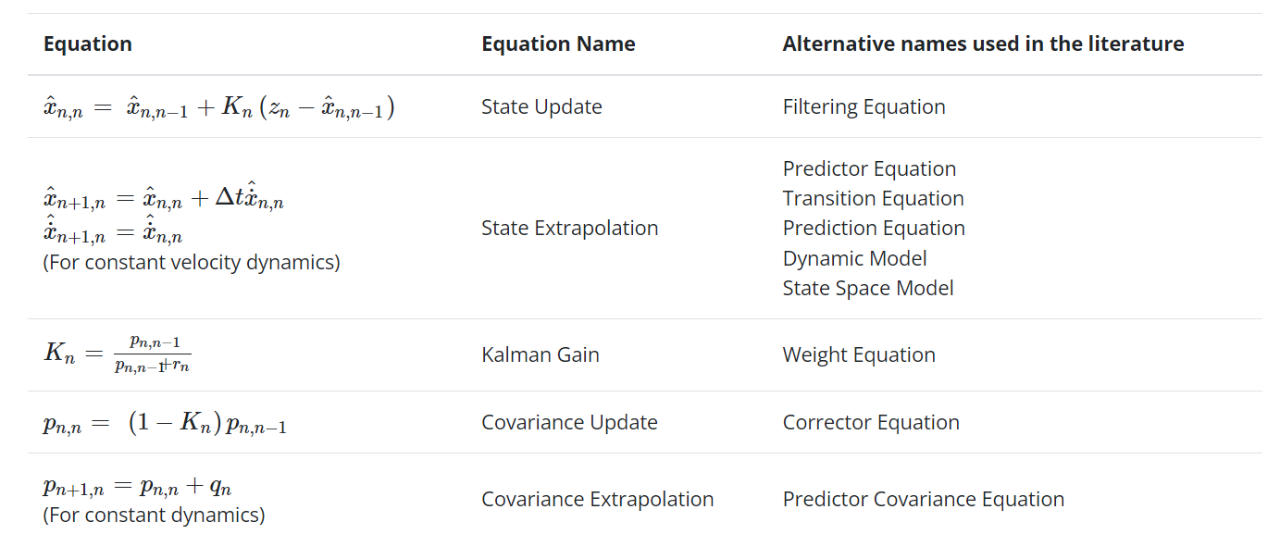
注意1:狀態(tài)推導(dǎo)方程和協(xié)方差推導(dǎo)方程取決于系統(tǒng)類型。注意2: 上表展示了針對(duì)特定情況定制的卡爾曼濾波器方程的特殊形式,方程的一般形式將在后面的矩陣表示法中給出,現(xiàn)在,我們的目標(biāo)是理解卡爾曼濾波器的概念。
-
卡爾曼濾波器
+關(guān)注
關(guān)注
0文章
54瀏覽量
12304
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
卡爾曼濾波器的使用原理
卡爾曼濾波器是什么
卡爾曼濾波器原理
卡爾曼濾波器參數(shù)分析與應(yīng)用方法研究
圖解卡爾曼濾波器

卡曼濾波器入門教程概述
卡曼濾波器入門教程α?β?γ濾波器 1
卡曼濾波器入門教程α?β?γ濾波器 2
卡曼濾波器入門教程α?β?γ濾波器 3
卡曼濾波器入門教程α?β?γ濾波器 4



















評(píng)論