本系列文章會先簡單介紹主成分分析（PCA）的基本原理，然后用實例介紹分析的過程以及算法代碼。PCA主要用于數據降維。由一系列特征組成的多維向量，其中某些元素本身沒有區分性，比如某個元素在所有的樣本中都相等，或者彼此差距不大，那么這個元素本身就沒有區分性，如果用它做特征來區分，貢獻會非常小。我們的目的是找到那些變化大的元素，即方差大的維，而去除掉那些變化不大的維。使用PCA的好處在于可以對新求出的“主元”向量的重要性進行排序。根據需要取前面最重要的部分，將后面的維數省去，從而達到降維、簡化模型或對數據進行壓縮的效果。同時最大程度地保持了原有數據的信息，較低的維數意味著運算量的減少，在數據較多的情況帶來的性能提高更明顯。

PCA通過將主成分分析的問題轉化為求解協方差矩陣的特征值和特征向量來計算。其目標是尋找r（r小于原先的個數n）個新變量，使它們反映事物的主要特征，壓縮原有數據矩陣的規模，每個新變量是原有變量的線性組合，體現原有變量的綜合效果，這r個新變量稱為“主成分”，它們可以在很大程度上反映原來n個變量的影響，并且這些新變量是互不相關的，也是正交的。主成分分析是把原來多個變量劃為少數幾個綜合指標的一種統計分析方法，從數學角度來看，這是一種降維處理技術。可以使用自帶函數來完成，也可以使用自編函數來實現！這些內容都在本文中得到體現！

PCA自帶函數！！！

MATLAB 2021a版本里面有主成分分析的函數pca。先看語法，然后在程序中使用看看效果！預先提示：計算相關系數的方式有些特別，居然用到了SVD算法，新奇！

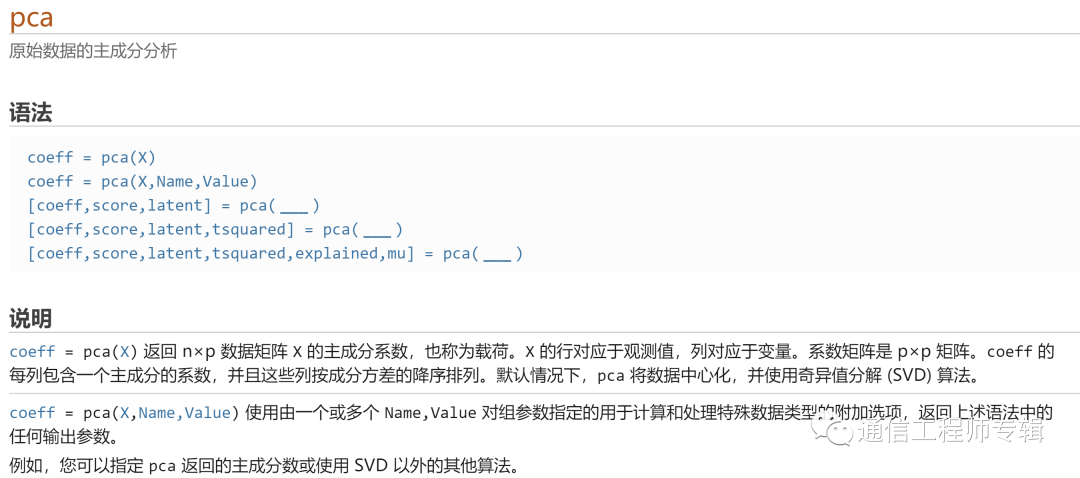
由于主成分分析（principile component analysis，PCA）這個概念在不同領域（統計學、數學等）的解釋差異較大，所以，本文通過示例使用對該函數做一點兒解釋。

語法：

coeff =pca(X)

coeff =pca(X,Name,Value)

[coeff,score,latent] =pca(___)

[coeff,score,latent,tsquared] =pca(___)

[coeff,score,latent,tsquared,explained,mu] =pca(___)

[coeff,score,latent] =pca(___)還在score中返回主成分分數，在latent中返回主成分方差。您可以使用上述語法中的任何輸入參數。主成分分數是X在主成分空間中的表示。score的行對應于觀測值，列對應于成分。主成分方差是X的協方差矩陣的特征值。

原文標題：大學課程 數據分析 實戰之主成分分析（1）

文章出處：【微信公眾號：通信工程師專輯】歡迎添加關注！文章轉載請注明出處。