Ian Beavers
這些過濾器選項中的每一個在 IMU 中都提供了截然不同的功能。在大多數情況下,它們在操作中是獨立的。它們的使用將取決于終端系統的要求。讓我們進一步了解一下細節以及它們如何應用于傳感器系統。
將抽取與有限脈沖響應(FIR)濾波器結合使用是一種降低IMU全輸入帶寬的方法,以便僅關注狹窄的低通活動頻帶。當系統受到許多旋轉和加速度頻率運動時,這尤其有用,其中只有一部分在傳感器內需要觀察。此外,任何不必要或被忽略的高頻活動都有可能混疊回目標頻帶,而不會受到FIR帶通濾波器的濾波抑制。
當不需要傳感器的全部帶寬時,FIR濾波器最有價值。相反,如果對低通區域內的已知信號頻率帶寬感興趣,則可以濾除不需要的信號。例如,系統的目標旋轉頻率可能僅在 20 Hz 到 50 Hz 之間。雖然可能還有其他更高頻率的噪聲可以檢測到,但在IMU內進行測量并不重要。圖1顯示了使用抽取和FIR濾波器選項B將全帶寬進行低通濾波16倍的方法。
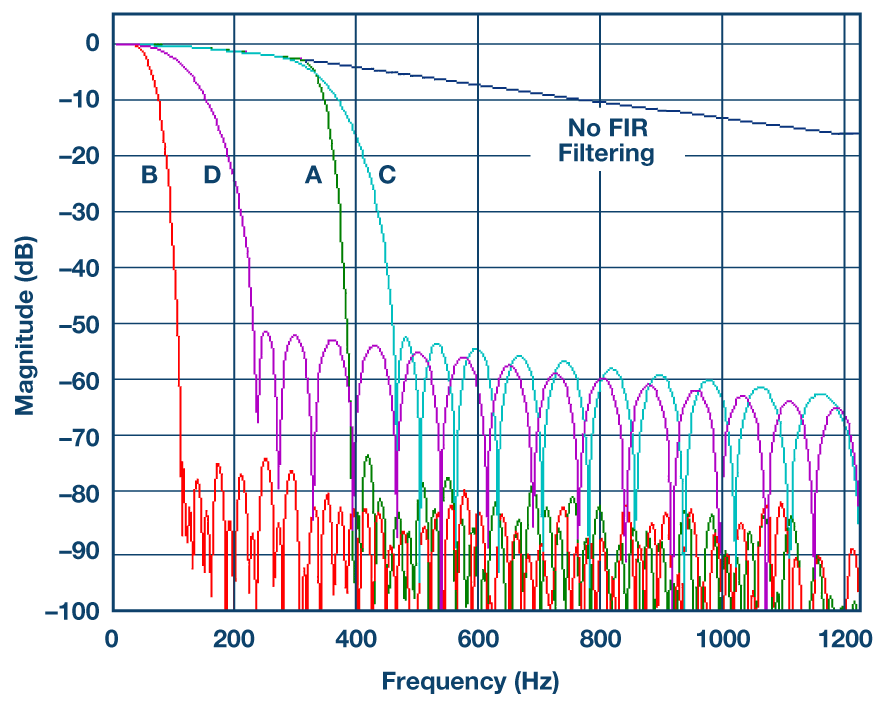
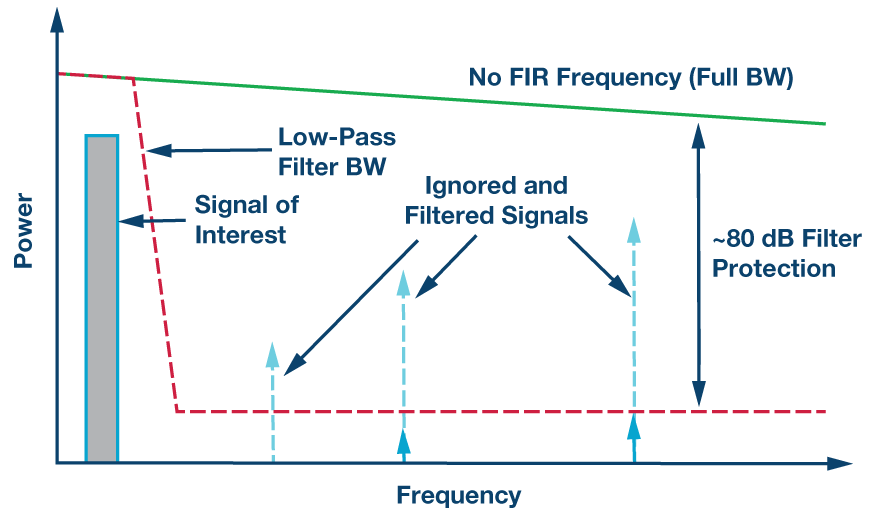
圖1.ADIS16480的FIR濾波器響應(左)和B濾波器的示例用例(右),其中可以濾除不需要的信號以聚焦在目標的低通頻率帶寬內。
卡爾曼濾波器以電氣工程師共同發明人魯道夫·卡爾曼的名字命名,與抽取濾波器和FIR濾波器組合相比,具有不同的優勢。描述卡爾曼濾波器的“濾波器”一詞實際上可能有點用詞不當。它更類似于“遞歸估計器”。卡爾曼濾波器在系統中最有價值,在這些系統中,預測位置可能比可能具有位置誤差的未濾波噪聲解更有用。卡爾曼濾波器使用 IMU 內的所有傳感器軸貢獻來估計方向角。
雖然比單個方程復雜得多,但我們可以通過刪除狀態矩陣來簡化這里的用例,我們可以得到如下所示的數學:
Xk= Kk×Zk+ (1 – Kk) × XK–1
Xk= 電流估計
Kk= 卡爾曼增益
Zk= 測量值
XK–1= 先前的估計
我們可以對待每一個k作為識別每個傳感器軸輸出的離散時間間隔或樣本。新的最佳估計是從之前的最佳估計值做出的預測,加上已知外部影響的增益校正權重。初始卡爾曼增益或協方差系數在IMU寄存器設置中使用,以建立Isensor輸出矢量之間的預期相關性。在 IMU 中使用的最佳協方差值通常取決于特定的觀測值。因此,它可以是測量、觀察數據、分析、調整和重復的迭代過程。ADIS16480采用內部算法,使用創新殘差,可以實時自適應地調整協方差項。
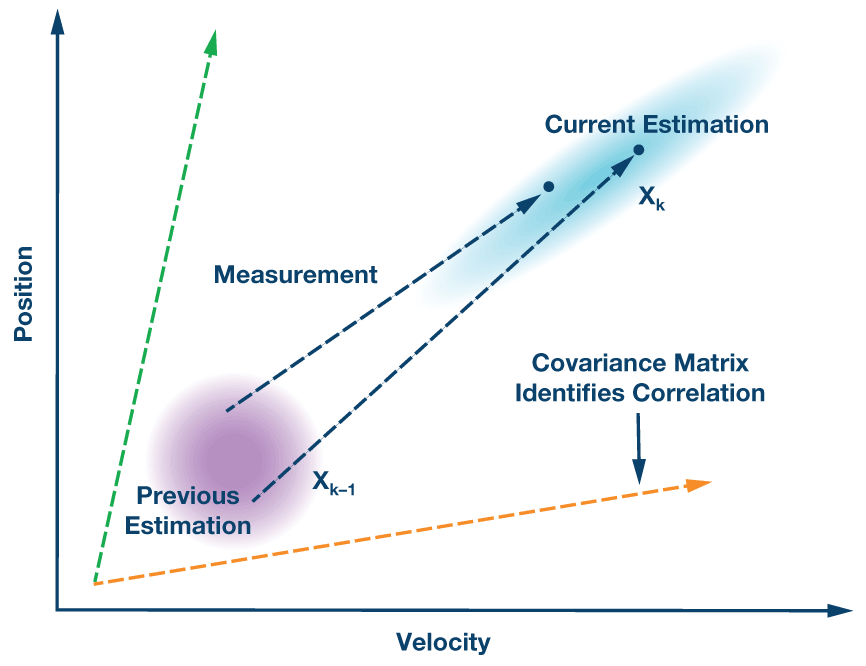
圖2.一個示例卡爾曼濾波模型,其中兩個變量(在本例中為速度和位置)具有一定程度的相關性。當前位置可以根據前一個位置、IMU 測量的加速度值以及兩者之間相關性的協方差權重來估計。
審核編輯:郭婷
-
傳感器
+關注
關注
2551文章
51162瀏覽量
754104 -
濾波器
+關注
關注
161文章
7833瀏覽量
178240 -
FIR
+關注
關注
4文章
146瀏覽量
33196
發布評論請先 登錄
相關推薦
卡爾曼濾波器是什么
如何理解卡爾曼濾波器?卡爾曼濾波器狀態方程及測量方程
卡爾曼濾波器介紹與理論分析(下)
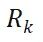
卡爾曼濾波(KF)與擴展卡爾曼(EKF)
卡爾曼濾波器的特性及仿真





 卡爾曼或FIR濾波器適用于我的IMU
卡爾曼或FIR濾波器適用于我的IMU

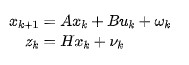











評論