使用史密斯圖進行射頻阻抗匹配的教程。示例顯示了繪制反射系數、阻抗和導納的示例。MAX2472的樣本匹配網絡采用圖形方法設計為900MHz。

經過驗證，史密斯圖仍然是確定傳輸線阻抗的基本工具。

在處理RF應用的實際實現時，總有一些噩夢般的任務。一是需要匹配互連塊的不同阻抗。通常包括天線到低噪聲放大器 （LNA）、功率放大器輸出 （RFOUT） 到天線以及 LNA/VCO 輸出到混頻器輸入。匹配任務是將信號和能量從“源”正確傳輸到“負載”所必需的。

在高射頻下，雜散元件（如導線電感、層間電容和導體電阻）對匹配網絡具有重大但不可預測的影響。在幾十兆赫茲以上，理論計算和模擬往往是不夠的。在確定適當的最終值時，必須考慮原位射頻實驗室測量以及調諧工作。需要計算值來設置結構類型和目標組件值。

有許多方法可以進行阻抗匹配，包括：

計算機模擬：復雜但易于使用，因為此類模擬器專用于不同的設計功能，而不是阻抗匹配。設計人員必須熟悉需要輸入的多個數據輸入和正確的格式。他們還需要專業知識，以便在大量結果中找到有用的數據。此外，電路仿真軟件不會預先安裝在計算機上，除非它們專用于此類應用程序。

手動計算：由于方程的長度（“公里”）和要操作的數字的復雜性，因此很乏味。

本能：只有在一個人在射頻行業投入多年后才能獲得。簡而言之，這是給超級專家的。

史密斯圖： 本文集中討論的內容。

本文的主要目的是回顧史密斯圖的結構和背景，并總結其使用的實際方法。討論的主題包括參數的實際說明，例如查找匹配的網絡組件值。當然，匹配最大功率傳輸并不是我們唯一可以用史密斯圖做的事情。它們還可以幫助設計人員完成優化最佳噪聲系數、確保品質因素影響和評估穩定性分析等任務。

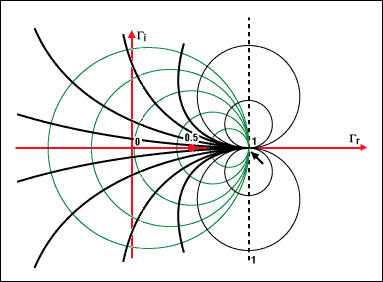
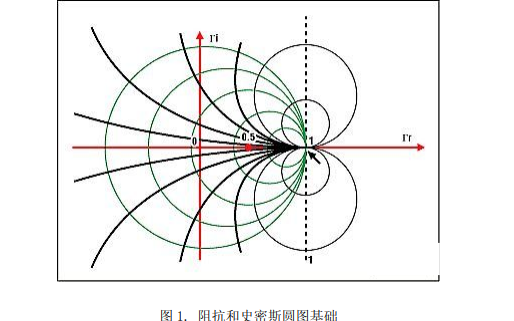
圖1.阻抗和史密斯圖的基本原理。

快速入門

在介紹史密斯圖實用程序之前，謹慎的做法是簡要回顧一下RF條件下（100MHz以上）IC布線的波傳播現象。這對于意外情況可能有效，例如RS-485線路、PA和天線之間、LNA和下變頻器/混頻器之間等。

眾所周知，為了獲得從電源到負載的最大功率傳輸，源阻抗必須等于負載阻抗的復共軛，或者：

RS+ jXS= RL- jXL

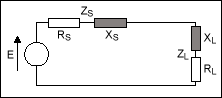
圖2.R 的示意圖S+ jXS= RL- jXL.

在這種情況下，從電源到負載的能量最大化。此外，為了進行有效的電力傳輸，需要此條件以避免能量從負載反射回電源。對于視頻線、射頻和微波網絡等高頻環境尤其如此。

它是什么

史密斯圖是一個圓形圖，上面有很多交錯的圓圈。如果使用得當，無需任何計算即可匹配具有明顯復雜結構的阻抗。唯一需要的努力是沿圓圈讀取和跟蹤值。

史密斯圖是復反射系數（也稱為伽馬，用Γ符號化）的極坐標圖。或者，它在數學上定義為 1 端口散射參數 s 或 s11.

史密斯圖是通過檢查阻抗必須匹配的負載來開發的。您不是直接考慮其阻抗，而是表示其反射系數ΓL，用于表征負載（如導納、增益和跨導）。The ΓL在處理射頻頻率時更有用。

我們知道反射系數定義為反射電壓波和入射電壓波之間的比率：

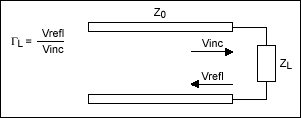
圖3.負載阻抗。

來自負載的反射信號量取決于源阻抗和負載阻抗之間的不匹配程度。其表達式定義如下：

因為阻抗是復數，所以反射系數也是一個復數。

為了減少未知參數的數量，凍結應用程序中經常出現且常見的參數很有用。這里 Z0（特性阻抗）通常是一個常數和實際的工業歸一化值，例如50Ω、75Ω、100Ω和600Ω。然后，我們可以通過以下方式定義歸一化負載阻抗：

通過這種簡化，我們可以將反射系數公式重寫為：

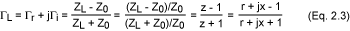
在這里，我們可以看到負載阻抗與其反射系數之間的直接關系。不幸的是，關系的復雜性在實際中沒有用，因此我們可以將史密斯圖用作上述方程的一種圖形表示。

要構建圖表，必須重寫方程以提取標準幾何圖形（如圓或雜散線）。

首先，將等式 2.3 反轉，得到：

和

通過將等式 2.5 的實部和虛部相等，我們得到了兩個獨立的新關系：

然后，通過將方程2.6至2.8發展為最終方程2.13來操縱等式2.14。該方程是以坐標 [r/（r + 1）， 0] 為中心且半徑為 1/（1 + r） 的圓的復平面 （Γr， Γi） 中的參數方程 （x - a）2 + （y - b）2 = R2 形式的關系。

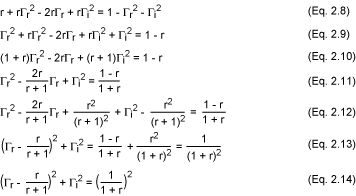
有關更多詳細信息，請參見圖 4a。

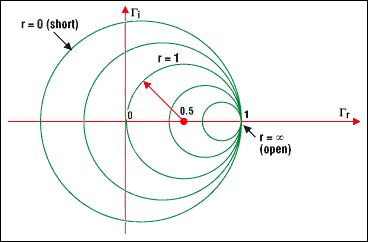
圖 4a.位于圓上的點是所有阻抗，其特征是相同的實際阻抗部分值。例如，圓 r = 1 以坐標 （0.5， 0） 為中心，半徑為 0.5。它包括點（0，0），這是反射零點（負載與特性阻抗匹配）。短路作為負載，呈現一個以坐標 （0， 0） 為中心的圓，半徑為 1。對于開路負載，圓退化為單個點（以 1， 0 為中心，半徑為 0）。這對應于最大反射系數 1，此時整個入射波被完全反射。

在開發史密斯圖時，應注意某些預防措施。這些是最重要的：

所有圓在坐標 （1， 0） 處都有一個相同的唯一相交點。

沒有阻力 （r = 0） 的零Ω圓是最大的一個。

無限電阻圓在（1， 0）處減小到一個點。

不應該有負阻力。如果發生一個（或多個），我們將面臨振蕩條件的可能性。

只需選擇與新值相對應的另一個圓圈即可選擇另一個電阻值。

從頭再來

繼續，我們使用等式 2.15 到 2.18 將等式 2.7 進一步發展為另一個參數方程。這導致等式2.19。

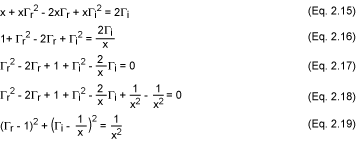
同樣，2.19 是以坐標 （1， 1/x） 為中心且半徑為 1/x 的圓的復平面 （Γr， Γi） 中類型 （x - a）2 + （y - b）2 = R2 的參數方程。

有關更多詳細信息，請參見圖 4b。

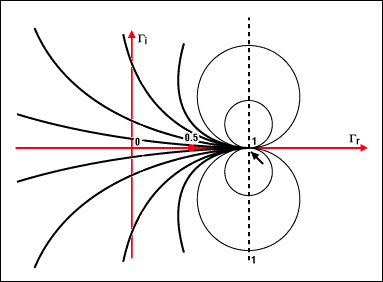
圖 4b.位于圓上的點是所有由相同的假想阻抗部分值x表征的阻抗。例如，圓 × = 1 以坐標 （1， 1） 為中心，半徑為 1。所有圓（常量 x）都包含點 （1， 0）。與實部圓不同，×可以是正數，也可以是負數。這解釋了復平面底部的重復鏡像圓。所有圓心都放置在垂直軸上，與點 1 相交。

明白了嗎？

為了完成我們的史密斯圖，我們疊加了兩個圓圈的族。然后可以看出，一個家庭的所有圓圈將與另一個家庭的所有圓圈相交。知道阻抗，以r+jx的形式，可以確定相應的反射系數。只需要找到對應于值 r 和 x 的兩個圓的交點。

這也是互惠

反向操作也是可能的。知道反射系數，找到在該點相交的兩個圓，并在圓上讀取相應的值 r 和 ×。此過程如下：

確定阻抗作為史密斯圖上的一個點。

找到阻抗的反射系數 （Γ）。

具有特性阻抗和Γ，找到阻抗。

將阻抗轉換為導納。

找到等效阻抗。

找到所需反射系數的分量值（特別是匹配網絡的元素，請參見圖 7）。

要推斷

由于史密斯圖解析技術基本上是一種圖形方法，因此解決方案的精度直接取決于圖形定義。下面是一個可以用史密斯圖表示的射頻應用示例：

例：考慮50Ω端接的特性阻抗和以下阻抗：

Z1= 100 + j50Ω	Z2= 75 - j100Ω	Z3= j200Ω	Z4= 150Ω
Z5= ∞ （開路）	Z6= 0（短路）	Z7= 50Ω	Z8= 184 - j900Ω

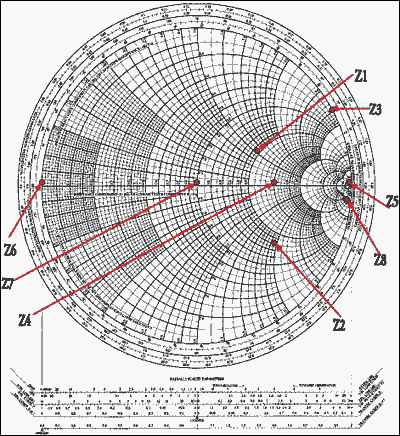
然后，歸一化并繪制圖（參見圖 5）。這些點的繪制方式如下：

z1= 2 + j	z2= 1.5 - j2	z3= j4	z4= 3
z5= 8	z6= 0	z7= 1	z8= 3.68 - j18

對于更大的圖像 （PDF）

圖5.在史密斯圖表上繪制的點。

現在可以直接提取圖5的史密斯圖上的反射系數Γ。繪制阻抗點（恒定電阻圓和恒定電抗圓的交點）后，只需讀取水平軸和垂直軸上的矩形坐標投影即可。這將得到反射系數的實部Γr和反射系數的虛部Γi（見圖6）。

也可以采用示例中介紹的八個案例，并直接從圖 6 的史密斯圖中提取其相應的Γ。這些數字是：

Γ1= 0.4 + 0.2j	Γ2= 0.51 - 0.4j	Γ3= 0.875 + 0.48j	Γ4= 0.5
Γ5= 1	Γ6= -1	Γ7= 0	Γ8= 0.96 - 0.1j

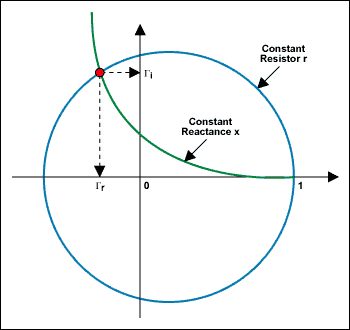
圖6.沿 X-Y 軸直接提取反射系數Γ實數和虛部。

使用準入

史密斯圖是通過考慮阻抗（電阻和電抗）來構建的。一旦建立了史密斯圖，它就可以用于分析串聯和平行世界中的這些參數。在系列中添加元素非常簡單。可以添加新元素，并通過簡單地沿著圓移動到其各自的值來確定其效果。但是，并行對元素求和是另一回事。這需要考慮其他參數。通常，在導納世界中使用并行元素更容易。

我們知道，根據定義，Y = 1/Z 和 Z = 1/Y。準入以 mhos 或 Ω 表示-1，雖然現在表示為西門子或 S。而且，由于 Z 是復雜的，因此 Y 也必須是復雜的。

因此，Y = G + jB （2.20），其中G稱為“電導”，B稱為元素的“敏感性”。不過，謹慎行事很重要。通過遵循邏輯假設，我們可以得出結論，G = 1/R 和 B = 1/X。然而，情況并非如此。如果使用此假設，則結果將不正確。

使用導納時，我們必須做的第一件事是歸一化 y = Y/Y0.這導致 y = g + jb。那么，反射系數會發生什么變化呢？通過以下工作：

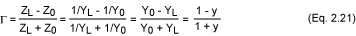
事實證明，G 的表達式與 z 相反，Γ（y） = -Γ（z）。

如果我們知道 z，我們可以反轉Γ的符號并找到一個距離 （0， 0） 相同距離但方向相反的點。通過圍繞中心點旋轉 180° 角度可以獲得相同的結果（見圖 7）。

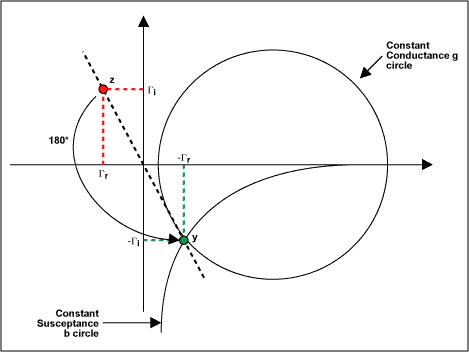
圖7.180°旋轉的結果。

當然，雖然 Z 和 1/Y 確實表示相同的分量，但新點顯示為不同的阻抗（新值在史密斯圖中具有不同的點和不同的反射值，依此類推）。發生這種情況是因為該圖是阻抗圖。但新的一點，實際上是一種承認。因此，圖表上讀取的值必須讀取為西門子。

雖然這種方法足以進行轉換，但在并行處理元件時，它不適用于確定電路分辨率。

導納史密斯圖

在前面的討論中，我們看到阻抗史密斯圖上的每個點都可以通過圍繞Γ復平面的原點旋轉 180° 來轉換為其導納對應物。因此，通過將整個阻抗史密斯控制圖旋轉180°可以獲得導納史密斯圖。這非常方便，因為它消除了構建另一個圖表的必要性。所有圓的交點（恒定電導和恒定置射）自動位于點 （-1， 0）。有了這個情節，并行添加元素也變得更加容易。在數學上，導納史密斯圖的構造由以下公式創建：

然后，反轉等式：

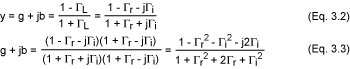
接下來，通過將等式 3.3 的實部和虛部相等，我們得到兩個新的獨立關系：

通過開發等式3.4，我們得到以下結果：

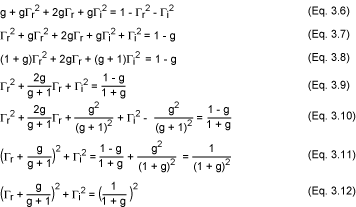
它又是圓的復平面 （Γr， Γi） 中類型 （x - a）2 + （y - b）2 = R2 （方程 3.12） 的參數方程，其坐標以 [-g/（g + 1）， 0] 為中心，半徑為 1/（1 + g）。

此外，通過開發等式3.5，我們表明：

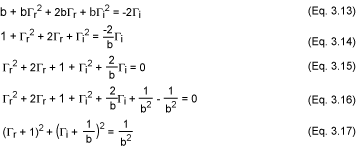
這又是類型 （x - a）2 + （y - b）2 = R2 的參數方程（方程 3.17）。

等效阻抗分辨率

在解決串聯和并聯元素混合在一起的問題時，我們可以使用相同的史密斯圖，并圍繞存在從 z 到 y 或 y 到 z 的轉換的任何點旋轉它。

讓我們考慮圖 8 的網絡（元素使用 Z 歸一化0= 50Ω).串聯電抗（x）對于電感為正，對于電容為負。磁化率（b）對電容為正，對電感為負。

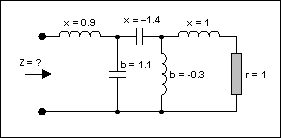
圖8.多元件電路。

電路需要簡化（見圖9）。從右側開始，那里有一個電阻器和一個值為1的電感，我們繪制一個系列點，其中r圓= 1，l圓= 1。這成為A點。由于下一個元素是分流（平行）中的元素，我們切換到導納史密斯控制圖（通過將整個平面旋轉 180°）。但是，要做到這一點，我們需要將前一點轉換為準入。這變成了 A'。然后我們將平面旋轉 180°。我們現在處于準入模式。分流元件可以通過沿電導圈移動對應于0.3的距離來添加。這必須以逆時針方向（負值）完成，并給出點 B。然后我們還有另一個系列元素。我們再次切換回阻抗史密斯圖。

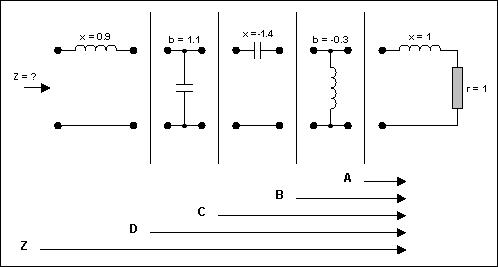
圖9.圖 8 的網絡及其元素進行了細分分析。

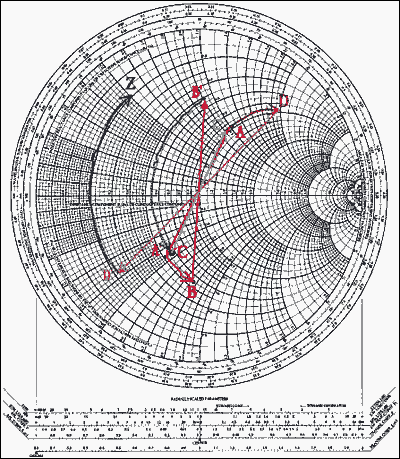
在執行此操作之前，再次有必要將前一點重新轉換為阻抗（這是導納）。轉換后，我們可以確定 B'。使用先前建立的例程，圖表再次旋轉 180° 以返回到阻抗模式。串聯元件是沿著電阻圈沿著對應于1.4的距離和標記點C相加的。這需要逆時針完成（負值）。對于下一個元素，將執行相同的操作（轉換為導納和平面旋轉）。然后沿恒定電導圈順時針方向移動規定的距離（1.1）（因為該值為正）。我們將其標記為 D。最后，我們重新轉換回阻抗模式并添加最后一個元件（串聯電感）。然后，我們確定位于電阻圓 0.2 和電抗圓 0.5 的交點處的所需值 z。因此，z 被確定為 0.2 + j0.5。如果系統特性阻抗為50Ω，則Z = 10 + j25Ω（見圖10）。

對于更大的圖像 （PDF）

圖 10.繪制在史密斯圖上的網絡元素。

按步驟匹配阻抗

史密斯圖的另一個功能是能夠確定阻抗匹配。這是查找給定網絡的等效阻抗的反向操作。此處，阻抗固定在兩個接入端（通常是源極和負載），如圖11所示。目標是設計一個在它們之間插入的網絡，以便進行適當的阻抗匹配。

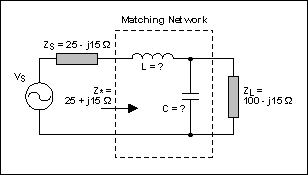
圖 11.具有已知阻抗和未知元件的代表電路。

乍一看，這似乎并不比找到等效阻抗更困難。但問題是，可以存在無限數量的匹配網絡組件組合，從而產生類似的結果。可能還需要考慮其他輸入（例如濾波器類型結構、質量因數和有限的組件選擇）。

為此選擇的方法需要在史密斯圖上添加串聯和分流元件，直到達到所需的阻抗。從圖形上看，它似乎找到了一種鏈接史密斯圖上的點的方法。同樣，說明該方法的最佳方法是以需求為例。

目標是匹配源阻抗（ZS） 到負載 （Z）L）的工作頻率為60MHz（見圖11）。網絡結構已固定為低通，L型（另一種方法是將問題視為如何強制負載顯示為值= Z的阻抗S，Z 的復共軛物S).以下是找到解決方案的方法。

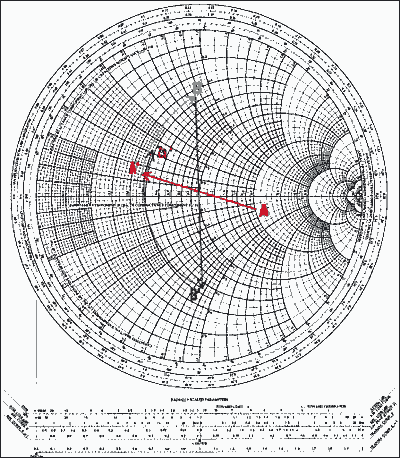
對于更大的圖像 （PDF）

圖 12.圖 11 的網絡及其點繪制在史密斯圖上。

首先要做的是規范化不同的阻抗值。如果未給出，請選擇與荷載/源值在相同范圍內的值。假設 Z0為50Ω。因此 zS= 0.5 - j0.3， z*S= 0.5 + j0.3，并且zL= 2 - j0.5。

接下來，在圖表上定位兩個點。標記 A 表示 zL和 D 表示 z*S.

然后確定連接到負載的第一個元件（并聯中的電容器）并轉換為導納。這給了我們A'點。

確定電容器C連接后下一個點將出現的電弧部分。由于我們不知道C的值，因此我們不知道在哪里停止。然而，我們確實知道方向。分流中的 C 表示在導納史密斯控制圖上沿順時針方向移動，直到找到該值。這將是B點（準入）。由于下一個元件是串聯元件，因此必須將B點轉換為阻抗平面。然后可以獲得B'點。B'點必須與D位于同一電阻圓上.圖形上，從A'到D只有一個解決方案，但中間點B（因此B'）需要通過“測試和嘗試”設置進行驗證。找到點 B 和 B' 后，我們可以測量弧 A' 到 B 和弧 B' 到 D 的長度。第一個給出 C 的歸一化置疑值。第二個給出L的歸一化電抗值。弧 A' 到 B 的測量值為 b = 0.78，因此 B = 0.78 × Y0= 0.0156S。因為ωC = B，那么C = B/ω = B/（2 π f） = 0.0156/[2π（60 × 106）] = 41.4pF。

弧 B' 到 D 的測量值為 x = 1.2，因此 X = 1.2 × Z0= 60Ω.因為 ωL = X，所以 L = X/ω = X/（2 π f） = 60/[2π（60 × 106）] = 159nH。

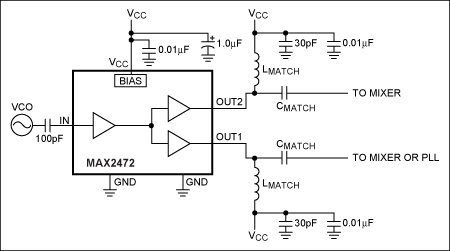
圖 13.MAX2472典型工作電路

第二個示例將MAX2472的輸出與50Ω負載阻抗（zL）的工作頻率為900MHz（見圖14）。該網絡將使用MAX2472數據資料中所示的相同配置。上圖顯示了具有并聯電感器和串聯電容器的匹配網絡。以下是找到解決方案的方法。

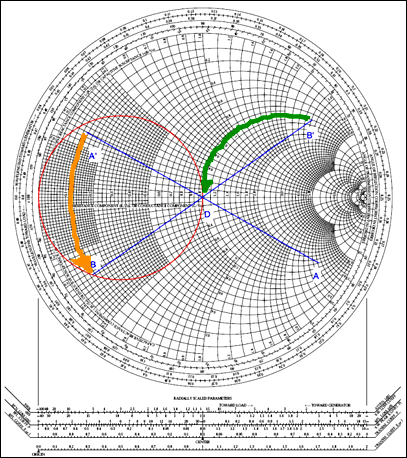
圖 14.圖 13 的網絡及其點繪制在史密斯圖上。

首先要做的是轉換 S22散射參數轉換為其等效歸一化源阻抗。MAX2472使用Z0為50Ω。因此 S22= 0.81/-29.4° 變為 zS= 1.4 - j3.2， zL= 1 和 zL* = 1。

接下來，在圖表上定位兩個點。標記 A 表示 zS和 D 表示 zL*.由于連接到源的第一個元件是并聯電感，因此請將源阻抗轉換為導納。這給了我們A'點。

確定電感L連接后下一個點將出現的電弧部分火柴.因為我們不知道L的值火柴，我們不知道在哪里停下來。但是，我們確實知道，在添加 L 之后火柴（并轉換回阻抗），得到的源阻抗應位于r = 1圓上。因此，附加串聯電容器C火柴可以使所得阻抗達到z = 1 + J0。通過將r = 1圓圍繞原點旋轉180°，我們繪制出與r = 1圓相對應的所有可能的導納值。這個反射圓和與點A'一起使用的恒定電導圓的交點給了我們B點（導納）。B點對阻抗的反射成為B'點。

找到點 B 和 B' 后，我們可以測量弧 A' 到 B 和弧 B' 到 D 的長度。第一次測量給出L的歸一化置化置化值火柴.第二個給出C的歸一化電抗值火柴.弧 A' 到 B 的測量值為 b = -0.575，因此 B = -0.575 × Y0= 0.0115S。因為 1/ωL = B，那么 L火柴= 1/Bω = 1/（B2πf） = 1/（0.01156 × 2 × π × 900 × 106） = 15.38nH，四舍五入為 15nH。弧 B' 到 D 的測量值為 × = -2.81，因此 X = -2.81 × Z0= -140.5Ω.因為 -1/ωC = X，那么C火柴= -1/Xω = -1/（X2πf） = -1/（-140.5 × 2 × π × 900 × 106） = 1.259pF，四舍五入為 1pF。雖然這些計算值未考慮元件的寄生電感和電容，但它們產生的值接近數據手冊規定的值L火柴= 12nH 和 C火柴= 1pF。

結論

鑒于當今軟件的豐富性和高速高功率計算機的可訪問性，人們可能會質疑是否需要這種基本和基本的方法來確定電路基本原理。

實際上，使工程師成為真正工程師的不僅是學術知識，還有使用各種資源解決問題的能力。將幾個數字插入程序并讓它吐出解決方案很容易。當解決方案復雜且多方面時，擁有一臺計算機來完成繁重的工作特別方便。但是，了解已移植到計算機平臺的基本理論和原理以及它們的來源，使工程師或設計師成為更全面和自信的專業人士，并使結果更加可靠。

審核編輯：郭婷