1.1 傅里葉變換

1.1.1 傅里葉變換概述

傅里葉變換是一種可以將滿足某個條件的函數(shù)表示成三角函數(shù)（正弦或余弦）表示的線性組合，最初，傅里葉分析是作為熱過程解析分析的工具被提出的，在電路中，這是一種分析非正弦周期信號的最便捷的工具，傅里葉是法國數(shù)學(xué)家和物理學(xué)家，在1807年的法國科學(xué)學(xué)會上發(fā)表了運用正弦曲線來描述溫度分布，但是論文中有一個具有爭議性的判定，即任何連續(xù)周期信號都可以由一組適當(dāng)?shù)恼仪€組合而成，當(dāng)時拉普拉斯與其他審查者投票通過并要發(fā)表這個論文，但是拉格朗日認(rèn)為傅里葉提供的方法無法表示帶有棱角的信號，由于一些原因，這篇論文直到拉格朗日去世15年后才被發(fā)表，其實拉格朗日當(dāng)時的想法是對的，正弦曲線的確無法組合一個帶有棱角的信號，但是我們可以采用正弦曲線組合成的信號來無限的逼近這個信號，直到兩種信號不存在能量差別。

通過上面的描述可以得到一個結(jié)論，傅里葉變換是一種將不規(guī)則信號通過正弦信號的線性組合表示出來的方法，但是為什么不用方波或者三角波來表示原信號呢，這是因為分解信號的方法是無窮的，但分解信號的目的是為了更加簡單地處理原來的信號。用正余弦來表示原信號會更加簡單，因為正余弦擁有原信號所不具有的性質(zhì)：正弦曲線保真度。一個正弦曲線信號輸入后，輸出的仍是正弦曲線，只有幅度和相位可能發(fā)生變化，但是頻率和波的形狀仍是一樣的。且只有正弦曲線才擁有這樣的性質(zhì)，正因如此我們才不用方波或三角波來表示。

我們從物理系統(tǒng)的特征信號角度來解釋為什么不能用其他信號的線性組合來表示原始信號，我們生活中常見的現(xiàn)象大多屬于 線性時不變系統(tǒng) （輸入信號與輸出信號滿足線性關(guān)系，且系統(tǒng)參數(shù)不隨時間變換），無論你采用微分方程或者傳遞函數(shù)還是狀態(tài)空間，所以可以說正弦信號是系統(tǒng)的特征向量，當(dāng)然指數(shù)信號也是系統(tǒng)的特征向量，用于標(biāo)識能量的衰減與累計，系統(tǒng)中的衰減或擴散現(xiàn)象大多數(shù)是指數(shù)形式或者復(fù)指數(shù)形式，但是如果輸入的是方波或者三角波，那輸出就不一定是什么形式了，所以，除了指數(shù)信號與正弦信號外其他信號都不是線性系統(tǒng)的特征信號。

1.1.2 時域與頻域

從我們出生開始，我們看到的世界都是以時間貫穿，人的身高走勢，汽車的軌跡都會隨著事件發(fā)生改變，這種以時間作為參照來觀察分析動態(tài)世界的方法就屬于時域分析，頻域則是描述信號在頻率方面特性時用到的一種坐標(biāo)系，頻域不是真實存在的，只是一種數(shù)學(xué)構(gòu)建的領(lǐng)域，是一個遵循特定規(guī)則的數(shù)學(xué)范疇，正弦信號是頻域中唯一存在的波形，即正弦信號是對頻域的描述。

1.1.3 定義

也就是說我們只需要求出上面的幾個參數(shù)的值，就可以根據(jù)定義式將函數(shù)轉(zhuǎn)化為傅里葉級數(shù)的形式。與傅里葉級數(shù)相對應(yīng)的就是傅里葉變換，這個定義式就簡單的多。

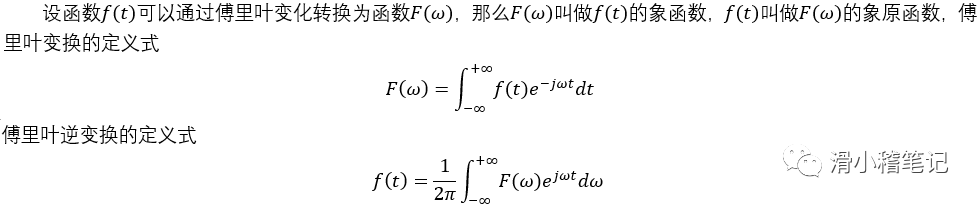
根據(jù)上面的兩個公式可以發(fā)現(xiàn)，傅里葉變換后的象函數(shù)是以頻率作為自變量的函數(shù)，而逆變換后的函數(shù)則是以時間作為自變量的函數(shù)，我們將象函數(shù)用圖像的形式表示出來就成了自變量是頻率的二維圖像，這個圖像就稱為頻譜圖。

1.2 頻域圖像

在電路分析基礎(chǔ)中，傅里葉經(jīng)常被用于分析非正弦周期信號電路中，即講一個輸入激勵構(gòu)建數(shù)學(xué)模型，采用積分的方式轉(zhuǎn)化為傅里葉級數(shù)，通過計算每個頻率狀態(tài)下的電參數(shù)最終分析電路整體的電參數(shù)，這就不僅需要最終的級數(shù)形式，還需要頻域圖像來輔助分析，在這里，我們采用MATLAB來把上面例題中的頻域圖像繪制出來，MATLAB的源代碼如下：

clc
clear
%系數(shù)計算（用于構(gòu)建傅里葉級數(shù)）
syms t n;
m = 100 ;                                                    %高次諧波疊加次數(shù)
T = 2 ;                                                      %信號的周期
f = t^2 ;                                                    %函數(shù)表達(dá)式
a0 = int( f, t, -T/2, T/2 )/T ;
an = int( f*cos(n*pi*t), t, -T/2, T/2 ) ;
bn = int( f*sin(n*pi*t), t, -T/2, T/2 ) ;
%轉(zhuǎn)換定義式的形式
n = -round(T+1):1:round(T+1);
anVal = eval( an ) ;                                       %生成an系數(shù)矩陣
bnVal = eval( bn ) ;                                       %生成bn系數(shù)矩陣
An = sqrt( anVal.^2+bnVal.^2 ) ;                         %幅值開平方計算
An( round( length(n)/2 ) ) = a0 ;
phi = atan( -bnVal./anVal ) ;                             %相位計算
phi( round( length(n)/2 ) ) = 0 ;
%繪制幅度譜
figure(1);
subplot( 2, 1, 1 ) ;
stem( n, An ) ;
title( '幅度譜' ) ;
xlabel( 'n' ) ;
ylabel( 'An' ) ;
%繪制相位譜
subplot( 2, 1, 2 ) ;
plot( n, phi ) ;
title( '相位譜' ) ;
xlabel( 'n' ) ;
ylabel( '|×n' ) ;
%高次諧波擬合函數(shù)曲線
figure( 2 ) ;
t = -T: 0.01: T ;
f = a0 ;
for n=1:m
    f = f+eval(an)*cos(n*pi.*t);
    f = f+eval(bn)*sin(n*pi.*t);
end
plot( t, f ) ;
title( strcat( num2str( n ), '次諧波疊加') ) ;
xlabel( 't' ) ;
ylabel( 'f(t)' ) ;

最終仿真的結(jié)果如下圖所示。

1.3 DFT算法的MATLAB實現(xiàn)

傅里葉變換主要分為4類：

（1）傅里葉級數(shù)：將周期性連續(xù)函數(shù)轉(zhuǎn)換為離散頻率點

（2）連續(xù)傅里葉變換：將連續(xù)函數(shù)變換為連續(xù)頻率函數(shù)

（3）離散時間傅里葉級數(shù)DFS：將離散函數(shù)變換為連續(xù)頻率的函數(shù)

（4）離散傅里葉變換DFT：將有限長離散函數(shù)變換為離散頻率點上的函數(shù)

利用MATLAB自帶的fft函數(shù)實現(xiàn)DFT運算，源代碼如下。

%45點采樣
subplot( 2, 2, 1 );
N = 45 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=45')
%50點采樣
subplot( 2, 2, 2 ) ;
N = 50 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=50')
%55點采樣
subplot( 2, 2, 3 ) ;
N = 55 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=55')
%60點采樣
subplot( 2, 2, 4 ) ;
N = 60 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=60')

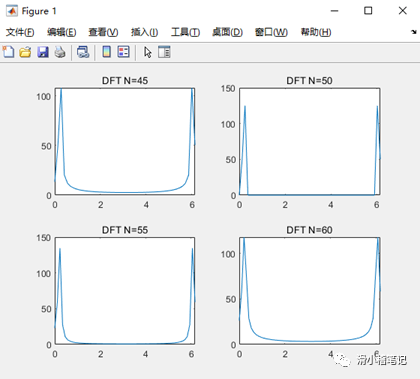
MATLAB運行截圖如下所示。

我們進(jìn)一步增加截取長度與DFT點數(shù)，例如增加到256：

N = 256 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=256')

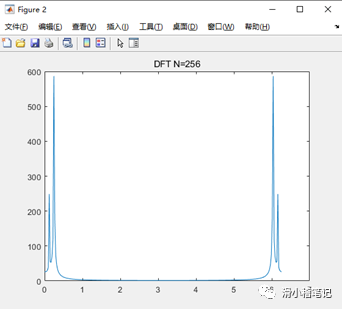
此時信號的頻譜如下圖所示。

假設(shè)采樣頻率f=100Hz，采樣間隔T=0.01s時，取樣點N的值越大，則譜分辨率F=f/N越小，說明此時分辨率越高，加入采樣點為256時，既可以實現(xiàn)兩個不同頻率信號的區(qū)分。

1.4 FFT算法的MATLAB實現(xiàn)

FFT是離散傅立葉變換DFT的快速計算方法，適用于離散信號，并且注意變換后的點數(shù)與信號的采樣點數(shù)一致，盡管可以將信號補0，但補0不能提高頻域的分辨率。matlab中提供了函數(shù)fft做一維的FFT。

（1）時域譜和頻域譜是相互對應(yīng)；時域的信號長度，決定頻域的采樣間隔，它們成導(dǎo)數(shù)關(guān)系；

（2）時域中信號有N點，每點間隔dt，所以時域信號長度為Ndt；那么頻譜每點的間隔就是1/(Ndt)。

clc
clear
N = 256 ;
dt = 0.02 ;
n = 0:N-1 ;
t = n*dt ;
x = sin(2*pi*t) ;
m = N ;
a = zeros( 1, m ) ;
b = zeros( 1, m ) ;
c = zeros( 1, m ) ;
for k=0:m-1
    for i=0:N-1
        a( k+1 )= a( k+1 )+2/N*x( i+1 )*cos( 2*pi*k*i/N ) ;
        b( k+1 )= b( k+1 )+2/N*x( i+1 )*sin( 2*pi*k*i/N ) ;
    end
c( k+1 ) = sqrt( a( k+1 )^2+b( k+1 )^2 ) ;
end
%時域圖
subplot( 2, 1, 1 ) ;
plot( t, x ) ;
title( '原始信號' ) ;
xlabel( 't' ) ;
ylabel( 'f(t)' ) ;
%頻域圖像
f = ( 0:m-1 )/( N*dt ) ;
subplot( 2, 1, 2 ) ;
plot( f, c ) ;hold on
title( 'Fourier' ) ;
xlabel( '頻率/HZ' ) ;
ylabel( '幅值' ) ;
%計算頻率
ind = find( c==max(c), 1, 'first' ) ;                                  %查找頻率第一個最大值
x0 = f( ind );                                                              %得到橫坐標(biāo)
y0 = c( ind );                                                              %得到縱坐標(biāo)
plot( x0, y0, 'ro' );hold off
text( x0+1, y0-0.1, num2str( x0, '頻率=%f' ) ) ;

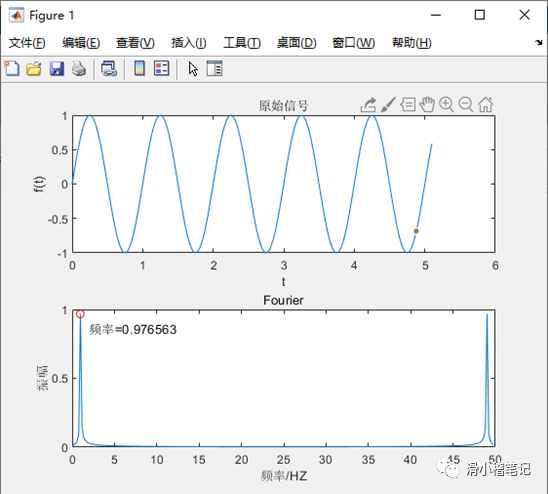
MATLAB運行結(jié)果如下圖所示。

1.3基于51單片機的頻譜設(shè)計

1.3.1 功能

我們現(xiàn)在使用51單片機來實現(xiàn)頻譜的顯示，通過輸入音頻信號來輸出對應(yīng)的頻段的幅值，這次選用的是STC12C5A60S2，運行時鐘33MHz，內(nèi)置ADC采樣，利用LED組成點陣顯示屏幕，通過ADC不停的采樣音頻數(shù)據(jù)，將數(shù)據(jù)轉(zhuǎn)換為頻域幅值顯示在LED上面。

1.3.2 原理圖分析

（1）最小系統(tǒng)電路

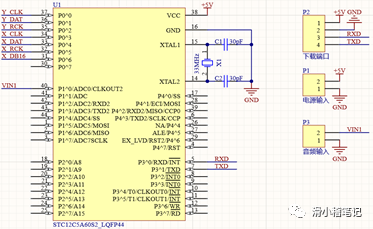
單片機系統(tǒng)采用國產(chǎn)的51單片機，在之前的51單片機中我們已經(jīng)具體了解過51單片機的應(yīng)用，這里不再詳細(xì)贅述，我們這次采用的是33MHz的晶振，STC12C系列相對于傳統(tǒng)的51單片機來說，運行速度快了接近12倍，可以運行256位的FFT算法，程序采用串口的方式燒錄進(jìn)去，其中P1口可以設(shè)置為ADC輸入口，內(nèi)置8通道10位ADC轉(zhuǎn)換器，采用直流5V供電。

（2）LED驅(qū)動電路

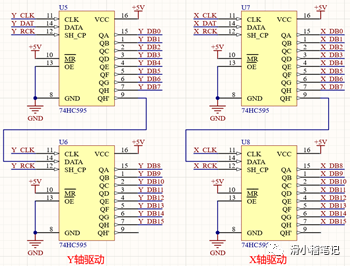
由于我們使用的單片機只有44個引腳，實際能用的IO端口僅有35個，而我們是用的是17×16的矩陣，需要33個端口，去掉1組串口，1個ADC，剩下的端口速度各不相同，已經(jīng)無法滿足驅(qū)動的需要，所以采用74HC595芯片作為驅(qū)動電路，74HC595是一個可以將串行數(shù)據(jù)轉(zhuǎn)換為并行數(shù)據(jù)的芯片，并且可以通過級聯(lián)的方式輸出數(shù)據(jù)，我們采用2片595芯片的級聯(lián)來實現(xiàn)串行數(shù)據(jù)轉(zhuǎn)16位并行的的效果，其余的1位數(shù)據(jù)通過IO口來達(dá)到控制的目的。74HC595的時序圖如下圖所示。

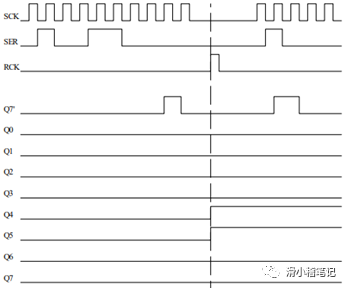
（3）點陣顯示電路

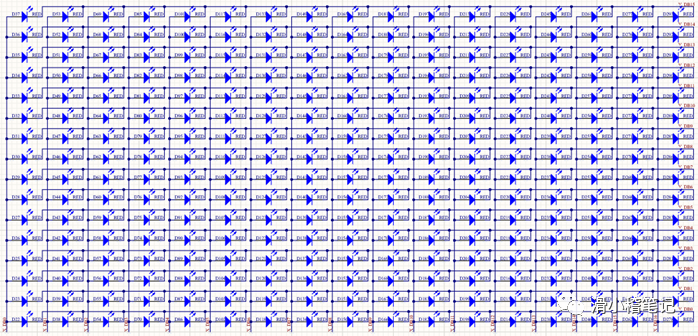
這里采用17×16的點陣作為顯示，這種點陣連接的方式可以通過控制17+16=33個端口來實現(xiàn)17*16=272個LED亮滅的控制。