今天來看一個比較復雜的排序，堆排序，先搞清楚原理，再寫代碼。

堆排序使用數據結構中的堆來完成，那么問題來了，什么是堆？

有兩種，大頂堆和小頂堆，所謂大頂堆，就是任意一個雙親節點都比孩子節點大，比如圖上這樣的，小頂堆則反過來。

所以對于大頂堆來說，根節點一定是最大的。

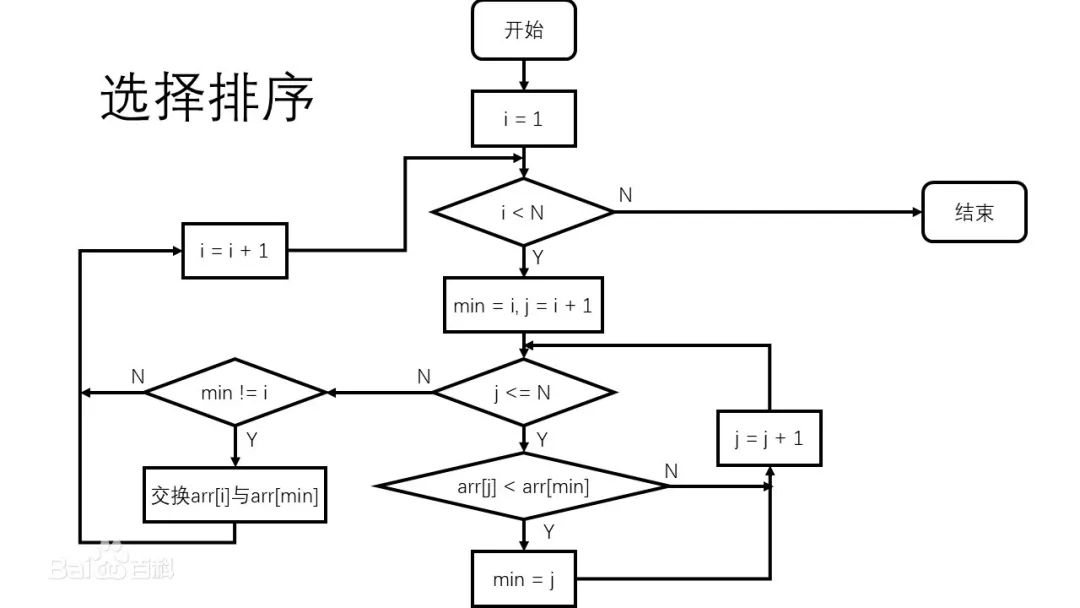
比如有這樣一個數組，先把它畫成一顆二叉樹的形式，接下來就是構建大頂堆，這個部分也是整個堆排序中最耗時的部分。

從0這個節點開始，因為節點0是最后一個有孩子的節點。

0比2小，交換一下位置。

再輪到4，8和9比較，顯然是9大，把9和4交換一下位置。

最后輪到3，9比2大，9和3需要交換一下位置。

注意，因為這個節點發生了變化，所以3 8 4不再滿足條件，還得繼續調整。8比4大，8和3交換一下位置。

這個過程就是構建大頂堆。

于是，我們得到了最大的數字9，把它和最后一個數字做交換，然后斷開，意思就是后面的操作跟9沒有關系了。

接下來就是調整大頂堆，不需要再像剛才那樣構建，因為這顆二叉樹也只有根節點被修改了。

0和8交換，4和0交換，又得到了第二大的數字8。

不斷的重復，最后就是一個有序的序列。

寫代碼之前，還得明確一個問題，雖然我們一直在操作二叉樹，但是寫代碼的時候并不需要真的去創建一顆二叉樹，我們只是在操作數組的下標，比如下標為n的節點作為根幾點，那么他的左孩子就是 2n+1，右孩子就是2n+2。

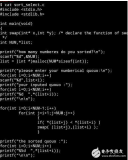
#include 


void adjust_heap_sort(int *a, int root, int last)
{
    int child;


    while (1)
    {
        child = 2 * root + 1;
        if (child > last)
            break;


        if (child + 1 <= last && a[child] < a[child + 1])
        {
            child++;
        }


        if (a[child] > a[root])
        {
            int num = a[root];
            a[root] = a[child];
            a[child] = num;
        }


        root = child;
    }
}


void heap_sort(int *a, int size)
{
    //構建大頂堆
    for (int i = size / 2 - 1; i >= 0; i--)
    {
        adjust_heap_sort(a, i, size - 1);
    }


    //調整大頂堆
    for (int i = size - 1; i > 0; i--)
    {
        int num = a[0];
        a[0] = a[i];
        a[i] = num;


        adjust_heap_sort(a, 0, i - 1);
    }
}


int main()
{
    int array[] = {3, 4, 0, 8, 9, 2};


    heap_sort(array, 6);


    for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++)
    {
        printf("%d ", array[i]);
    }
    printf("
");


    return 0;
}

代碼確實不太容易理解，不過在這些排序算法中，越是不容易理解的，效率也就越高，還是用它和冒泡做個對比，10000個數據，差距還是很大的。

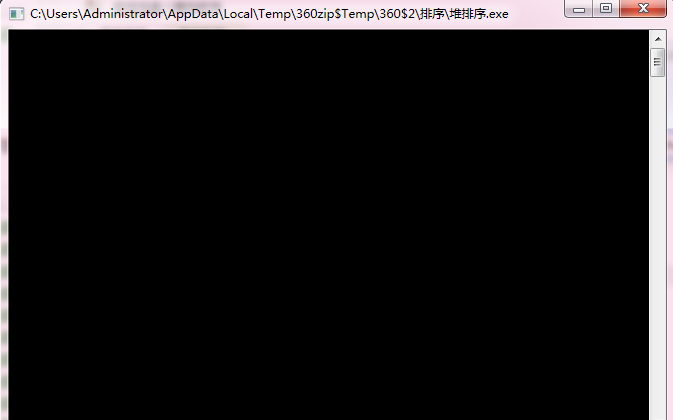
root@Turbo:test# time ./heap_sort 


real  0m0.005s
user  0m0.004s
sys  0m0.000s
root@Turbo:test# time ./bubble_sort 


real  0m0.606s
user  0m0.554s
sys  0m0.000s
root@Turbo:test#

審核編輯：劉清