在現代智能控制算法中，模糊控制是在實際控制系統設計中使用比較成熟的一種方法。模糊控制可以使用在一些無法建立系統模型的場合，根據專家經驗確定模糊規則，實現對系統的控制。

WM算法是一種一種基本的模糊控制算法。該算法的思想是根據采樣的數據對（一組輸入、輸出數據），確定出模糊規則，通常是一條數據對就確定一條規則。

首先我們需要確定系統的輸入輸出數量，假設系統為單輸入單輸出。對輸入變量x，輸出變量y分別劃分模糊集合，可以使用正態分布隸屬度函數，或者三角隸屬度函數來劃分。這叫做變量的模糊化。如x的論域為[0,2]，劃分13個模糊集合，分別為A1~A13，如下圖所示。

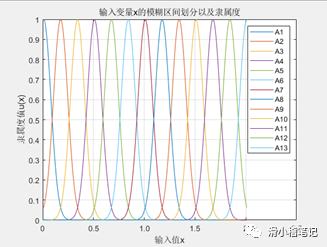
對于輸出y，論域為[-1.5,1.5]，劃分13個模糊集合，為B1~B13，如下圖所示。

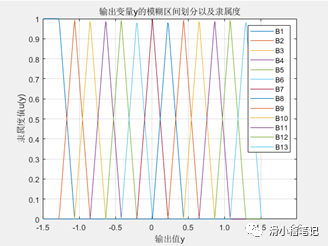
現在有0-2論域上均勻分布的樣本點共21個，利用它們來確定模糊規則。

需要分別計算每一個數據點在模糊集合上的隸屬度，選取最高的隸屬度值作為確定一條模糊規則的依據。如樣本點（0.2，1），需要計算0.2在輸入隸屬度函數中的隸屬度值，需要計算13個值，找出其中最大的值如A5，則輸入為A5，再計算輸出1在13個模糊集合中的隸屬度函數值，找出最大的那個，如B2，則輸出為B2，由此可以確定一條模糊規則：IF x=A5 THEN y=B2，由此可以確定21個規則；但是這些規則有大量的重復和沖突的規則，需要計算它們置信度

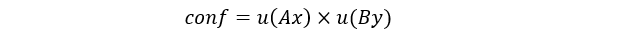
由此公式可以求出矛盾規則的置信度，把置信度低的規則去掉；按照WM算法的提出則王立新的做法，還應該乘上一個專家經驗系數，也就是專家認為這條規則的可信度大不大。上面的公式改寫為：

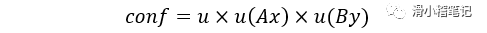
由此建立了模糊規則庫

上面表中的第一行代表輸入x的隸屬集合的下標，第二行代表輸出y的隸屬集合的下標。利用模糊規則庫，計算輸出y。根據去模糊化公式即可計算輸出值：

（1）計算輸出變量y的隸屬度函數值，創建u_y_B.m文件輸入以下代碼：

%y:輸出變量的值
%a:區間中點的值
%left:表示論域區間的左端點
%right:表示論域區間的右端點
%step:三角形底邊長的一半
function u = u_y_B( y, a, left, right, step )
b = a-step ;
c = a+step ;
len = length( y ) ;
u = zeros( 1, len ) ;
for i = 1: len
    if a==left+step
        if y(i)>=b && y(i)<=a
            u(i) = 1 ;
        end
        if y(i)>a && y(i)<=c
            u(i) = ( c-y(i) )/( c-a ) ;
        end
        if y(i)y(i)>c
            u(i) = 0 ;
        end
    elseif a==right-step
        if y(i)>=b && y(i)<=a
            u(i) = ( y(i)-b )/( a-b ) ;
        end
        if y(i)>a && y(i)<=c
            u(i) = 1 ;
        end
        if y(i)y(i)>c
            u(i) = 0 ;
        end
    else
        if y(i)>=b && y(i)<=a
            u(i) = ( y(i)-b )/( a-b ) ;
        end
        if y(i)>a && y(i)<=c
            u(i)=( c-y(i) )/( c-a ) ;
        end
        if y(i)y(i)>c
            u(i) = 0 ;
        end
    end
end
end

（2）計算輸入隸屬度（輸入模糊化），創建u_x.m文件輸入以下代碼：

%x:輸入值
%u:輸出一個有隸屬度組成的數組
function u = u_x( x )
a = 0 ;
u = zeros( 1, 10 ) ;
for i = 1: 10
    a = a + 0.2 ;
    u(i) = u_x_A( x, a ) ;
end
end

（3）計算輸入變量x的隸屬度函數值，創建u_x_A.m文件輸入以下代碼：

%x:輸入變量的值
%a:區間中點的值
function u = u_x_A( x, a )
len = length( x ) ;
u = zeros( 1, len ) ;
b = a - 0.2 ;
c = a + 0.2 ;
for i=1:len
    if a==0.2
        if x(i)>=b && x(i)<=a
            u(i) = 1 ;
        end
        if x(i)>a && x(i)<=c
            u(i)=( c-x(i) )/( c-a ) ;
        end
        if x(i)i)>c
            u(i) = 0 ;
        end
    elseif a==1.8
        if x(i)>=b && x(i)<=a
            u(i) = ( x(i)-b )/( a-b ) ;
        end
        if x(i)>a && x(i)<=c
            u(i) = 1 ;
        end
        if x(i)i)>c
            u(i) = 0 ;
        end
    else
        if x(i)>=b && x(i)<=a
            u(i) = ( x(i)-b )/( a-b ) ;
        end
        if x(i)>a && x(i)<=c
            u(i) = ( c-x(i) )/( c-a ) ;
        end
        if x(i)i)>c
            u(i) = 0 ;
        end
    end
end
end

（4）WM算法實現腳本，創建test01.m文件并輸入以下代碼：

clc
clear
%繪制原始圖像
t = 0: 0.01: 2;
y = 0.9*sin( pi*t )+0.3*cos( 3*pi*t );
plot( t, y );
grid on;
xlabel( 'ê?3??μx' ) ;
ylabel( 'ê?è??μy' ) ;
title( 'y=0.9*sin(pi*t)+0.3*cos(3*pi*t)' ) ;
%獲取采樣點
sample_x = 0: 0.1: 2;
sample_y = 0.9*sin( pi*sample_x )+0.3*cos( 3*pi*sample_x  );
sample_num = length( sample_x ) ;                                 %計算采樣個數
% %論域x劃分set_X個模糊區間,使用高斯隸屬函數,論域[0,2]
set_X = 13 ;
xmin = 0 ;
xmax = 2 ;
x_step = ( xmax-xmin )/( set_X-1 ) ;                              %x模糊集合的步長
av_x = xmin: x_step: xmax;                                          %計算高斯分布均值
sigma_x = sqrt( -x_step^2/( 8*log( 0.5 ) ) ) ;                  %計算高斯分布方差
%繪制x的模糊函數曲線
x = xmin: 0.01: xmax ;
figure( 2 )
for i=1:set_X
    plot( gaussmf( x, [ sigma_x, av_x(i) ] ) ) ;
    hold on;
end
grid on;
legend( 'A1','A2','A3','A4','A5','A6','A7','A8','A9','A10','A11','A12','A13' ) ;
xlabel( '輸入值x ' );
ylabel( '隸屬度值u (x)' );
set( gca,'XTick', 0:50:250 ) ;
set( gca,'XTickLabel', {'0','0.5','1.0','1.5','2','2.5'} ) ;
title( '輸入變量x的模糊區間劃分以及隸屬度' ) ;
%論域y劃分set_Y模糊區間,使用三角隸屬函數,論域[-1.5,1.5]
set_Y = 13 ;
ymin = -1.5 ;
ymax = 1.5 ;
y_step = ( ymax-ymin )/( set_Y+1 ) ;                            %y模糊集合的步長
a = ymin ;                                                           %保存論域下限
%繪制y的模糊函數曲線
y = ymin: 0.01: ymax ;                                             %獲取一組y的數值
figure( 3 )
for i=1:set_Y
    a = a+y_step ;
    plot( u_y_B( y, a, ymin, ymax, y_step ) ) ;                %繪制y的模糊函數曲線
    hold on ;
end
grid on;
legend( 'B1','B2','B3','B4','B5','B6','B7','B8','B9','B10','B11','B12','B13' ) ;
xlabel( '輸出值y' );
ylabel( '隸屬度值u(y)' );
set( gca, 'XTick', 0:50:350 ) ;
set( gca, 'XTickLabel', {'-1.5','-1.0','-0.5','0','0.5','1.0','1.5','2.0'} ) ;
title( '輸出變量y的模糊區間劃分以及隸屬度' ) ;
% WM算法
uxA = zeros( sample_num, set_X ) ;                               %存儲每條樣本數據x的隸屬度函數值
uyB = zeros( sample_num, set_Y ) ;                               %存儲每條樣本數據y的隸屬度函數值
for i=1:set_X
    uxA( :, i ) = gaussmf( sample_x, [ sigma_x, av_x(i) ] ) ;%樣本x在第i個模糊區間的隸屬度值
end
a = ymin ;
for i=1:set_Y
    a = a+y_step ;
uyB( :, i ) = u_y_B( sample_y, a, ymin, ymax, y_step ) ; %樣本y在第i個模糊區間的隸屬度值
end
WM_rule = zeros( 3, sample_num ) ;                                %保存樣本數據所在模糊集合下標
[ ~, WM_rule(1,:) ] = max( uxA, [], 2 ) ;                       %計算每個樣本x所在的模糊集合下標
[ ~, WM_rule(2,:) ] = max( uyB, [], 2 ) ;                       %計算每個樣本y所在的模糊集合下標
 for i=1:sample_num
    WM_rule(3,i) = uxA( i,WM_rule(1,i) )*uyB( i,WM_rule(2,i) ) ;%計算每條規則的有效性
 end
 %去除信任度低的規則
 for i = 2:sample_num
    if WM_rule( 1, i-1 )==WM_rule( 1, i )
        if WM_rule( 3, i-1 )<=WM_rule( 3, i )
            WM_rule( :, i-1 ) = 0 ;
        else
            WM_rule( :, i ) = 0 ;
        end
    end
 end
WM_rule( :, all( WM_rule==0,1 ) ) = [] ;                            %去除多于的規則

（5）WM算法測試腳本，創建test02.m文件并輸入以下代碼：

p_value = zeros( 1, set_Y ) ;                        %用于保存y模糊函數尖點所對應的橫坐標的值
a = ymin ;
for i = 1: set_Y
    a = a + y_step ;
    p_value( i ) = a ;                                 %保存y模糊函數尖點所對應的橫坐標的值
end
%測試規則
x = 0 ;
WM_y_x = zeros( 1, 201 ) ;
for i = 1: 201
    x = x + 0.01 ;
    ux = zeros ( 1, set_X ) ;
    for j = 1: set_X
        ux(j) = gaussmf( x, [ sigma_x, av_x(j) ] ) ;
    end
    num = 0 ;
    den = 0 ;
    for j = 1: set_X
        num = num + p_value( WM_rule( 2, j ) )*ux(j);
        den = den + ux(j) ;
    end
    WM_y_x(i) = num/den ;
end
figure(4);
%繪制WM算法的輸出曲線
x = 0: 0.01: 2 ;
plot( x, WM_y_x, '-.b' ) ;
hold on ;
y = 0.9*sin( pi*x )+0.3*cos( 3*pi*x ) ;
%畫出原始函數的曲線
plot( x, y, '-g' ) ;
xlabel( '輸入值x ' ) ;
ylabel( '輸出值y' ) ;
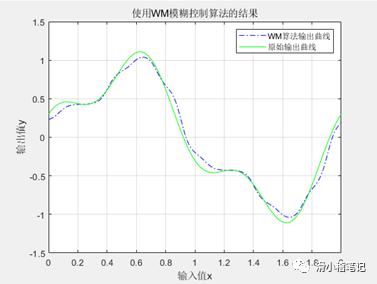
title( '使用WM模糊控制算法的結果' ) ;
legend( ' WM算法輸出曲線','原始輸出曲線' ) ;
grid on ;

運行結果如下圖所示。