通過傳輸線、方程和示例波形了解射頻 (RF) 波的傳播和反射。
自然界中各種類型的波基本上表現得相似。就像一個聲音,在懸崖上回蕩, 電波 當他們遇到變化時進行反思 阻抗 他們旅行的媒介。波反射可以導致一種有趣的現象,稱為 駐波.駐波對于大多數樂器產生聲音的方式至關重要。例如,如果沒有駐波的可預測性和放大效應,弦樂器將無法工作。
然而,在RF設計中,當我們的目標是將功率從一個模塊傳輸到信號鏈中的下一個模塊時,駐波是不可取的。事實上,駐波會影響不同射頻和微波系統的性能,從 消聲室到微波爐等日常電器。
雖然波傳播和反射的概念并不是非常復雜,但一開始可能有點令人困惑。可視化波如何傳播和反射不連續性的最佳方法是繪制不同配置的波動方程。
在本文中,我們將首先推導出所需的方程,并使用它們通過幾個示例波形來解釋駐波現象。
傳輸線電壓和電流波方程
首先,讓我們推導出我們的方程。我知道這很無聊,但它們確實幫助我們理解波是如何傳播和相互作用的。 傳輸線.在本系列的上一篇文章中,我們研究了傳輸線的正弦穩態響應,并推導出了電壓和電流方程。應用 vs(t) = Vscos(ωt) 到一行, 電壓和電流 波是:
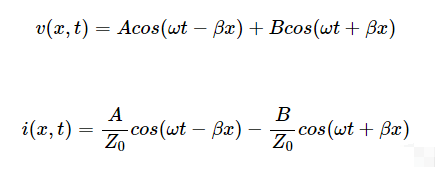
哪里:
A 和 B 是從線路輸入和輸出端口的邊界條件中找到的常數
Z0是特性阻抗
相位常數β
這些方程對應于圖1(a)所示的配置,其中選擇從源到負載的正x軸方向。如果我們用它們的相量表示這些波,則正行(或入射)波和后行進(或反射)電壓波將分別為 Ae-jβx和成為jβx,如圖1(a)所示。
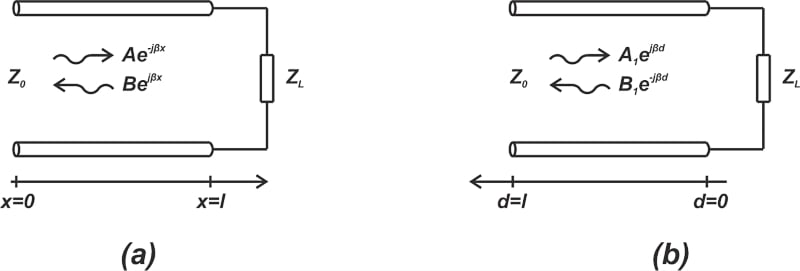
圖1.顯示正軸方向的圖表是從源到荷載 (a),然后從荷載到源 (b)。
關于傳輸線問題,通常選擇從負載到源的正軸方向更為方便,如圖1(b)所示。為了找到新的方程,我們需要用l-d替換原始方程中的x。如新變量 d 所示,前行波變為:
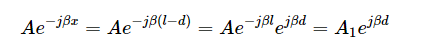
其中 A1= Ae-jβl是一個新常量。從這里,您可以驗證在新坐標系中反射波是否為 B1e-jβd,其中 B1= 是JΒL.因此,總電壓和電流相量如公式1和2所示。
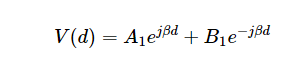
等式 1.
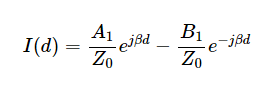
等式 2.
這些方程可以更輕松地檢查載荷對波反射的影響,因為在這種情況下,載荷在d = 0,從而簡化了方程。設d = 0,在負載端得到以下方程,如公式3和4所示。
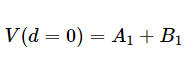
等式 3.
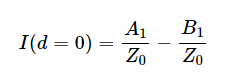
等式 4.
例如,讓我們考慮線路在開路中終止的情況。輸出開路時(ZL=∞),輸出電流明顯為零。從公式 4 中,我們得到1= B1,因此,總電壓為 V(d = 0) = 2A1.
因此,對于開路線路,反射電壓等于輸出端的入射電壓,此時的總電壓是入射電壓的兩倍。同樣,我們可以使用等式 3 和 4 來求任意負載阻抗 Z 的反射波與入射波之比L.該比率是一個重要的參數,稱為 反射系數,我們很快就會介紹。
輸入阻抗和反射系數公式
使用公式1和2,我們可以找到沿線不同點的電壓與電流之比(即傳輸線的輸入阻抗)。這就引出了公式5。
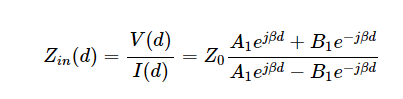
等式 5.
注意線路負載端的線路阻抗(d = 0)等于負載阻抗ZL,我們得到:
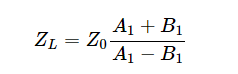
使用一點代數,上面的方程給出了反射電壓波與入射電壓波的比值(B1/一個1),定義為公式6中Γ的反射系數。
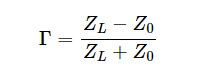
等式 6.
上面的討論表明,對于終止的線路,入射波和反射波之間存在明確的關系。請注意,一般來說,反射系數是一個復數,Γ的幅度和相位信息都很重要。為 電力傳輸,我們嘗試獲得匹配的負載 (ZL= Z0),導致 Γ = 0。在這種情況下,施加到輸入端的波被負載完全吸收,不會發生反射。在這里考慮另外兩種特殊情況是有益的: 開路線路和短路 我們很快就會進入的行。
雖然波傳播和反射的概念基本上并不復雜,但一開始可能會令人困惑。可視化波如何傳播和反射不連續性的最佳方法是繪制我們上面開發的方程。此外,值得一提的是,有許多在線模擬器可以幫助您更好地了解波傳播概念。
短路線路
接下來,讓我們來看看短路線。發生短路時,總輸出電壓應始終為零。此外,從公式6中,我們有Γ = -1。入射電壓波由下式給出:
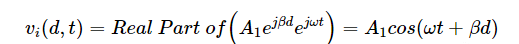
圖 2 中的頂部曲線提供了該方程在三個不同時間點 t 處的曲線1, t2和 t3,其中 t1< t2?< t3.
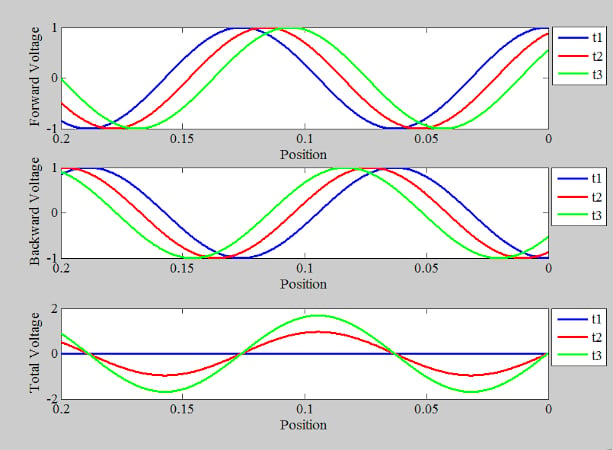
圖2.短路的正向電壓(頂部)、反向電壓(中間)和總電壓(底部)的示例曲線。
上述曲線細分其中:
輸電線路長度0.2米
負載在 d = 0
β為50弧度/米
信號頻率為 2 GHz
請注意入射波如何隨著時間的流逝逐漸向負載移動(d = 0)。上圖中的中間曲線顯示了遠離負載的反射電壓。反射電壓方程為:
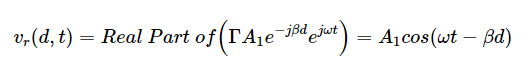
其中Γ設置為 -1 以考慮短路。總電壓是入射電壓和反射電壓之和,在下部曲線中給出。正向電壓在沿線路的所有點(包括線路的負載端)在其最小值和最大值之間波動。但是,反射電壓取與入射電壓相反的值,因此負載端的總電壓始終為零。
總電壓波有一個有趣的特征:它靜止不動,與其組成波不同,總電壓波不向任一方向傳播。例如,最大和零電壓點不隨時間移動。為了更好地說明這一點,圖3繪制了36個不同時間點的總電壓。
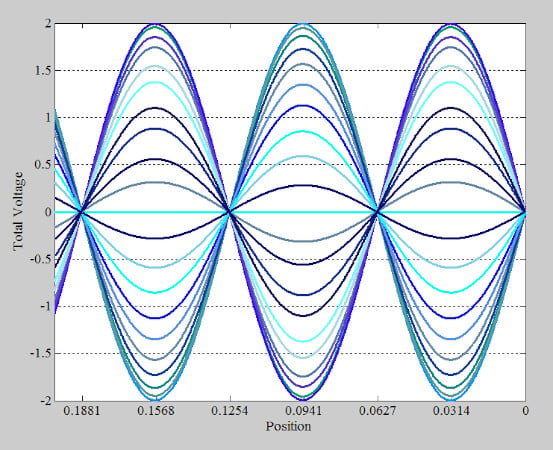
圖3.顯示 36 個不同時間點的總電壓的圖。
可以看出,過零點(節點)和最大振幅的位置(反節點)是沿線的一些固定位置。由于波不向任一方向傳播,因此稱為駐波。
開路線路
對于開路線路(ZL= ∞),公式 6 得到 Γ = 1。在這種情況下,反射電壓的幅度和相位等于入射電壓。圖4中的頂部和中間曲線分別顯示了三個不同時間點開路線路上的入射和反射電壓波。
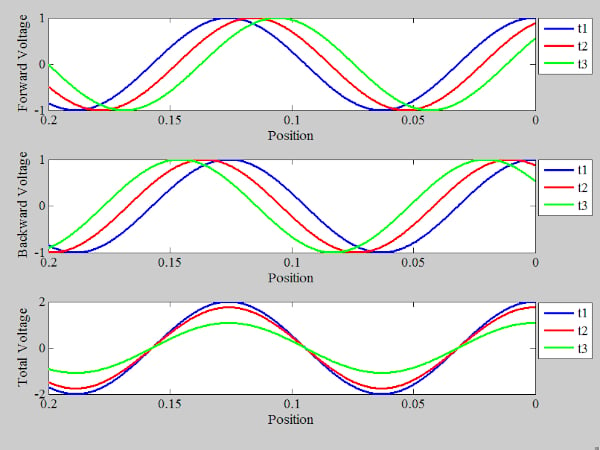
圖4.顯示開路的正向電壓(頂部)、反向電壓(中間)和總電壓(底部)的示例圖。
請注意,入射波和反射波在 d = 0 時具有相同的值。因此,總電壓(底部曲線)是負載端入射電壓的兩倍。由于Γ = 1,反射電流Ir也具有與入射電流I相同的幅度和相位我.但是,總電流為 I我-我r負載端 = 0,這并不奇怪,因為負載是開路的。
此外,我們可以再次觀察到總電壓是駐波。圖5對此進行了最好的說明,它繪制了36個不同時間點的總電壓波。
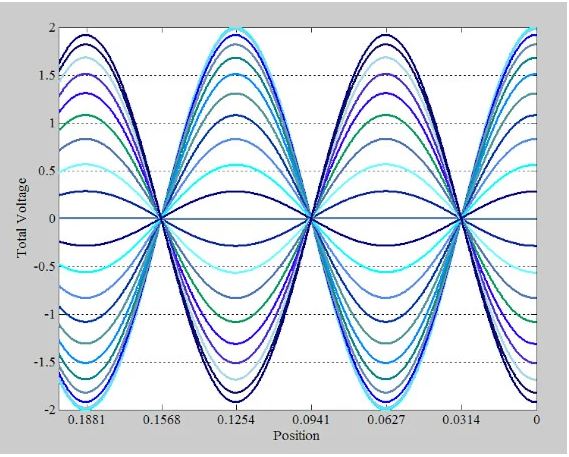
圖5.示例圖顯示了開路 36 個不同時間點的總電壓波。
計算端接線路的任意負載
接下來,讓我們使用我們的方程來檢查 Γ = 0.5 的終止線。任意時間的入射和反射電壓波如圖6所示。
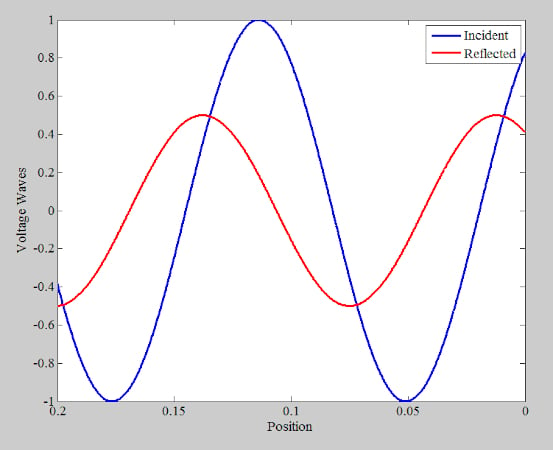
圖6.顯示入射和反射電壓波的圖。
這兩個波浪以相反的方向傳播。您應該能夠想象,在沿線的某個時間點和某個特定位置,兩個波的峰值將重合,從而產生總電壓波的最大值。如圖 7 所示。
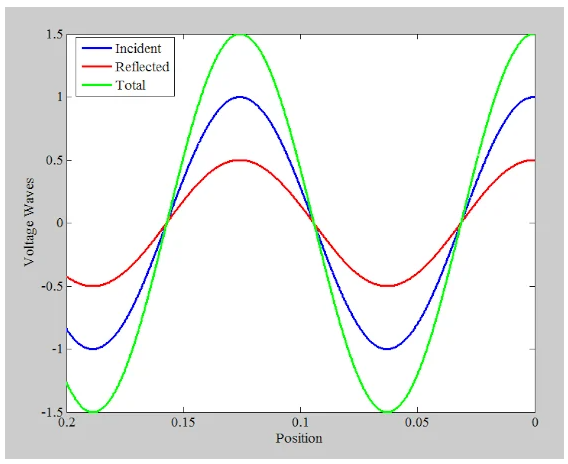
圖7.示例圖顯示了入射波和反射波峰值重合時總電壓波的最大值。
此外,在其他某個時間點,沿線的特定位置將“看到”較浪的峰值和較小波浪的最小值,如圖 8 所示。
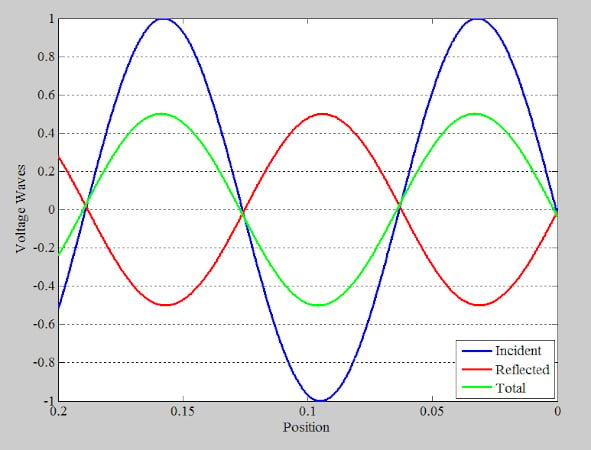
圖8.顯示入射波和反射波具有相反的波峰和谷的總電壓波的示例圖。
在這些點上,總電壓波的幅度最小。在我們的示例中,正向波和反射波的振幅分別為 1 和 0.5。因此,總電壓波的最小振幅為1 - 0.5 = 0.5。為了更好地觀察沿線不同點的電壓幅度,圖9繪制了36個不同實例的總電壓波。
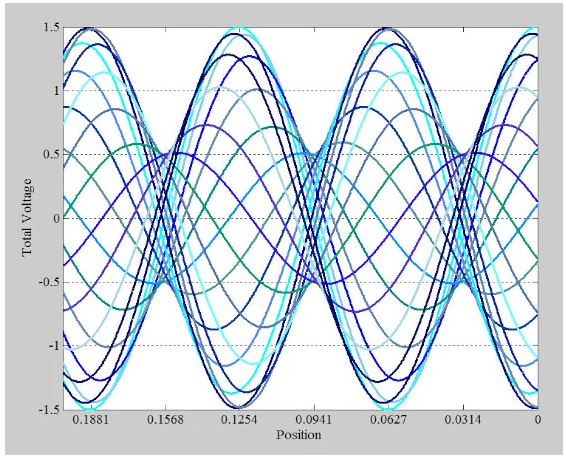
圖9.示例圖顯示了 36 個不同實例的總電壓波。
該圖可讓您了解線上不同點的波動幅度。請注意,雖然d = 0.1881 m等點在±1.5 V之間波動,但還有其他點。例如,d = 0.1568 m,其振幅要小得多,并且在±0.5 V之間波動。
你可能會問的一個問題是,總波是行進還是靜止不動?圖10顯示了某些連續時間點的總電壓曲線數量較少(t1< 噸2?< ...< 噸6) 來回答這個問題。???
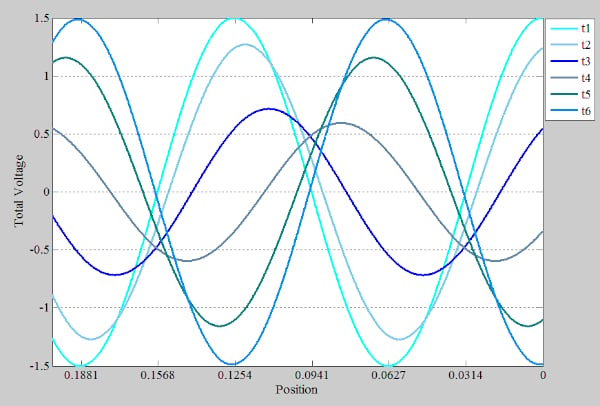
圖 10.顯示連續時間點總電壓曲線較少的示例。
該圖顯示,隨著時間的流逝,波向負載傳播。請注意,雖然入射波和反射波的幅度是恒定的,但組合電壓的幅度會隨著時間的推移而上升和下降。
入射波、反射波和駐波摘要
讓我們總結一下我們的觀察結果:
在匹配負載下,入射波向負載傳播,并且沒有反射。在這種情況下,波沿線具有恒定的振幅。
對于短路和開路線路,入射波完全反射(Γ = -1或1)。在這種情況下,組合電壓不沿任一方向傳播,稱為駐波。
對于駐波,我們在沿線的固定位置有節點和反節點。節點根本不波動,而反節點以最大振幅波動。
對于上述三種情況以外的載荷,我們有一個隨時間上升和下降的行波(盡管它實際上是一個行波,但我們可能偶爾會輕描淡寫地將這個波稱為駐波)。在這種情況下,我們沒有任何節點,但某些點的振幅比其他點小。這種情況介于無反射的理想情況 (Γ = 0) 和全反射的最壞情況 (Γ = ±1) 之間。
因此,考慮到所有這些,我們必須知道我們的傳輸線在這個頻譜的哪個點上運行。參數 駐波比(電壓駐波比),定義為波的最大振幅與其最小振幅的比值,使我們能夠表征我們離駐波有多近。當有全反射時,駐波比是無限的;對于匹配的負載,駐波比為 1。
至于其他情況,VSWR介于這兩個極值之間。VSWR為我們提供了一種表征反射量的替代方法。
-
射頻
+關注
關注
104文章
5573瀏覽量
167694 -
RF
+關注
關注
65文章
3050瀏覽量
166963 -
傳輸線
+關注
關注
0文章
376瀏覽量
24022 -
RF設計
+關注
關注
1文章
27瀏覽量
13091 -
駐波
+關注
關注
0文章
9瀏覽量
9633
發布評論請先 登錄
相關推薦
PCB傳輸線之SI反射問題的解決
傳輸線阻抗不匹配的情況下,反射系數的正負與反射波相位的關系
請問脈沖經過傳輸線反射后為啥和理論不一樣
分析一下反射的機理、反射系數和傳輸系數的計算
信號完整 性--傳輸線與反射
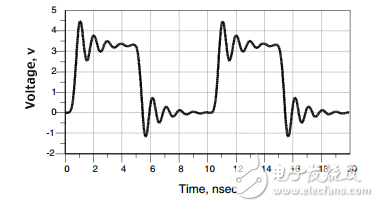
不同的反射系數,信號的是怎樣的呢?
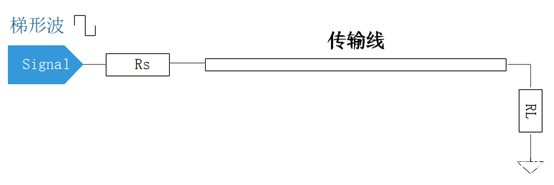




 傳輸線理論:觀察反射系數和駐波
傳輸線理論:觀察反射系數和駐波










評論