***11 ***訓練神經網絡 第二部分
現在我們有了一個明確的目標:最小化神經網絡的損失。通過調整網絡的權重和截距項,我們可以改變其預測結果,但如何才能逐步地減少損失?
這一段內容涉及到多元微積分,如果不熟悉微積分的話,可以跳過這些數學內容。
為了簡化問題,假設我們的數據集中只有Alice:
假設我們的網絡總是輸出0,換言之就是認為所有人都是男性。損失如何?

那均方差損失就只是Alice的方差:
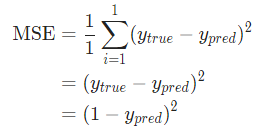
也可以把損失看成是權重和截距項的函數。讓我們給網絡標上權重和截距項:
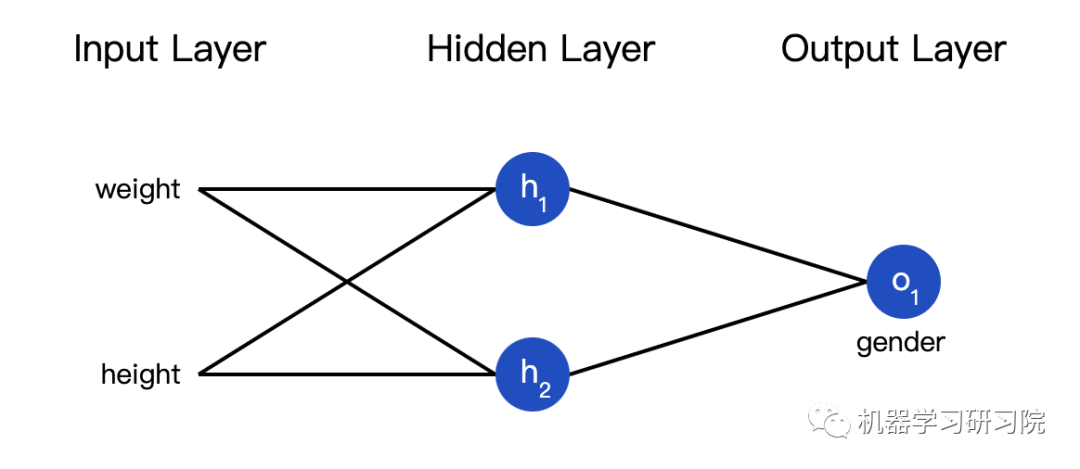
這樣我們就可以把網絡的損失表示為:
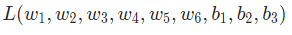
假設我們要優化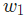 ,當我們改變
,當我們改變 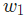 時,損失
時,損失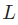 會怎么變化?可以用
會怎么變化?可以用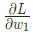 來回答這個問題,怎么計算?
來回答這個問題,怎么計算?
接下來的數據稍微有點復雜,別擔心,準備好紙和筆。
首先,讓我們用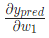 來改寫這個偏導數:
來改寫這個偏導數:
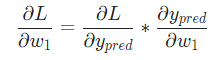
因為我們已經知道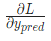 ,所以我們可以計算
,所以我們可以計算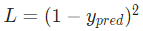
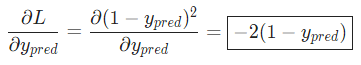
現在讓我們來搞定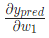 。
。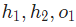 分別是其所表示的神經元的輸出,我們有:
分別是其所表示的神經元的輸出,我們有:
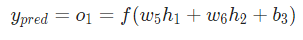
由于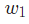 只會影響
只會影響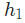 (不會影響
(不會影響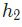 ),所以:
),所以:
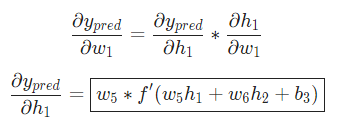
對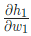 ,我們也可以這么做:
,我們也可以這么做:
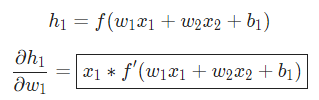
在這里,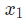 是身高,
是身高,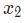 是體重。這是我們第二次看到
是體重。這是我們第二次看到 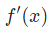 (S型函數的導數)了。求解:
(S型函數的導數)了。求解:
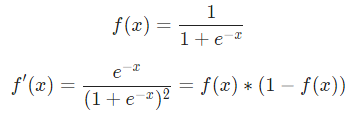
稍后我們會用到這個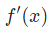 。
。
我們已經把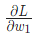 分解成了幾個我們能計算的部分:
分解成了幾個我們能計算的部分:
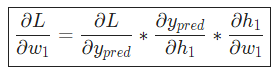
這種計算偏導的方法叫『反向傳播算法』(backpropagation)。
好多數學符號,如果你還沒搞明白的話,我們來看一個實際例子。
***12 ***例子:計算偏導數
我們還是看數據集中只有Alice的情況:

把所有的權重和截距項都分別初始化為1和0。在網絡中做前饋計算:
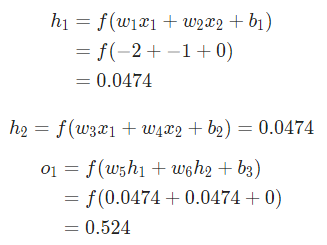
網絡的輸出是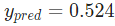 ,對于Male(0)或者Female(1)都沒有太強的傾向性。算一下
,對于Male(0)或者Female(1)都沒有太強的傾向性。算一下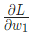
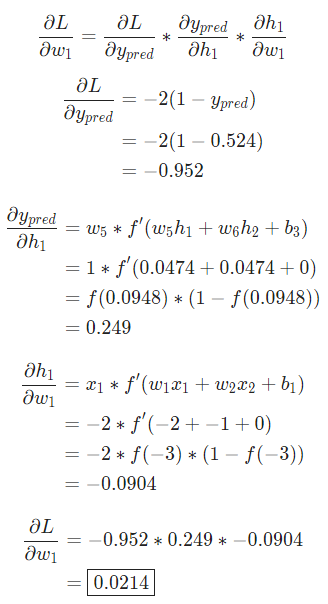
提示: 前面已經得到了S型激活函數的導數 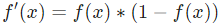 。
。
搞定!這個結果的意思就是增加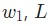 也會隨之輕微上升。
也會隨之輕微上升。
***13 ***訓練:隨機梯度下降
現在訓練神經網絡已經萬事俱備了!我們會使用名為隨機梯度下降法的優化算法來優化網絡的權重和截距項,實現損失的最小化。核心就是這個更新等式:
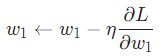
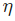 是一個常數,被稱為學習率,用于調整訓練的速度。我們要做的就是用
是一個常數,被稱為學習率,用于調整訓練的速度。我們要做的就是用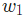 減去
減去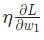
- 如果
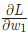 是正數,
是正數,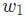 變小,
變小,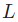 會下降。
會下降。 - 如果
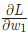 是負數,
是負數,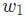 會變大,
會變大,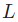 會上升。
會上升。
如果我們對網絡中的每個權重和截距項都這樣進行優化,損失就會不斷下降,網絡性能會不斷上升。
我們的訓練過程是這樣的:
- 從我們的數據集中選擇一個樣本,用隨機梯度下降法進行優化——每次我們都只針對一個樣本進行優化;
- 計算每個權重或截距項對損失的偏導(例如
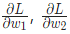 等);
等); - 用更新等式更新每個權重和截距項;
- 重復第一步;
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100715 -
神經元
+關注
關注
1文章
363瀏覽量
18449 -
python
+關注
關注
56文章
4792瀏覽量
84628
發布評論請先 登錄
相關推薦
labview BP神經網絡的實現
【PYNQ-Z2試用體驗】神經網絡基礎知識
卷積神經網絡如何使用
【案例分享】ART神經網絡與SOM神經網絡
人工神經網絡實現方法有哪些?
如何構建神經網絡?
基于BP神經網絡的PID控制
卷積神經網絡一維卷積的處理過程
用Python從頭實現一個神經網絡來理解神經網絡的原理1
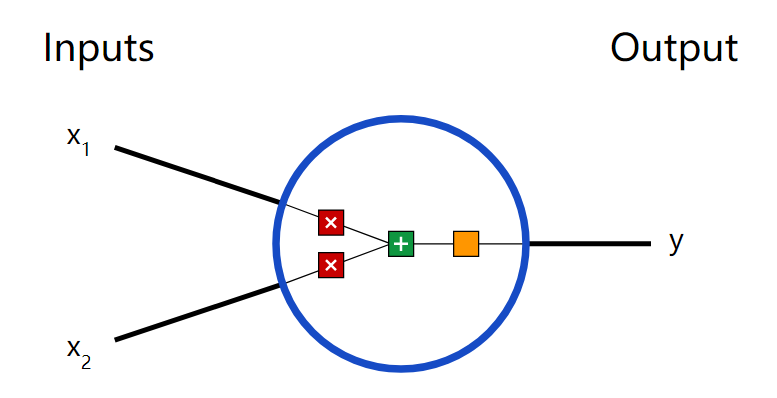
用Python從頭實現一個神經網絡來理解神經網絡的原理2
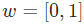
用Python從頭實現一個神經網絡來理解神經網絡的原理4





 用Python從頭實現一個神經網絡來理解神經網絡的原理3
用Python從頭實現一個神經網絡來理解神經網絡的原理3










評論