1、前言
最近弄了點小項目,關于單目立體視覺的,目的是對單目下的物體體積進行解算。對這件事我個人覺得這是一個很有意思的話題,查閱了一些相關的文章,做單目立體視覺的高校、公司都還很多。比如說2021年北方工業(yè)大學的一篇碩士論文中進行了與此相關的技術研究,如果沒記錯的話,清華大學做過輔助激光實現(xiàn)的立體圓柱體積測量,蘇州大學也完成了類似的單目體積測量研究。當然目前也有很多的深度相機可能可以直接通過讀數(shù)完成對目標的測量,但是對立體視覺的研究思考,空間的轉(zhuǎn)換關系依然是一個重要的課題。
一般而言,單目是無法依靠自身來完成測量的,有企業(yè)選擇讓單目相機動起來,但是一旦動起來實際上也是雙目,不再是單目。其實單目最大的問題是缺少了深度信息。近大遠小是我們最常用的成像規(guī)律,近處物體在視場中占比大,遠處物體在視場中占比小。因此,我們需要些方法來彌補缺失的深度信息。從硬件角度上可以輔佐以激光、結(jié)構(gòu)光等等,這都是比較常用的輔助手段,三維成像上來說線結(jié)構(gòu)光對掃描結(jié)構(gòu)重構(gòu)技術也已經(jīng)相對比較完善了。因此在解決單目立體視覺問題下的輔助手段問題,我是打算將目標置于標準平臺上,利用標準平臺的數(shù)據(jù)來對相機進行標定,從而構(gòu)建我需要的視場參數(shù),進而求解。圖1是我利用工業(yè)相機與鏡頭在一塊標準平臺的方塊采集結(jié)果。在標準平臺上,底面的洞洞空,空間距離為2.5 cm。

圖1 實物圖與采集現(xiàn)場
視覺測量中一般的步驟是圖像采集、標定、目標提取、像素長度角度提取以及最后的實際長度解算過程。
有時候會覺得自己很耍賴,用工業(yè)相機加定焦鏡頭這種畸變很小的方式做圖像測量實驗很玩賴(還選了對圖像處理最為有利的打光方式)~如果在要求精度不高的情況下,確實很容易得到無畸變下圖像的具體尺寸,但是我又覺得逐步的提高精度,才是視覺測量該有的樣子,相比于利用各種花式的測量方法,難道大家利用圖像的原因不就是因為可以到1 um,2 um的測量精度與一整個平面的采集效果嘛~當然以上都是題外話的隨筆,下面還要接著介紹一些標定求解的思路。

圖2 目標背景點提取
2、部分理論分析
圖2是目標背景點的提取情況,利用圖像處理的手段將目標背景中的每一橫行的縱向距離提取出來,從圖像上也能看出來距離鏡頭近的地方兩個橫行之間距離長,距離鏡頭遠的地方距離短,這是很符合近大遠小的規(guī)律的。那么我到底要標定求解什么呢?
普適意義上的標定一般上都是遵循張氏標定法,將空間坐標系與圖像坐標系之間的關系用矩陣的方式寫出來,這其中主要是涉及到兩個重要參數(shù),一個是相機內(nèi)參,一個是相機外參。內(nèi)參數(shù)一般包括了相機的像元尺寸、相機的畸變情況;外參代表了相機與目標的空間位置。因此既然我能得到空間位置就一定可以得到成像平面的相關數(shù)據(jù),那么體積的求解似乎就變得沒那么難了。但是標定并不是一成不變的,不同位置的標定結(jié)果顯然是不一樣的,不同深度的標定結(jié)果也不一樣,這其中就有人考慮,是不是可以把標定靶直接和目標粘連在一起?那么確實存在這樣一種方案可以實現(xiàn),這種方法叫合作目標標定測量。
而我想寫下的是更基礎一點的一些標定思路,我也是在沒有用張氏標定法情況下用固定平面作為標定靶來做體積測量。
我分析了一些問題,首先,近大遠小的根本原因是什么?在不考慮畸變的前提下,我覺得是因為在相機深度范圍內(nèi),物距變大了,導致光學放大倍數(shù)變小了,或者說單個像元的尺寸當量變大了。遠處尺寸當量大,那么相同像元個數(shù)下,視場變大,遠處的目標在視場中占比就變小,近大遠小,自此而來。那么第二個問題就來了,像元尺寸當量的變化規(guī)律是怎么樣的呢?在張氏標定法中給出的旋轉(zhuǎn)矩陣來看,好像是一次線性關系,那如何推導呢?第三個問題,實際上的像素尺寸乘以像素當量就是我要得結(jié)果了嘛?顯然不是,還需要與我的鏡頭成像夾角有關系~
基于上一段的分析,我得出這樣一些簡單的思考結(jié)論:
(1)我默認了成像時沒有畸變的,因此在求解上不考慮桶形畸變的補償問題;
(2)我默認了相機在橫向是沒有變化的,或者說像素當量在橫軸方向上是幾乎不變的,也就是說,在圖二中每一條橫線上兩個孔之間的距離基本是保持不變的,比如說距離鏡頭最近的一條紅線上,每個孔之間的像素距離是近似不變的(事實上也確實基本不變);
(3)我需要求解在豎直方向上像素當量與距離的關系;
(4)我需要解算相機平面角度。
2.1 豎直像素當量與距離關系
豎直像素當量與距離的關系推演,應該從定焦鏡頭的焦距公式入手,式子中t代表像素當量。
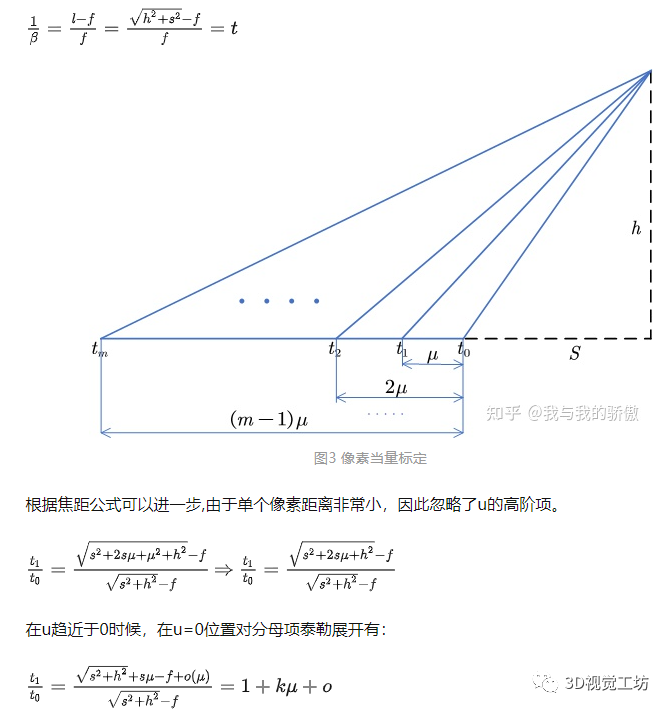
該式子表達了一個概念就是像素當量的比值是像素個數(shù)的線性遞增關系。那么對于視場內(nèi)任何一個位置的像素當量對最下測邊緣像素當量的比值應該有:
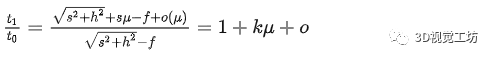
那么基于該公式就可以對底面坐標進行標定。圖2中將每一橫行的點連接在了一起,那么以最下測邊緣為底邊,前一條變距離最下測邊緣距離為視場標定前l(fā)cm,并且,該lcm由有限個像素m組成,那么對這連續(xù)的像素分點進行建模,構(gòu)建像元與實際尺寸之間的關系有:
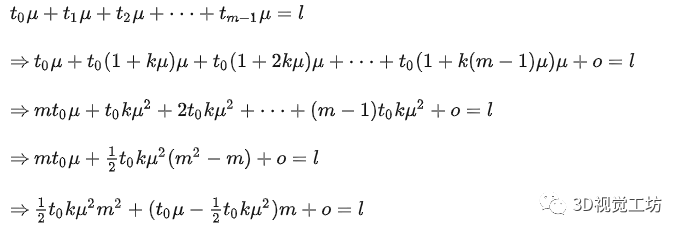
因此從上式可以反映出一個重要的推論,圖像上任何一點到基準線(圖2中最下測直線)的像素個數(shù)與實際距離間的關系為二次項關系。舉一個例子,在上圖2中一共有10條線,從上到下,第十條為基準線,第九條與第十條之間具有138個像素,此時真實距離為視角標定前的2.5cm;第八條與第十條之間具有138+125個像素,此時真實距離為視角標定前的5cm;第七條與第十條之間具有138+125+113個像素,此時真實距離為視角標定前的7.5cm。以此類推,就可以構(gòu)建相關函數(shù)。
此處埋下一個伏筆,對于該部分的像素當量與距離之間的關系有兩個需要注意的部分,一是我沒有直接把像素個數(shù)與2.5,5,7.5這幾個數(shù)直接擬合,因為這里面有一個視場角的問題,舉個例子,一個東西長10cm,但是你用斜著的視場去看的時候,這個東西肯定沒有10cm,這部分我會在下一部分中給出介紹;另一個伏筆,前面關系式子中m的二次項與一次項系數(shù)相加實際上就是基準線上的視場距離。
2.2 視場角解算
視場角解算是一個很有意思的問題。我不記得我在前一篇文章中是否解釋過這個問題,但是這里面確實就是這樣,一個物體在傾斜相機上的投影會導致距離發(fā)生改變,如圖3所示。
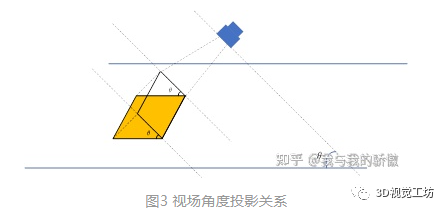
這也是我在2.1最后說的第一個伏筆,兩條線之間的2.5cm在投影到相機成像平面后不會再是2.5cm了,應該是其乘以視場角的余弦值。這也是為什么我不直接在2.1中給出直接擬合的原因。那么如何求解這個視場傾角呢?這里面我思考了很多,甚至一度想直接給固定值算了,但是我又覺得這很不靠譜,一定有什么辦法能夠推出視場角。后來,我想到了這個圖4。
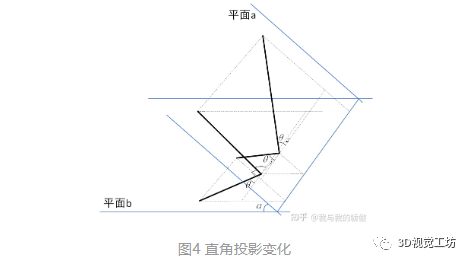
圖4中直角三角形在斜面投影過程中,直角三角形變成了鈍角三角形,究其原因是投影后平行于平面交線方向大小不變,垂直于交線方向變小,因此直角邊合投影的角度變大,兩條直角邊的角度都變大,導致投影后角度大于90°。因此,依靠立方體的角度變化可以反演投影面夾角。經(jīng)過分析發(fā)現(xiàn)一個問題, 如果直角的兩條邊分別垂直和平行于兩個平面的交線,那么直角角度并不發(fā)生改變,因此在圖4中有如下的關系:

因此在已知投影后與投影交線的夾角可以解算兩個平面夾角有:

tanθ1tanθ2=cos2α 2.3 橫向像素當量與數(shù)值距離關系
在理解橫向像素當量問題前先回憶一下2.1中的縱向像素當量問題,縱向像素當量隨著距離變化規(guī)律是一個二維函數(shù)規(guī)律,隨著目標點到基準線距離的變化,一個像素代表的實際距離呈規(guī)律性變化。在忽略了橫向畸變情況下,每一行的橫向當量也存在規(guī)律性變化。在給出基線上單個像素當量,與基線不同的距離得到的一維比例關系也應該符合與2.1中相同的一維線性公式。
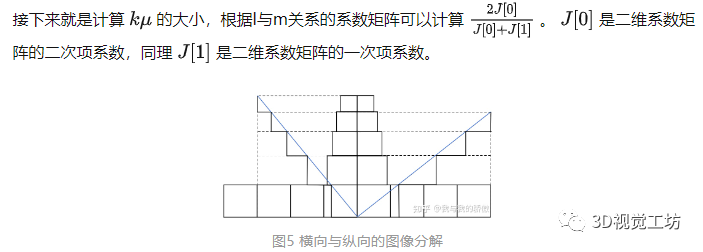
3、求解
在單目下的立方體被投影成一個六邊形。六邊形中三條邊為主要測量邊,其中兩條邊在標準平面上。

圖6 邊緣提取
標準平面上的兩條邊有以下兩個目的:
(1)根據(jù)夾角計算鏡頭成像夾角。標準直角在鏡頭投影后變成鈍角,利用2.2的視場解算方法可以得到鏡頭與平面夾角;
(2)將平面上兩條邊分別按照豎向與橫向進行分解,橫向與豎向上的分解結(jié)果根據(jù)像素數(shù)量分別代入2.1與2.2的系數(shù)公式計算真實長度。
圖2中背景底線將用于獲得二次項擬合系數(shù)矩陣。
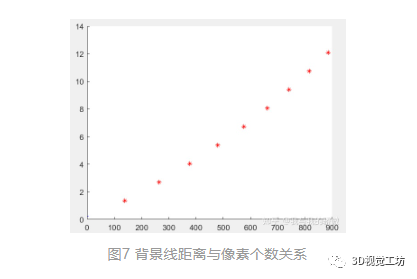
根據(jù)圖7獲取的系數(shù)矩陣有[6.63840796147980e-06,0.00750901860528093,0.215679358071086]。
利用系數(shù)矩陣代入可以獲取的長度為4.65009與6.36081。
最后是利用高度特征邊獲取高度的計算,高度的計算是一個逆向過程,圖3中從出發(fā)點到最遠點,鏡頭到點的距離越來越遠,當量越來越小;但是由于豎直高度原因,高度上的點,越向上反而離鏡頭越近,也就是此時的當量越來越大。與前文中的一次型相反,在高度的計算當量越來越大就可以實現(xiàn)高度的反演。
利用該方法獲取的高度為2.88764。
利用千分尺獲取的三條邊長度分別為4.6、6.4與2.8cm。
4、總結(jié)
做一個簡單的總結(jié)。
首次接觸該項目是一個在22年年初,大概3月份就完成了整體方案方法的設計,本想著早一些把利用單目方法獲取圖像計算體積的一次嘗試寫在知乎文章里,但是拖延癥一拖再拖到22年年底的圣誕節(jié)。
評價整體的方案方法來說,全文其實就提出了一個概念,就是利用泰勒展開消去高階項得到的像素當量與標準距離之間的二次項關系。其實方法來說科學性并不是非常足,尤其是利用該特點反推待測物高度時候,應該說,這是單目需要重點解決的問題之一,但是我在文中涉及到的方法有一些草率。
單目視覺到底有沒有應用價值呢?從需求來看,在給機場的箱體包裹計算、快遞的包裹大小計算上其實還是有意義的,而且在方便人工測量分揀上還是有價值的。
單純依靠單目視覺是無法處理深度問題的,雖然現(xiàn)在也設計推出了很多深度相機,但是深度相機的應用對象并不是對目標做三維反演。所以單目視覺需要搭配其他標準物來實現(xiàn)標定測量,而且這個標準物一定要出現(xiàn)在視場中,該文的光學平臺就是系統(tǒng)的標定物,這或許可以為單目視覺測量提供一種思路。
當前的標定與反演方法來說,還是要依靠漲勢標定法,張氏標定法具有非常高的普適性,但是在處理特殊問題上,確實可以用更多的方法實現(xiàn)標定的簡化,這也是我在全文中寫了這么多的目的。
最后,該項目來源于某校的本科畢業(yè)設計,根據(jù)畢業(yè)設計上的評語認為該方法在處理上具有特殊性,但是我采用同樣的程序跑了幾個差不多的立方體得到的數(shù)據(jù)結(jié)果還是蠻符合千分尺的測量結(jié)果,我個人會認為雖然方法草率了些,但是適用性,在光學平臺上放置立方體的測量結(jié)果我還是很認可的。
最后的最后,如果有人能認真閱讀,我真的會非常感謝各位的指正~!單目立體視覺完全是個人愛好,抽空拿出來做了一點算法的研究,如果有需要,相關利用Halcon完成的代碼完全可以開源。再拜謝。
審核編輯 :李倩
-
圖像
+關注
關注
2文章
1084瀏覽量
40455 -
單目視覺
+關注
關注
0文章
17瀏覽量
23598 -
工業(yè)相機
+關注
關注
5文章
322瀏覽量
23623
原文標題:【光電智造】單目立體視覺:我用單目相機求了個體積!
文章出處:【微信號:今日光電,微信公眾號:今日光電】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
雙目立體視覺原理大揭秘(二)
雙目立體視覺的運用
雙目立體視覺在嵌入式中有何應用
基于OpenCV的單目攝像機標定
遺傳算法的單目相機標定
基于雙目立體視覺的橋梁裂縫測量
雙相機立體視覺和結(jié)構(gòu)光立體視覺原理及優(yōu)勢對比
如何使用FPGA實現(xiàn)三目立體視覺外極線校正的方法
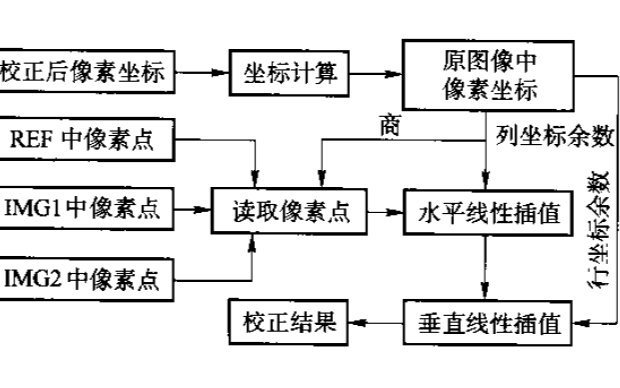
如何使用FPGA實現(xiàn)微型實時多目立體視覺機的設計
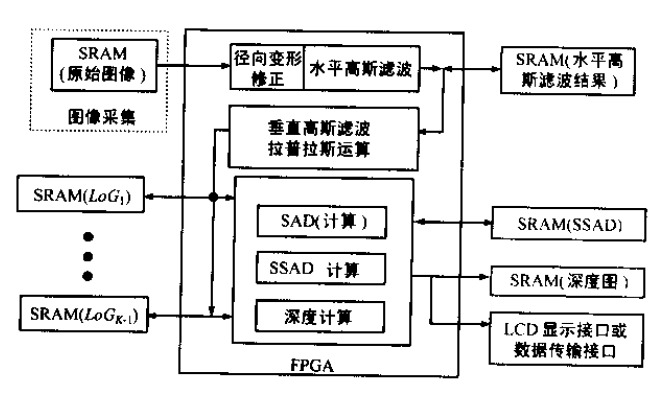
基于單目立體視覺的視覺測量步驟
密集單目SLAM的概率體積融合概述
雙目立體視覺是什么?單目視覺與雙目立體視覺的區(qū)別?
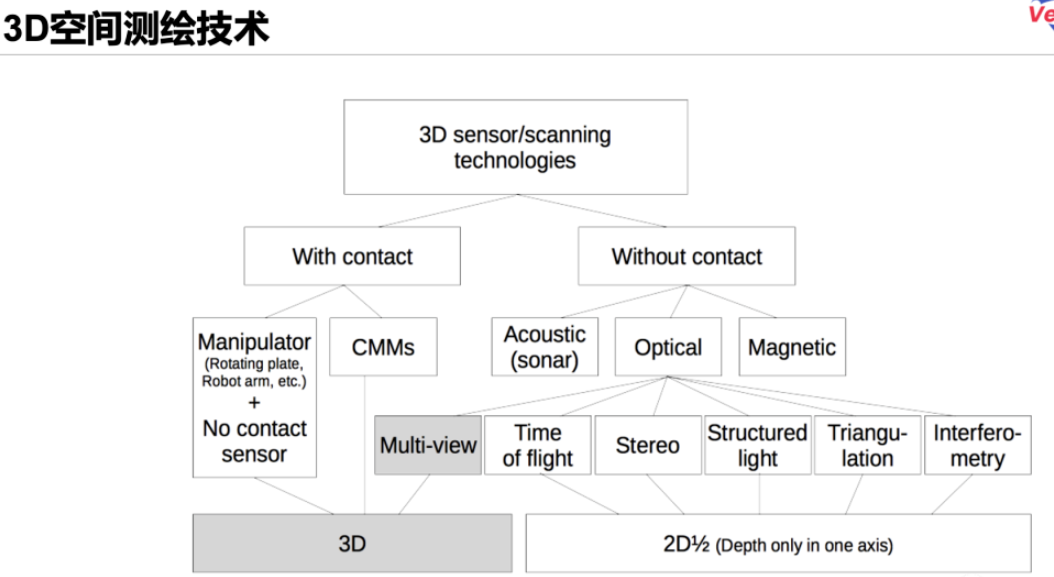




 單目立體視覺:我用單目相機求了個體積!
單目立體視覺:我用單目相機求了個體積!










評論