今天的題目是 53. Maximum Subarray 最大子序和
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
給定一個整數數組 nums ,找到一個具有最大和的連續子數組(子數組最少包含一個元素),返回其最大和。
示例:
輸入: [-2,1,-3,4,-1,2,1,-5,4],
輸出: 6
解釋: 連續子數組 [4,-1,2,1] 的和最大,為 6。
進階:
如果你已經實現復雜度為 O(n) 的解法,嘗試使用更為精妙的分治法求解。
Solutions:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
max_sum = nums[0]
lst = 0
# if(len(nums)==1): return nums[0]
'''
設置一個累加值,一個next_item值,一個max_sum值進行比較。
累加值是經過的數值累加的結果,next_item指示循環中的下一個新值,
max_sum用來保留全局最大,并做返回值。
'''
for next_item in nums:
lst = max(next_item,lst+next_item)
max_sum = max(max_sum,lst)
return max_sum
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
'''
用DP的思想來解,并對數組進行原地修改,修改后的值等于該位置之前的最大累加和。
nums[0]不變,從nums[1]開始更新,對于i位置新值等于nums[i]和nums[i]+累加值
nums[i-1]中最大項。如果nums[i]小于0則累加后數值變小,經過max之后會被篩選掉。
最后返回nums數組中的最大值即可。
'''
for i in range(1, len(nums)):
nums[i] = max(nums[i], nums[i] + nums[i - 1])
return max(nums)
-
元素
+關注
關注
0文章
47瀏覽量
8429 -
連續
+關注
關注
0文章
16瀏覽量
8851 -
數組
+關注
關注
1文章
417瀏覽量
25939
發布評論請先 登錄
相關推薦
請問數組定義全部是0,節點最大子節點數目是多少呢?
為什么架空輸電線路的零序電抗大于其正序電抗?
What is the maximum temperatur
什么是maximum DSL speeds
零序保護的最大特點是什么_零序保護特點詳解
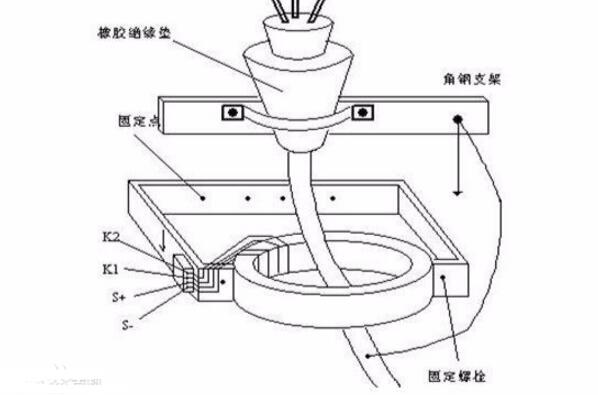
零序保護有方向性嗎_零序保護的最大特點




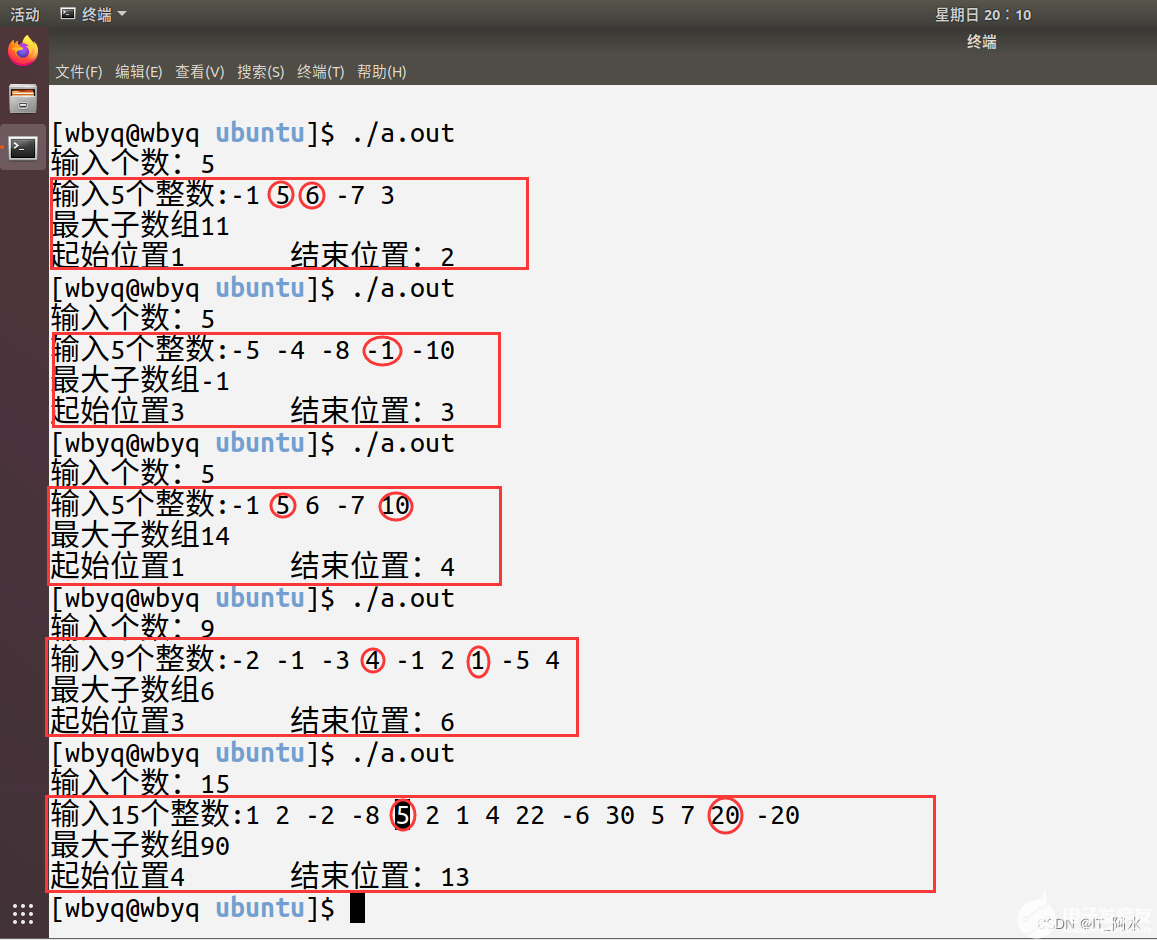
 Maximum Subarray 最大子序和
Maximum Subarray 最大子序和










評論