位操作(Bit Manipulation)可以有很多技巧,有一個叫做 Bit Twiddling Hacks 的網站收集了幾乎所有位操作的黑科技玩法
但是這些技巧大部分都過于晦澀,我覺得可以作為字典查閱,沒必要逐條深究。但我認為那些有趣的、有用的位運算技巧,是我們每個人需要掌握的。
所以本文由淺入深,先展示幾個有趣(但沒卵用)的位運算技巧,然后再匯總幾個在算法題以及工程開發中常用的位運算技巧。
幾個有趣的位操作
利用或操作`|`和空格將英文字符轉換為小寫
('a'|'')='a'
('A'|'')='a'
利用與操作`&`和下劃線將英文字符轉換為大寫
('b'&'_')='B'
('B'&'_')='B'
利用異或操作`^`和空格進行英文字符大小寫互換
('d'^'')='D'
('D'^'')='d'
以上操作能夠產生奇特效果的原因在于 ASCII 編碼。ASCII 字符其實就是數字,恰巧空格和下劃線對應的數字通過位運算就能改變大小寫。有興趣的讀者可以查 ASCII 碼表自己算算,本文就不展開講了。
不用臨時變量交換兩個數
inta=1,b=2; a^=b; b^=a; a^=b; //現在a=2,b=1
加一
intn=1; n=-~n; //現在n=2
減一
intn=2; n=~-n; //現在n=1
判斷兩個數是否異號
intx=-1,y=2; booleanf=((x^y)
如果說前 6 個技巧的用處不大,這第 7 個技巧還是比較實用的,利用的是補碼編碼的符號位。整數編碼最高位是符號位,負數的符號位是 1,非負數的符號位是 0,再借助異或的特性,可以判斷出兩個數字是否異號。
當然,如果不用位運算來判斷是否異號,需要使用 if else 分支,還挺麻煩的。你可能想利用乘積來判斷兩個數是否異號,但是這種處理方式容易造成整型溢出,從而出現錯誤。
index & (arr.length - 1) 的運用
我在單調棧解題套路中介紹過環形數組,其實就是利用求模(余數)的方式讓數組看起來頭尾相接形成一個環形,永遠都走不完:
int[]arr={1,2,3,4}; intindex=0; while(true){ //在環形數組中轉圈 print(arr[index%arr.length]); index++; } //輸出:1,2,3,4,1,2,3,4,1,2,3,4...
但模運算%對計算機來說其實是一個比較昂貴的操作,所以我們可以用&運算來求余數:
int[]arr={1,2,3,4}; intindex=0; while(true){ //在環形數組中轉圈 print(arr[index&(arr.length-1)]); index++; } //輸出:1,2,3,4,1,2,3,4,1,2,3,4...
簡單說,& (arr.length - 1)這個位運算能夠替代% arr.length的模運算,性能會更好一些。
那問題來了,現在是不斷地index++,你做到了循環遍歷。但如果不斷地index--,還能做到環形數組的效果嗎?
答案是,如果你使用%求模的方式,那么當index小于 0 之后求模的結果也會出現負數,你需要特殊處理。但通過&與運算的方式,index不會出現負數,依然可以正常工作:
int[]arr={1,2,3,4}; intindex=0; while(true){ //在環形數組中轉圈 print(arr[index&(arr.length-1)]); index--; } //輸出:1,4,3,2,1,4,3,2,1,4,3,2,1...
我們自己寫代碼一般用不到這個技巧,但在學習一些其他代碼庫時可能會經常看到,這里留個印象,到時候就不會懵逼了。
n & (n-1) 的運用
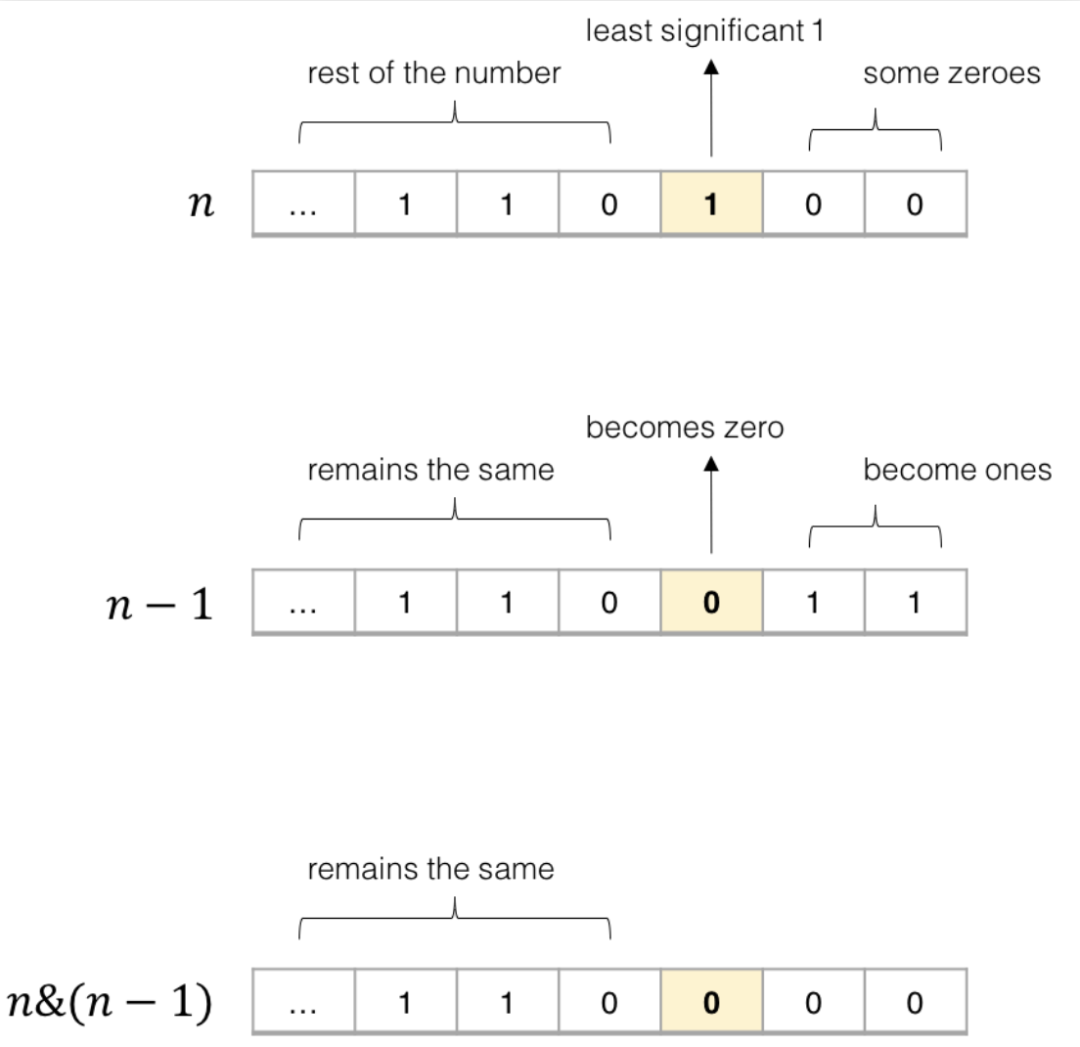
n & (n-1)這個操作在算法中比較常見,作用是消除數字n的二進制表示中的最后一個 1。
看個圖就很容易理解了:
其核心邏輯就是,n - 1一定可以消除最后一個 1,同時把其后的 0 都變成 1,這樣再和n做一次&運算,就可以僅僅把最后一個 1 變成 0 了。
1、計算漢明權重(Hamming Weight)
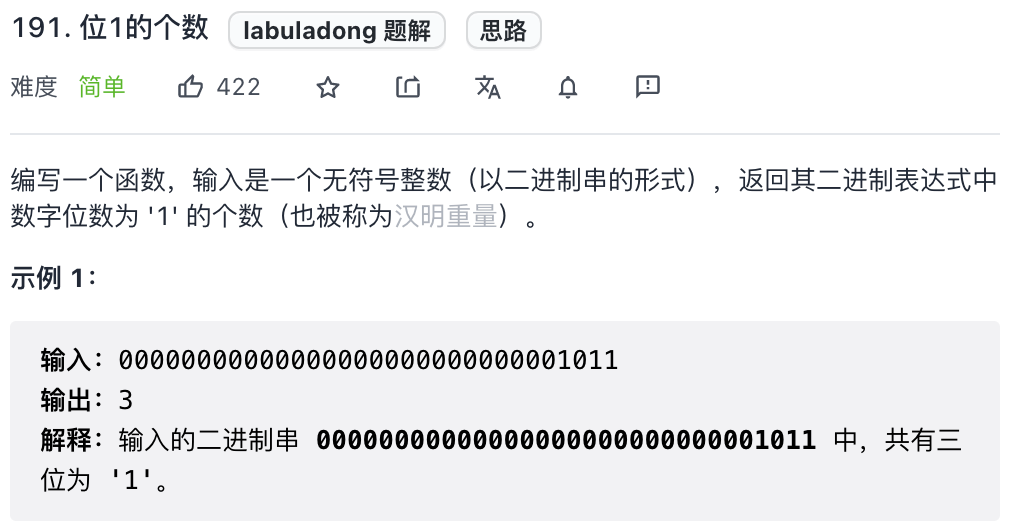
這是力扣第 191 題「位 1 的個數」:
就是讓你返回n的二進制表示中有幾個 1。因為n & (n - 1)可以消除最后一個 1,所以可以用一個循環不停地消除 1 同時計數,直到n變成 0 為止。
inthammingWeight(intn){ intres=0; while(n!=0){ n=n&(n-1); res++; } returnres; }
2、判斷一個數是不是 2 的指數
力扣第 231 題「2 的冪」就是這個問題。
一個數如果是 2 的指數,那么它的二進制表示一定只含有一個 1:
2^0=1=0b0001 2^1=2=0b0010 2^2=4=0b0100
如果使用n & (n-1)的技巧就很簡單了(注意運算符優先級,括號不可以省略):
booleanisPowerOfTwo(intn){ if(n<=?0)?return?false; ????return?(n?&?(n?-?1))?==?0; }
a ^ a = 0 的運用
異或運算的性質是需要我們牢記的:
一個數和它本身做異或運算結果為 0,即a ^ a = 0;一個數和 0 做異或運算的結果為它本身,即a ^ 0 = a。
1、查找只出現一次的元素
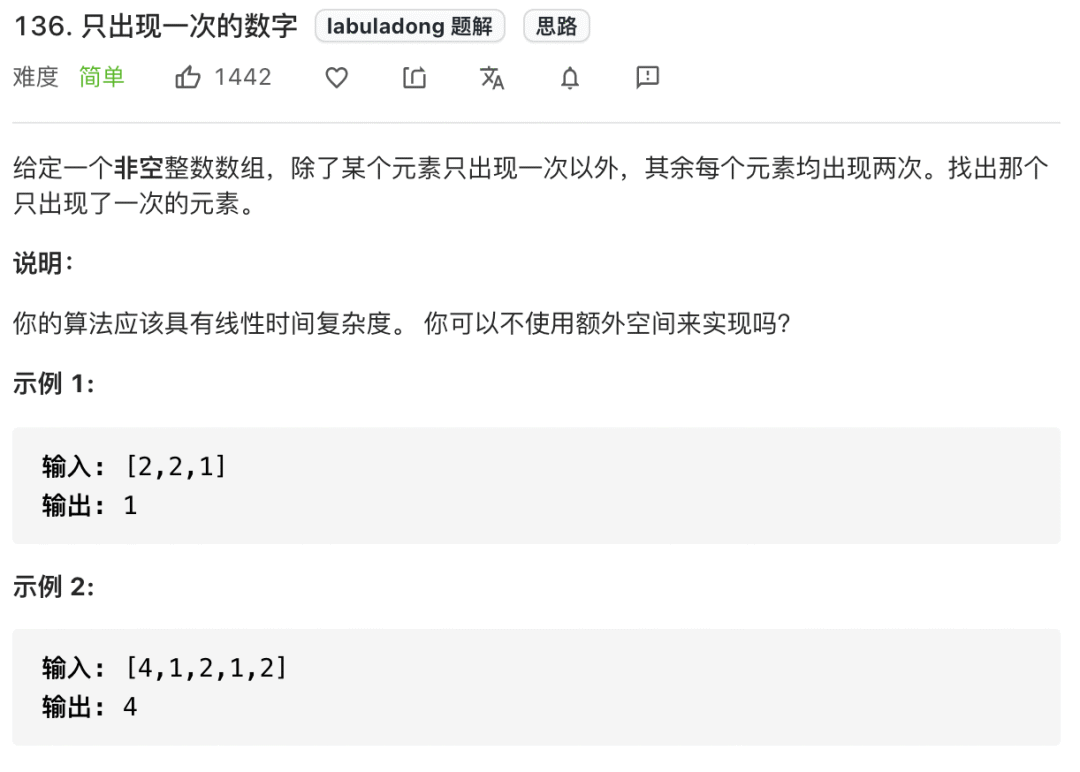
這是力扣第 136 題「只出現一次的數字」:
對于這道題目,我們只要把所有數字進行異或,成對兒的數字就會變成 0,落單的數字和 0 做異或還是它本身,所以最后異或的結果就是只出現一次的元素:
intsingleNumber(int[]nums){ intres=0; for(intn:nums){ res^=n; } returnres; }
2、尋找缺失的元素
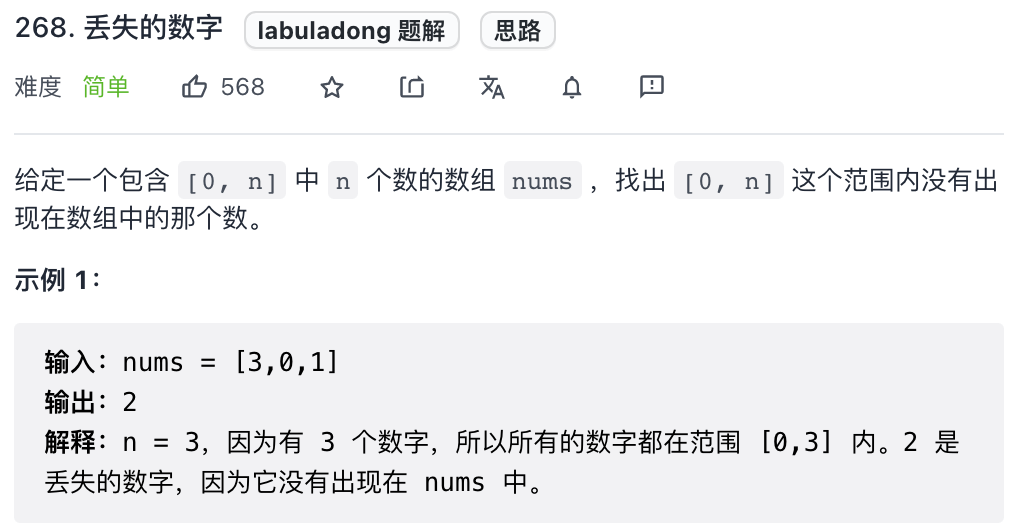
這是力扣第 268 題「丟失的數字」:
給一個長度為n的數組,其索引應該在[0,n),但是現在你要裝進去n + 1個元素[0,n],那么肯定有一個元素裝不下嘛,請你找出這個缺失的元素。
這道題不難的,我們應該很容易想到,把這個數組排個序,然后遍歷一遍,不就很容易找到缺失的那個元素了嗎?
或者說,借助數據結構的特性,用一個 HashSet 把數組里出現的數字都儲存下來,再遍歷[0,n]之間的數字,去 HashSet 中查詢,也可以很容易查出那個缺失的元素。
排序解法的時間復雜度是 O(NlogN),HashSet 的解法時間復雜度是 O(N),但是還需要 O(N) 的空間復雜度存儲 HashSet。
這個問題其實還有一個特別簡單的解法:等差數列求和公式。
題目的意思可以這樣理解:現在有個等差數列0, 1, 2,..., n,其中少了某一個數字,請你把它找出來。那這個數字不就是sum(0,1,..n) - sum(nums)嘛?
intmissingNumber(int[]nums){ intn=nums.length; //雖然題目給的數據范圍不大,但嚴謹起見,用long類型防止整型溢出 //求和公式:(首項+末項)*項數/ 2 longexpect=(0+n)*(n+1)/2; longsum=0; for(intx:nums){ sum+=x; } return(int)(expect-sum); }
不過,本文的主題是位運算,我們來講講如何利用位運算技巧來解決這道題。
再回顧一下異或運算的性質:一個數和它本身做異或運算結果為 0,一個數和 0 做異或運算還是它本身。
而且異或運算滿足交換律和結合律,也就是說:
2^3^2=3^(2^2)=3^0=3
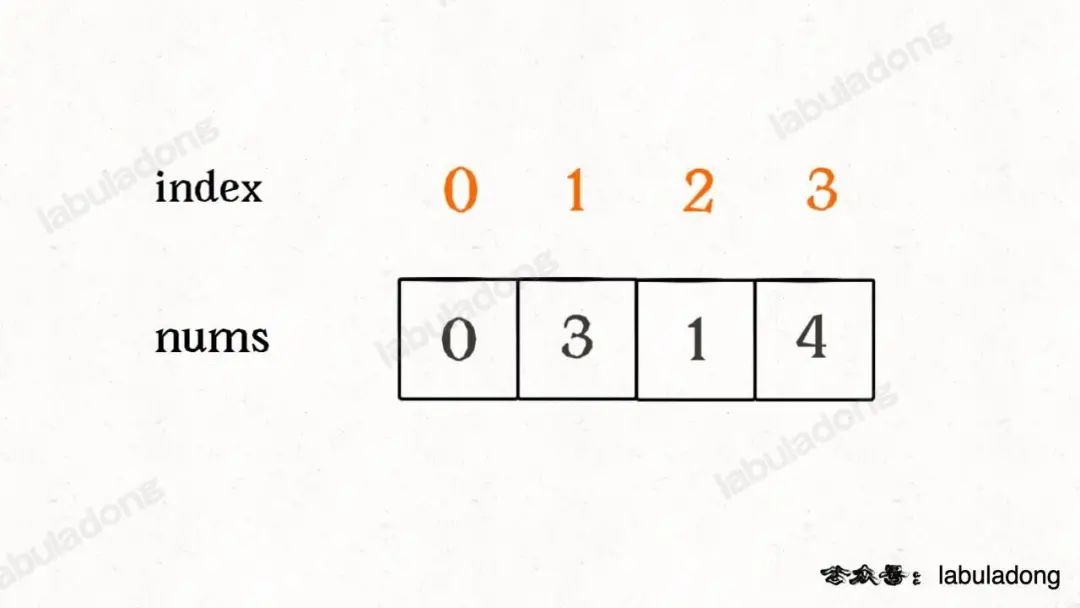
而這道題索就可以通過這些性質巧妙算出缺失的那個元素,比如說nums = [0,3,1,4]:
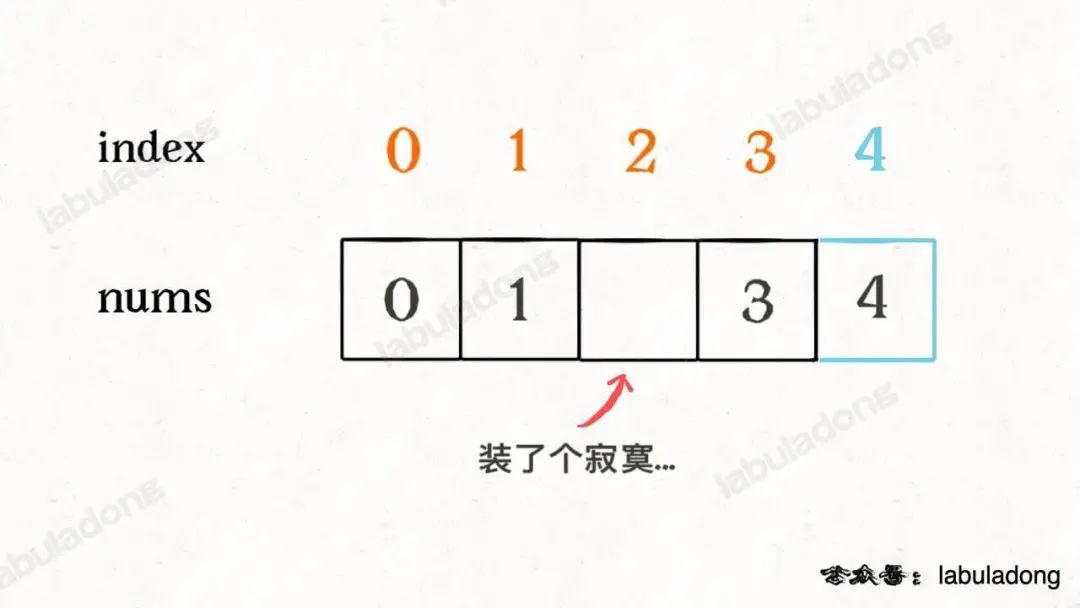
為了容易理解,我們假設先把索引補一位,然后讓每個元素和自己相等的索引相對應:
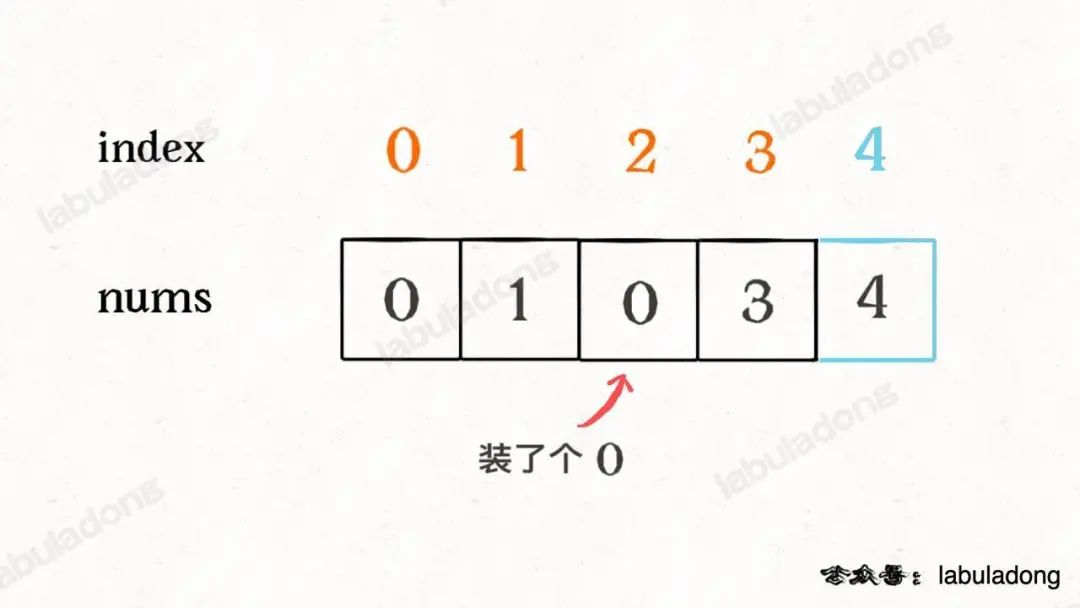
這樣做了之后,就可以發現除了缺失元素之外,所有的索引和元素都組成一對兒了,現在如果把這個落單的索引 2 找出來,也就找到了缺失的那個元素。
如何找這個落單的數字呢,只要把所有的元素和索引做異或運算,成對兒的數字都會消為 0,只有這個落單的元素會剩下,也就達到了我們的目的:
intmissingNumber(int[]nums){ intn=nums.length; intres=0; //先和新補的索引異或一下 res^=n; //和其他的元素、索引做異或 for(inti=0;i
由于異或運算滿足交換律和結合律,所以總是能把成對兒的數字消去,留下缺失的那個元素。
到這里,常見的位運算差不多都講完了。這些技巧就是會者不難難者不會,也不需要死記硬背,只要有個印象就完全夠用了。
審核編輯:劉清
-
計算機
+關注
關注
19文章
7508瀏覽量
88070 -
ASCII
+關注
關注
5文章
172瀏覽量
35121 -
Hash算法
+關注
關注
0文章
43瀏覽量
7383
原文標題:必知必會位運算技巧手冊
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 匯總幾個在算法題以及工程開發中常用的位運算技巧
匯總幾個在算法題以及工程開發中常用的位運算技巧











評論