LTI連續(xù)系統(tǒng)的響應(yīng)
連續(xù)系統(tǒng)的描述:電路圖建立微分方程
1.數(shù)學(xué)模型
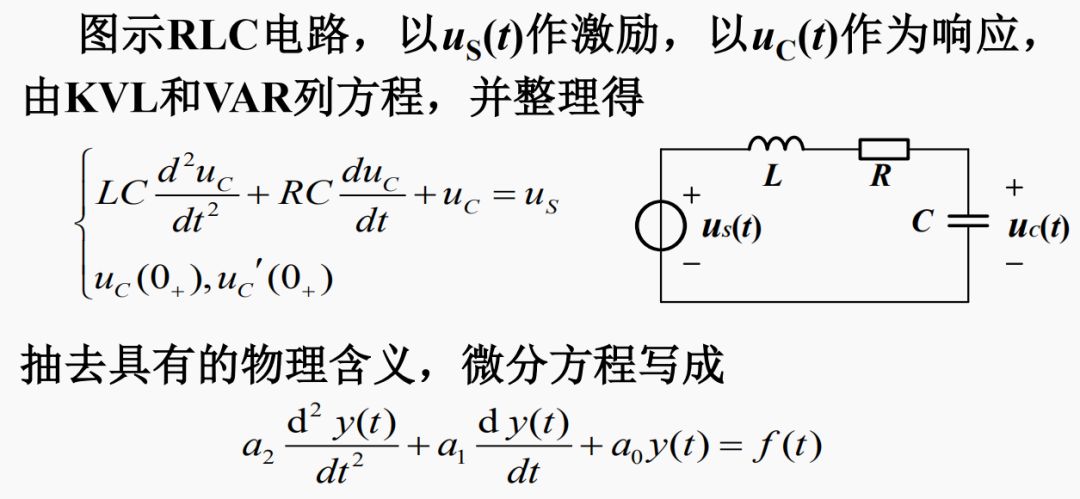
二階常系數(shù)線性微分方程
2.相似系統(tǒng)
相似系統(tǒng):能用相同方程描述的系統(tǒng)

微分方程的模擬框圖
基本部件:
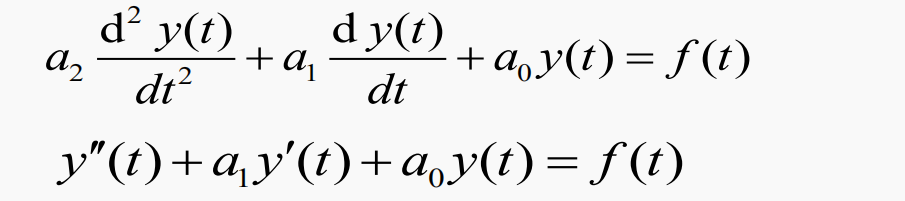
基本運(yùn)算:數(shù)乘、微分、相加
基本部件:加法器、數(shù)乘器、積分器
積分器的抗干擾性比微分器好(用積分器代替微分器)
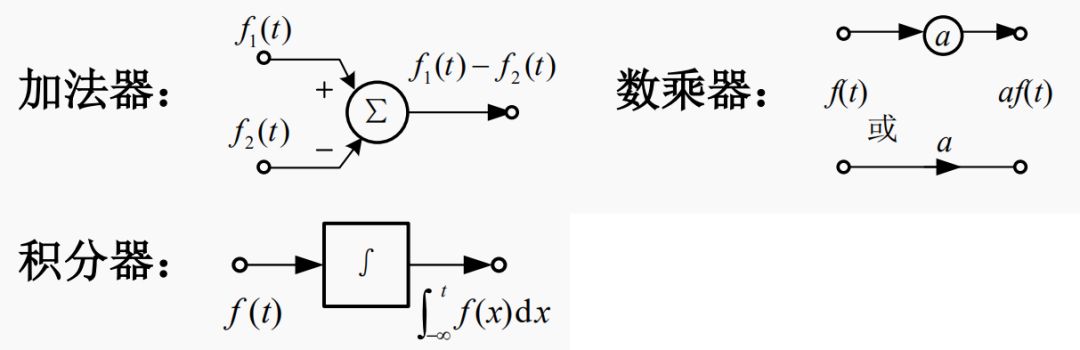
2.模擬框圖
模擬框圖:將微分方程用基本部件的相互聯(lián)接表征出來(lái)的圖,簡(jiǎn)稱框圖。
例1 已知y’’(t) + ay’(t)+ by(t) = f(t),畫(huà)出框圖。
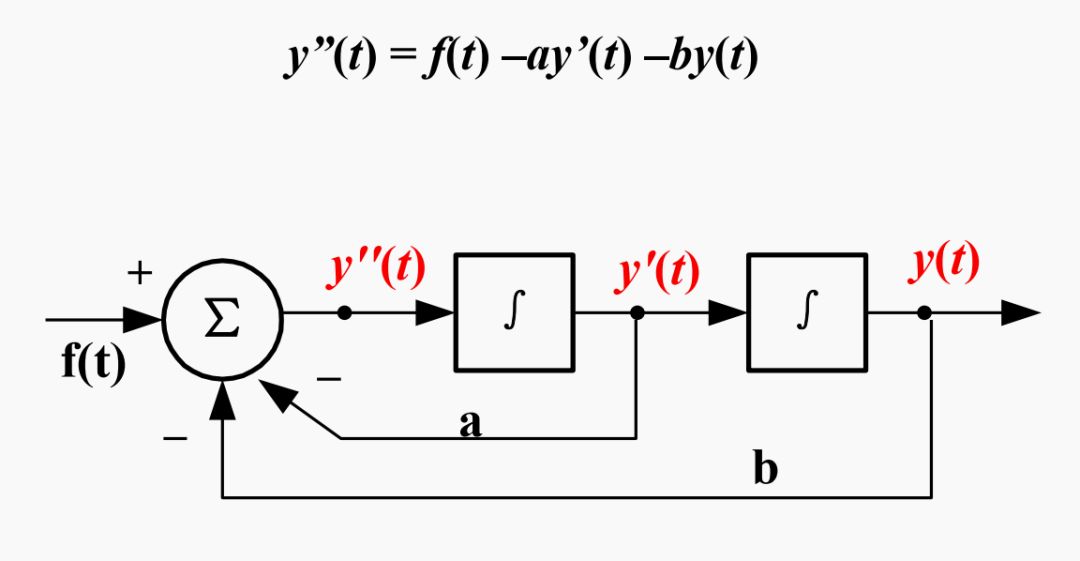
解:將方程改寫(xiě)為 y”(t) = f(t) –ay’(t) –by(t)
繪制步驟為:
(1)畫(huà)出兩個(gè)積分器;
(2)以最后一個(gè)積分器的輸出端為y(t);
(3)左邊第一個(gè)積分器的輸入端就是y”(t),也是加法器的輸出。
例2 已知y“(t) + 3y'(t)+ 2y(t) = 4f'(t) + f(t),畫(huà)框圖。
解:該方程右端含f(t)的導(dǎo)數(shù),引入輔助函數(shù)畫(huà)出框圖。 設(shè)輔助函數(shù)x(t)滿足
x“(t) + 3x'(t)+ 2x(t) = f(t)
移項(xiàng)整理得: x”(t) = -3x’(t)-2x(t) + f(t)
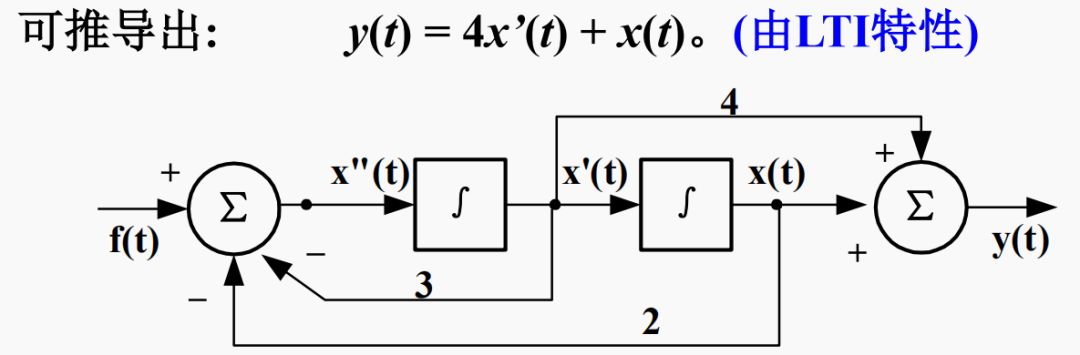
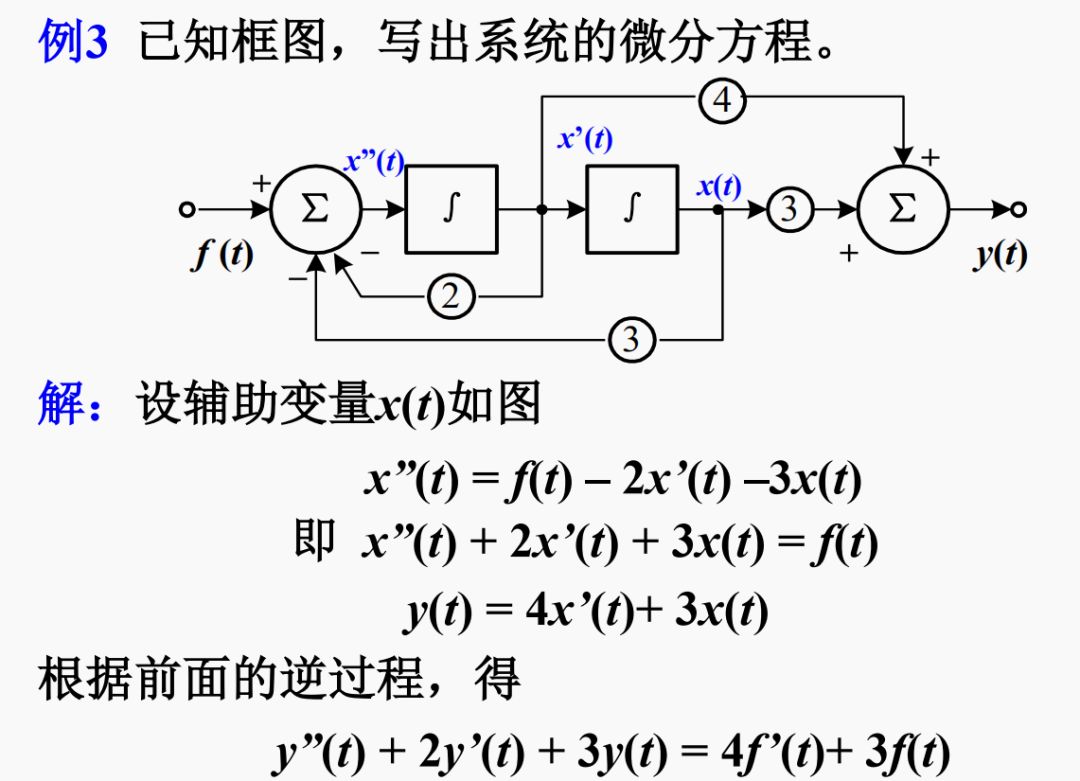
根據(jù)求和器列方程
微分方程的經(jīng)典解法
經(jīng)典解
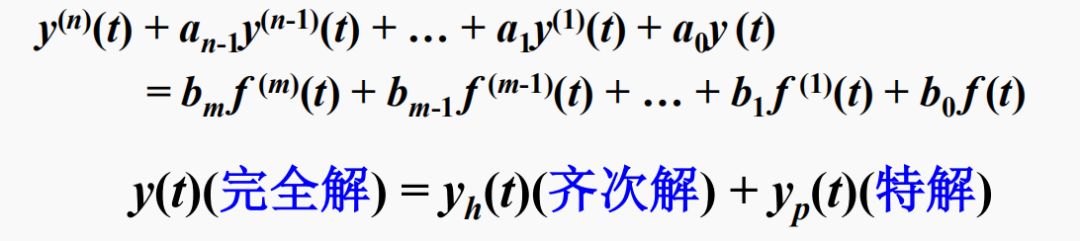
齊次解是對(duì)應(yīng)齊次微分方程的解:
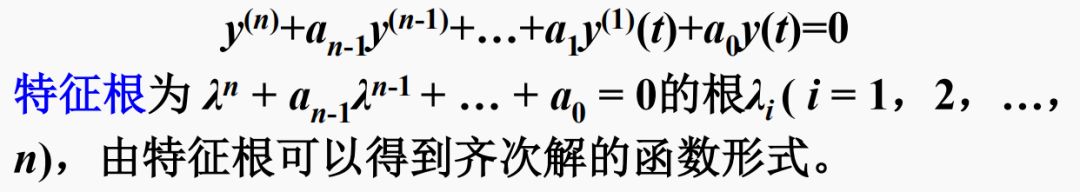
特解的函數(shù)形式與激勵(lì)的函數(shù)形式有關(guān)。
2.齊次解的常用函數(shù)形式
不同特征根所對(duì)應(yīng)的齊次解
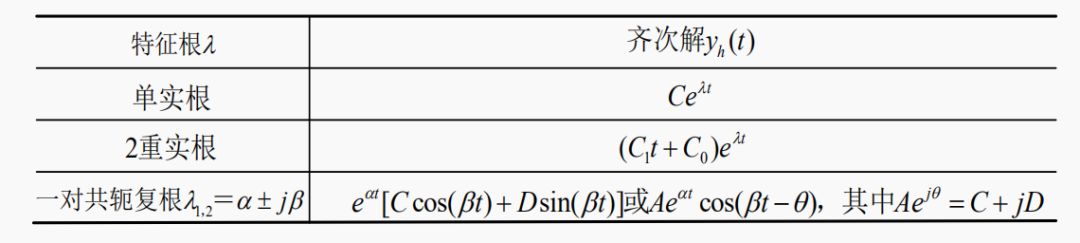
3.特解的常用函數(shù)形式
不同激勵(lì)所對(duì)應(yīng)的特解
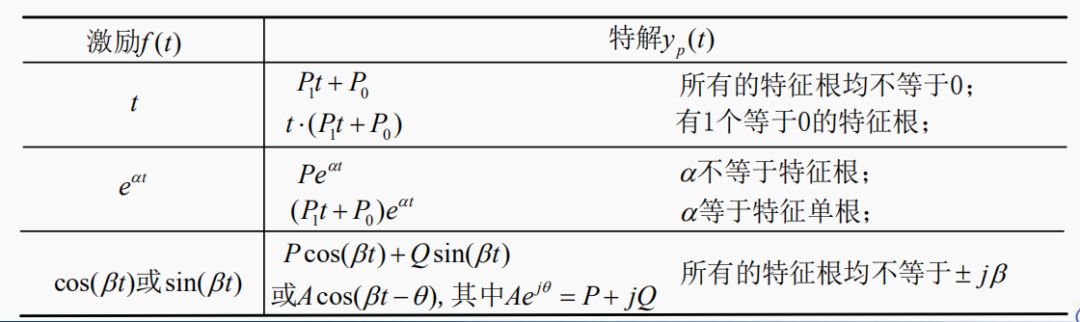


上式第一項(xiàng)系數(shù)C1 + Q0= 2,不能區(qū)分C1和Q0。
連續(xù)系統(tǒng)的初始值



結(jié)論:微分方程等號(hào)右端含有δ(t)時(shí),僅在等號(hào)左端y(t)的最高階導(dǎo)數(shù)中含有δ(t),則y(t)的次高階躍變,其余連續(xù); 若右端不含沖激函數(shù),則不會(huì)躍變。
零輸入響應(yīng)

求解步驟
(1)設(shè)定齊次解;
(2)代入初始值,求待定系數(shù)

零狀態(tài)響應(yīng)

求解步驟
(1)設(shè)定齊次解;
(2)設(shè)定特解,代入方程求解;
(3)代入初始值,求待定系數(shù)。


響應(yīng)分類
固有響應(yīng)和強(qiáng)迫響應(yīng)
固有響應(yīng)僅與系統(tǒng)本身的特性有關(guān),而與激勵(lì)的函數(shù)形式無(wú)關(guān)。
齊次解的函數(shù)形式僅與特征方程的根有關(guān),特征方程的根稱為系統(tǒng)的“固有頻率”,齊次解常稱為系統(tǒng)的固有響應(yīng)或自由響應(yīng)。
強(qiáng)迫響應(yīng)與激勵(lì)的函數(shù)形式有關(guān)。
特解的函數(shù)形式與激勵(lì)的函數(shù)形式有關(guān),常稱為強(qiáng)迫響應(yīng)。
暫態(tài)響應(yīng)和穩(wěn)態(tài)響應(yīng)
暫態(tài)響應(yīng)是指響應(yīng)中暫時(shí)出現(xiàn)的分量,隨著時(shí)間的增長(zhǎng),它將消失。
穩(wěn)態(tài)響應(yīng)是穩(wěn)定的分量,若存在,通常表現(xiàn)為階躍函數(shù)和周期函數(shù)。 比如,電路系統(tǒng)中的直流穩(wěn)態(tài)響應(yīng)和正弦穩(wěn)態(tài)響應(yīng)。


Matlab求解系統(tǒng)的響應(yīng)
求LTI系統(tǒng)的零狀態(tài)響應(yīng)的函數(shù)lsim,其調(diào)用格式為:
y=lsim(sys, f, t)
式中,t表示計(jì)算系統(tǒng)響應(yīng)的抽樣點(diǎn)向量; f是系統(tǒng)輸入信號(hào),sys是LTI系統(tǒng)模型,用來(lái)表示微分方程。
系統(tǒng)模型sys要借助tf函數(shù)獲得,其調(diào)用方式為:
sys=tf(b, a)
式中,b和a分別為微分方程的右端和左端各項(xiàng)的系數(shù)。 比如:
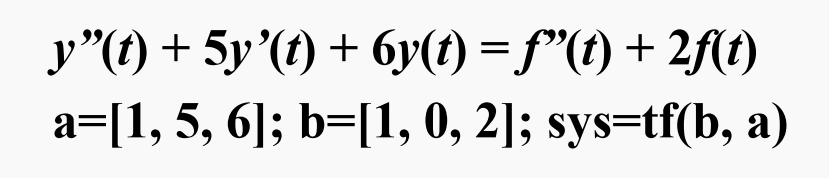
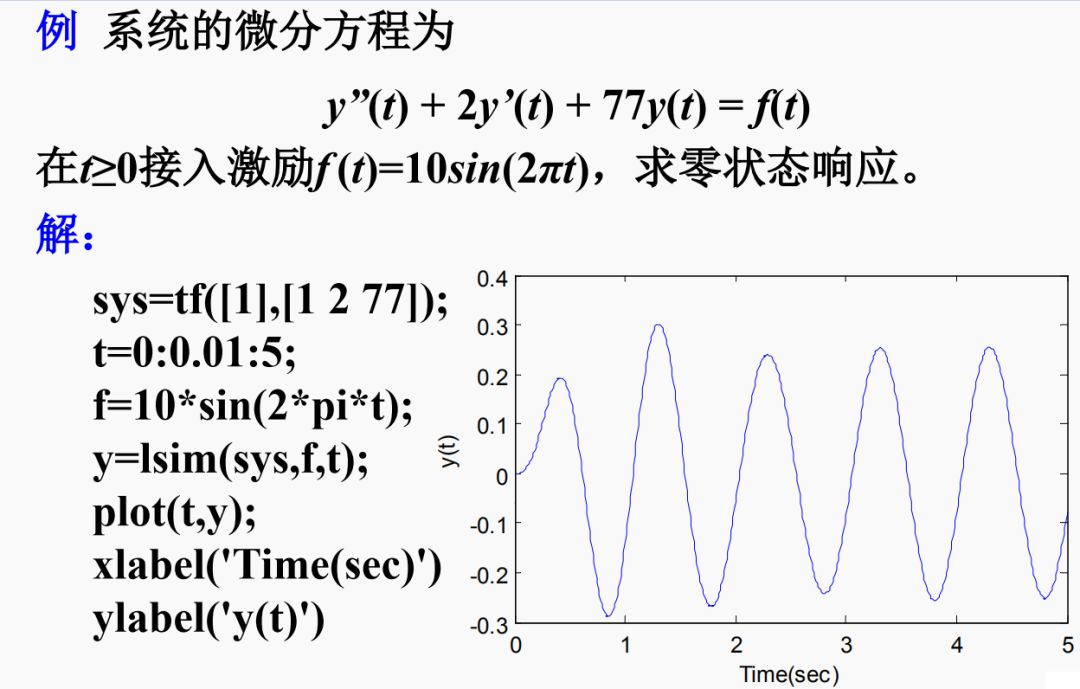
-
電路圖
+關(guān)注
關(guān)注
10365文章
10726瀏覽量
534967 -
響應(yīng)
+關(guān)注
關(guān)注
0文章
18瀏覽量
10881 -
數(shù)學(xué)模型
+關(guān)注
關(guān)注
0文章
83瀏覽量
12024 -
LTI
+關(guān)注
關(guān)注
0文章
11瀏覽量
10516 -
連續(xù)系統(tǒng)
+關(guān)注
關(guān)注
0文章
4瀏覽量
6768
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦

#硬聲創(chuàng)作季 #信號(hào)與系統(tǒng): LTI連續(xù)系統(tǒng)的響應(yīng)

[3.4.1]--連續(xù)時(shí)間LTI系統(tǒng)的沖激響應(yīng)

[3.7.1]--連續(xù)時(shí)間LTI系統(tǒng)響應(yīng)求解舉例
連續(xù)時(shí)間LTI系統(tǒng)狀態(tài)方程的建立
連續(xù)時(shí)間LTI系統(tǒng)狀態(tài)方程的求解
連續(xù)時(shí)間LTI系統(tǒng)的復(fù)頻域分析.ppt
連續(xù)時(shí)間LTI系統(tǒng)的系統(tǒng)函數(shù).ppt
連續(xù)時(shí)間LTI系統(tǒng)的穩(wěn)定性.ppt
LTI系統(tǒng)對(duì)輸入的響應(yīng)
AMBA LTI協(xié)議規(guī)范
連續(xù)時(shí)間LTI系統(tǒng)的復(fù)頻域分析視頻教程
連續(xù)時(shí)間LTI系統(tǒng)的頻率響應(yīng).ppt
連續(xù)時(shí)間LTI系統(tǒng)的頻域分析
連續(xù)信號(hào)與系統(tǒng)的頻域分析資料和方法,信號(hào)與系統(tǒng)三電子課件免費(fèi)下載
LTI系統(tǒng)的單位階躍響應(yīng)詳細(xì)資料說(shuō)明





 LTI連續(xù)系統(tǒng)的響應(yīng)
LTI連續(xù)系統(tǒng)的響應(yīng)










評(píng)論