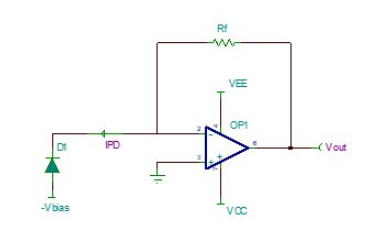
在測試測量和醫療行業中,許多應用采集的原始信號都是光信號,例如LiDAR,OTDR,PCR等。在采集的過程中這類應用會不可避免的進行光電轉換,首先通過光電二極管把光信號轉化成電流信號,然后在通過跨阻放大電路把電流信號轉成電壓信號,之后再進行信號調理,最終輸入ADC中。
其中跨阻放大電路的設計尤為關鍵,主要包括兩方面,一方面是穩定性設計,一方面是噪聲控制。接下來我們主要介紹如何借助TINA-TI來進行跨阻放大電路的穩定性設計。
一、 跨阻放大電路介紹
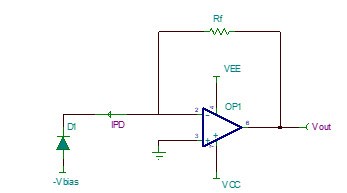
圖 1 理想的跨阻放大電路
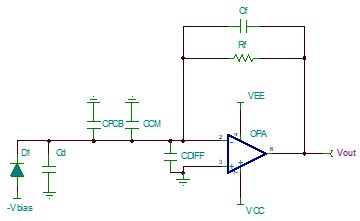
圖 2 實際的跨阻放大電路
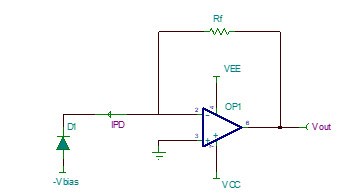
如圖1所示,是理想的跨阻放大器電路,其工作原理如公式(1)所示。

但是在實際應用中,光電二極管會有一個從1pF至上百pF之間的寄生電容Cd。運算放大器的輸入共模Ccm和輸入差模電容Cdiff也需要考慮。除此之外,還有PCB的寄生電容Cpcb。
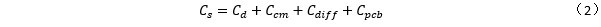
這時需要在反饋回路上加入反饋電容Cf,來對環路進行補償。如圖2所示。
最終可以等效為:
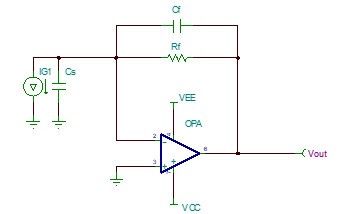
圖 3 等效電路圖
二、設計及仿真過程
仿真工具:TINA-TI。
在開始設計之前,我們要清楚Rf和Cs應該是已知的。
一般來講,設計思路無外乎以下兩種。
1)需要根據我們對跨阻放大電路的目標閉環帶寬f-3dB去選出合適的GBP的運放和反饋電容Cf。
2)根據所選運算放大器的GBP,計算跨阻放大電路可以實現的閉環帶寬f-3dB和反饋電容Cf。
為了便于理解,以一個開環增益為120dB,主極點為1kHZ運放為例,先從理想情況出發,逐步貼近實際情況。
1.理想的跨阻放大電路的穩定性分析
圖 4 理想的跨阻放大電路
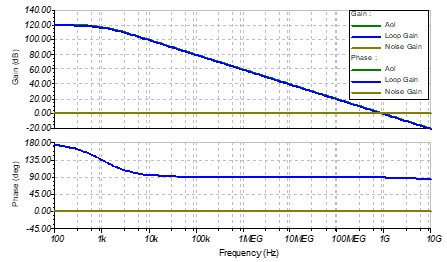
圖 5 理想跨阻放大電路的伯德圖
從伯德圖,我們可以看出來,該運放的開環增益曲線Aol在1KHz處有一個主極點,使得Loop Gain以-20dB/dec速度下降,并在1GHz處穿越0dB,同時該主極點使Loop Gain的相位裕度等于90°,滿足運放電路的穩定性判據,所以該系統處于穩定狀態。
在對理想跨阻放大器的穩定性進行分析之后,讓我們進一步考慮實際情況,把PD的結電容和運放的輸入電容考慮進來。
2. Cs對跨阻放大電路的穩定性影響
我們假設全部的輸入電容Cs=10pF,目標的跨阻增益是Rf=159.15K?。
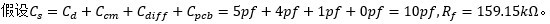
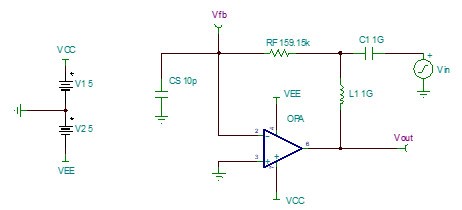
圖 6 考慮Cs的跨阻放大電路
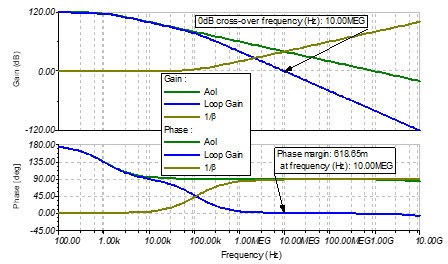
圖 7 考慮Cs的跨阻放大電路的伯德圖
首先觀察一下幅頻曲線:
噪聲增益1?β即閉環增益隨頻率的變化。
在低頻部分,10pF電容的阻抗非常大,可以認為是開路,運放會跟之前一樣作為一個單位增益的同相放大電路,所以它的幅值為0dB.
隨著頻率的上升,輸入電容Cs的阻抗開始下降,在100KHz處,Rf和Cs制造了一個零點1?(2π?159.15k??10pF)=100KHz。噪聲增益1?β將會以20dB/dec的速度上升。
從環路增益Loop Gain的角度出發,等價于開環增益Aol和噪聲增益1?β相減,將會在環路增益Loop Gain中出現兩個極點,等于0dB的點就是Loop Gain的穿越頻率點。最終Loop Gain會以-40dB/dec的斜率穿越0dB,根據自動控制理論,那該電路將會處于不穩定的狀態。
從相頻曲線上看:
在環路增益Loop Gain 曲線上,1KHz處的主極點會帶來〖90〗^°的相移,從100Hz處開始,在10KHz處完成相移。因為在100KHz處還有一個極點,相位會繼續下降,從10KHz開始,并在1MHz處完成相移,所以在穿越頻率點10MHz的相位裕度將會是0^°,根據自動控制理論,該電路將會處于不穩定的狀態。
為了避免這種不穩定的狀態,需要在反饋回路中加入一個反饋電容,所以接下來看一下引入反饋電容后,環路的穩定性將會發生什么樣的變化。
3. Cf對跨阻放大器電路的穩定性影響
先假設反饋回路上并聯了一個141fF的電容,后續會介紹如何計算反饋電容的容值。
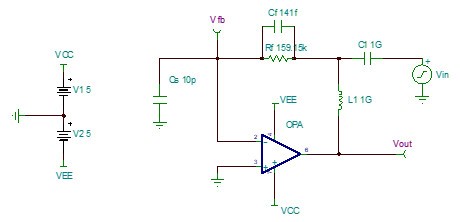
圖 8 加入Cf后的跨阻放大電路
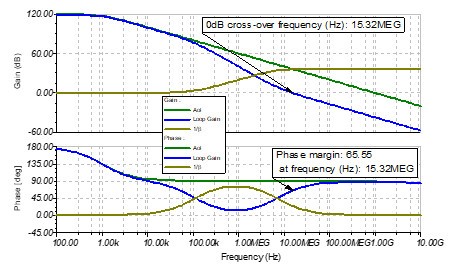
圖 9 加入Cf后跨阻放大電路的伯德圖
首先觀察一下幅頻曲線:
噪聲增益1?β在低頻部分,因為反饋電容Cf比輸入電容Cs小很多,它不會影響由Rf和Cs產生的零點的位置。在高頻部分,因為反饋電容Cf和反饋電阻Rf是并聯關系,所以在高頻部分反饋電阻Rf不再影響噪聲增益,最終的噪聲增益1?β由Cf和Cs決定,所以噪聲增益1?β的幅度將不再變化。也就是說,在噪聲增益的幅頻曲線中引入了一個由Rf和Cf產生的極點,頻率是1?(2π?159.15k??141) fF=7.09MHz。
對于環路增益Loop Gain而言,R_f和C_f在Loop Gain在7.09MHz處引入了一個零點,所以反饋電容Cf的作用是與Rf構成零點,恢復環路增益Loop Gain曲線中的相位裕度。如圖9所示,環路增益Loop Gain和噪聲增益1?β交叉發生在15.32MHz,由于該零點的存在,從該零點頻率的十分之一處700kHz開始,以45°/dec的速度增加。所以在環路增益的穿越頻率15.32MHz處,環路增益Loop Gain恢復了足夠的相位,從而獲得了約65°的相位裕量。
將反饋電容Cf設置為遠小于此141 fF的值將使Loop Gain中Rf和Cf形成的零點頻率提高。例如當Cf=14.1fF時,從相頻曲線上看,相位裕度低于理想值。
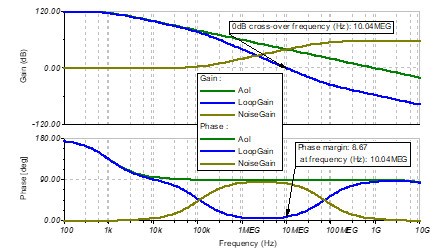
圖 10 Cf=14.1fF 的伯德圖
如果設置反饋電容Cf等于Cs,在噪聲增益中,Cf和Rf形成的極點頻率會接近于Cs和Rf形成的零點頻率,這會使相位裕度接近于90°,如圖11所示,最終導致系統的響應速度變慢。這里大家是否會有疑問,既然已經設置反饋電容Cf等于Cs了,那么為什么Cf和Rf形成的極點頻率與Cs和Rf形成的零點頻率不相等呢?
這是因為,噪聲增益中的這個零點,是由Cs,Cf和Rf共同形成的,只不過當Cf遠小于Cs時,我們可以把Cf忽略掉。
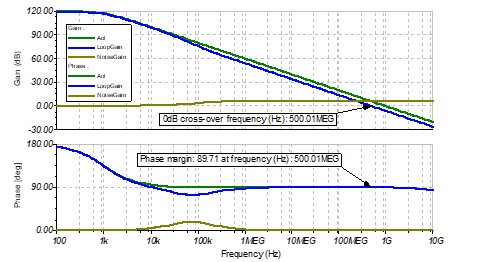
圖 11 Cf=Cs時的伯德圖
當設置Cf=70fF,141fF,280fF時,伯德圖如下:
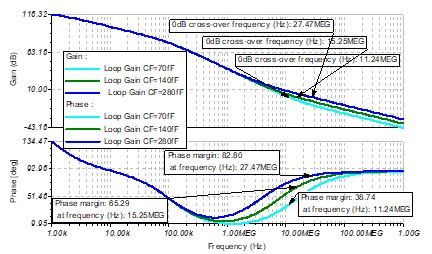
圖 12 Cf=70fF,141fF,280fF的伯德圖
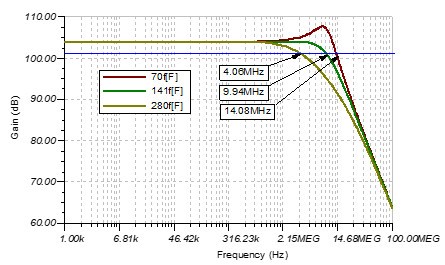
圖 13 Cf=70fF,141fF,280fF的閉環傳函的幅頻曲線
可以看到,隨著反饋電容Cf的增加,Loop Gain的穿越頻率越來越高,相位裕度越來越高,閉環帶寬越來越小。從閉環傳遞函數的角度上分析,反饋電容越大,Q越小,阻尼系數越大。與欠阻尼況和過阻尼相比,在臨界阻尼情況下(Q=0.707),系統從受擾動以后,趨近平衡所需的時間最短。通過改變反饋電容的大小,可以改變相位裕度來控制脈沖響應或者改變閉環增益。
4. 設計流程總結
1)確定Cs,反饋電阻Rf,閉環帶寬f-3dB。
例如,Cs=10fF,Rf=159.15 k?,f-3dB=10MHz
2)如果想得到巴特沃斯響應Q=0.707,根據公式(3),確定所需要的最小的GBP,根據結算結果,選擇帶寬合適的運放。

(3)
上面的公式是從何而來呢?可以參考一下《Transimpedance Considerations for High-Speed Amplifiers》,TIA電路的閉環傳遞函數是一個典型的二階振蕩環節,在獲得巴特沃斯響應時,品質因數Q=0.707時,諧振頻率fo=f-3dB。當根據TIA電路的閉環傳遞函數把fo的表達式寫出來的時候發現,該頻率點對應的是開環增益曲線和噪聲增益曲線沿第一個零點過后延長線的交點。
需要注意的是,如果選擇的運放的GBP比計算值大,那么在電路中計算時要按實際選擇運放的GBP計算實際的閉環帶寬。代入Cs=10fF,Rf=159.15 k?,f-3dB=10MHz,得:
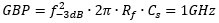
3)確定Cf。
同樣的,參考一下《Transimpedance Considerations for High-Speed Amplifiers》,噪聲增益曲線中反饋電阻R_f和反饋電容Cf形成的極點頻率除以諧振頻率fo等于Q,那么根據Q和f_o就可以求出Cf,而當Q=0.707時,fo=f-3dB:
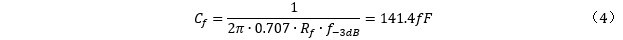
TI有一個Excel計算工具,可以幫助您完成設計,見《What you need to know about transimpedance amplifiers – part 2》
5. Decompensated amplifier在TIA電路中的應用
Decompensated amplifier是一種通過犧牲穩定性來提高性能的,單位增益下不穩定的運放。 與單位增益穩定運放相比,去補償的放大器在使用更少的電流的同時,可以獲得更高的增益帶寬乘積,更低的噪聲,更高的壓擺率。

對于如圖1 理想的跨阻放大器電路而言,只有反饋電阻的存在,這種情況下,噪聲增益為1,那么對于decompensated amplifier而言,因為單位增益不穩定的原因,去補償放大器是不適合這種情況的。
但是,對于實際的跨阻放大器電路而言,由于Cs和Cf的存在,將Noise Gain 將會穩定在(1+Cs/Cf),這樣
1)確保了decompensated amplifier能夠工作在穩定的狀態。
2)因為decompensated amplifier的開環增益曲線相比單位增益放大器的開環增益曲線,向上和向右拓展,因此避免了使用單位增益放大器的Loop Gain 以-40dB/dec速度下降的可能,同時提高了該放大電路的閉環帶寬。
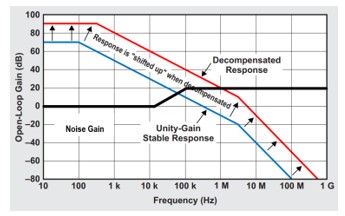
圖 14 Decompensated amplifier與單位增益放大器開環增益的區別
所以Decompensated amplifier是天然適合跨阻放大電路的應用。
審核編輯:郭婷
-
電容
+關注
關注
100文章
6259瀏覽量
154433 -
放大電路
+關注
關注
105文章
1815瀏覽量
108174 -
adc
+關注
關注
99文章
6716瀏覽量
549454
發布評論請先 登錄
跨阻結構的優點是怎么的來的?
一些TINA-TI的技巧和竅門
TINA-TI還可以做哪些事
如何使用TINA-TI仿真可能包含非TI器件的電路?
TINA-TI電路設計及仿真軟件入門教程說明





















評論