1 數的表示與布爾代數

1.1 數的編碼與二進制表示

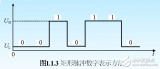
編碼是各種集合的元素映射到字符串的過程 。數字電路中的數字表示就是一串用已約定好的表示的 0 和 1 的組合。二進制的優點：

運算簡單 ——算術運算加法和乘法僅各有3條規則不易出錯 ；邏輯運算可與“真”“假” 對應

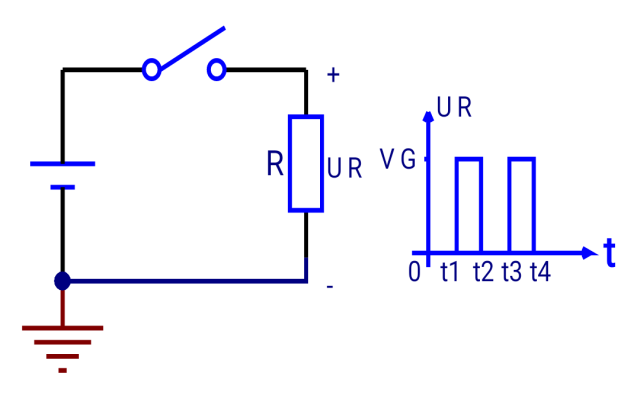
存儲簡單 ——高低電壓表示兩種狀態；有更大的噪聲容限

1.1.1 常見的編碼

二元編碼 ——條形碼

BCD碼 ——會計系統長數字串計算

格雷碼 ——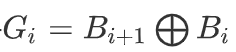，其中B為二進制編碼首位補一個0。九連環341種狀態。2G一改零不改，G2奇變偶不變

1.2 二進制補碼表示

1.2.1 補碼分類

有符號數 ——開頭位0正1負

1補碼 ——負數對應的二進制正數 N 按位取反，2n-1-N。0有兩種表示，-(2n-1-1)~2n-1-1

2補碼 ——按位取反再+1，2n-N。0有唯一表示便于減法轉加法，-2n-1~2n-1-1

1.2.2 溢出判斷

對數字最高有效位進位和符號位進位做異或，為1則溢出；或滿足其一即可判別：

符號異常 ——兩個加數符號位相同但是與結果符號位不同

進位異常 ——內部進位（結果的符號位）≠外部進位（結果擴展位）

1.3 邏輯與布爾代數

1.3.1 基本定理

交換，結合，分配，互補，01，重疊，對合

對偶 ——與或互換，01 互換，布爾變量不變

多數 ——(X+Y)(Y+Z)(X’+Z)=(X+Y)(X’+Z) ， XY+YZ+X’Z=XY+X’Z 可用于消除競爭冒險

1.3.2 德摩根定理

與或互換，01 互換，布爾變量求反得到 反函數 （注意到和對偶只相差是否變量求反）

一般來說，將布爾函數表示成與非門，可以用最小的代價實際映射到電路

1.4 布爾函數表示

程序表達、二分決策圖、真值表、卡諾圖、邏輯電路

1.4.1 兩級邏輯

最小項或=互補序號的最大項與

1.4.2 布爾代數化簡

代數化簡 ——并項、吸收、消去、配項（冗余定理）

卡諾圖化簡 ——能夠蘊含一個函數的與項是 蘊含項 ；不存在蘊含項 I≠P，使得 P => I => F，則稱 P 為 本原蘊含項 ；某個元素僅由一個本原蘊含項覆蓋，則該蘊含項為本質本原蘊含項

QM化簡 ——搜索本原蘊含項，尋找最小覆蓋

在邏輯表達式中，如果能夠將信號合并使得輸入端出現 盡可能少的信號種類 ，那么就有可能減少整個門電路的MOS管個數

2 組合電路與邏輯綜合

在實際電路中，想要實現與/或門，一般都采用 NAND/NOR + 非門的形式。組合邏輯是當前的輸入變量取值決定當前的輸出的 無記憶元件 ，且輸出是輸入邏輯變量的函數。

CMOS ——高密度、低功耗，系統成本低，適用于主流數字系統

BJT ——超高速、超低噪聲，適用于高速應用例如一些模擬和射頻電路

2.1 組合邏輯分解

多級邏輯的基本表示方法是 復合函數 。一方面類似因式分解將函數計算進行分解化簡；另一方面可以共享中間層次的計算。

2.2 組合邏輯中的競爭與冒險

毛刺 ——出現在組合邏輯電路輸出端的多余脈沖，本應保持不變的輸出值出現了瞬時變化。輸出的毛刺是單端輸入取值變化的結果

冒險 ——有可能產生毛刺的電路存在冒險，冒險是一個電路的固有特征，存在冒險的電路可能產生毛刺，也可能不產生毛刺

靜態冒險 ——一個本應保持不變的輸出經歷瞬時轉換

• 靜態1冒險：取值為1的輸出瞬時經歷0狀態
• 靜態0冒險：取值為0的輸出瞬時經歷1狀態

動態冒險 ——本應單次跳變的輸出信號發生不止一次的跳變

• 多級電路存在多條路徑，且這些路徑的延時是不對稱的
• 一個無靜態冒險的多級網絡仍可能存在動態冒險

2.2.1 組合邏輯靜態冒險消除

增加冗余 ——如果輸入初始值和輸入最終值能被同一個本原蘊含項覆蓋，則不會出現毛刺（靜態1冒險）。

采樣脈沖 ——采樣脈沖在D穩定期間進行采樣

2.3 評價邏輯電路的主要指標因素

2.3.1 穩態因素

邏輯電平 ——邏輯0和1對應的電壓范圍越寬，抗干擾的能力越強，對電子元器件參數精度的要求及電源電壓范圍的穩定度的要求越高

噪聲容限 ——輸出電壓與輸入電壓之間的電壓差稱為噪聲容限

扇出系數 ——最壞負載情況下一個邏輯門能驅動的輸入端數目。TTL電路的扇出系數一般小于10，MOS電路的扇出系數不受負載影響，但是隨著扇出的增大，負載電容增大，導致工作速度大幅下降

2.3.2 動態因素

轉換時間 ——邏輯門的輸出從一個狀態變化到另一個狀態所用的時間

延時 ——從邏輯門的輸入發生變化到相應的輸出發生變化所用的時間，會導致冒險的存在

功耗 ——分為動態功耗（CMOS由開關電流和短路電流引起）和靜態功耗

• 開關電流是不斷對負載電容充放電所產生的
• 短路電流是輸入存在有限轉換時間引起PMOS/NMOS同時導通形成的

低功耗技術 ——降低電路的功耗以延長壽命，應該降低電路的電壓和頻率，導致工作速度下降 ，因而追求低功耗延時積

2.4 常用的邏輯功能的實現與優化

2.4.1 傳輸門

使能控制信號EN為低電平時，TG截止，F為 高阻態 ——相當于懸空，如果用萬用表測可能是高電平也可能是低電平

總線應用 ——各門的控制端EN輪流單獨為高電平

2.4.2 編碼器/譯碼器

編碼器 ——按照輸入是否有優先級分為普通編碼器（單1）和優先編碼器（多1）

譯碼器 ——每個輸出對應一個最小項

2.4.3 多路選擇器

對應通過地址查表的過程。2n個數據輸入, n個選擇輸入，1個數據輸出

n變量邏輯函數 ——函數輸入變量加到地址端，數據輸入端賦值

m(>n)變量邏輯函數 ——函數的m-1個輸入變量加到地址端，數據輸入端以第m個輸入變量的邏輯關系賦值

• m=n+1時，不需要任何附加的邏輯門

2.4.4 加法器

半加器不考慮進位；全加器考慮進位，輸和Si和進位Ci+1

串行加法器 ——電路簡單、速度慢

并行加法器 ——電路復雜、速度快

組內并行、組間串行進位加法器 ——層次化設計，解決扇出增大導致的加法器延時

3 時序邏輯與FSM

3.1 基本概念

過程在數學上可以表示為時間的函數。過程需要用不同的狀態表示，這些狀態需要用記憶元件來控制和預測

3.1.1 過程離散化與時鐘

過程離散化 ——即時間離散化、狀態數字化。將過程離散化是為了充分利用數字信號處理的快捷和高效

時鐘 ——分布于包含記憶元件的電路中的一個周期信號，用來同步控制所有時序單元。保證所有元件都在同一時刻改變狀態的是 同步電路 ，沒有時鐘或不使用同一個時鐘信號的是異步電路

擺率 ——在單位時間里電壓升高/下降的幅度，影響上升和下降沿時間

時鐘信號產生 ——利用電路中的延時，采用反相器或者環形振蕩器

3.1.2 時鐘域與同步處理

時鐘域 ——所有同步于同一個時鐘信號的信號集合。同一個時鐘域中的信號只能由同一個時鐘的時鐘沿來觸發，時隙內所有的信號不會發生變化

跨時鐘域 ——在兩個不同的時鐘域之間傳遞數據，二者時鐘頻率不一樣，或者頻率相同但存在相位差，來自一個時鐘域的信號被另一個時鐘域認為是異步的輸入信號

同步處理 ——當數據與采樣時鐘異步時，或跨時鐘域時，就需要對信號事件順序的決定和處理。

3.1.3 狀態

狀態 ——系統的基本數學特征

時序邏輯需要將輸入信號的歷史信息存儲下來。而狀態變量的取值就是用來記錄電路過去的信息，從而說明電路將來的行為

3.1.4 有限狀態機

狀態機 ——離散數學模型，給定一個輸入集合，根據對輸入的接收次序來決定一個輸出集合

有限狀態機 ——輸入集合和輸出集合都是有限的，且狀態數目是有限的。有限狀態集合S，有限輸入符號集合I，有限輸出符號集合O，初始狀態s0，狀態轉移規則f ，輸出規則h

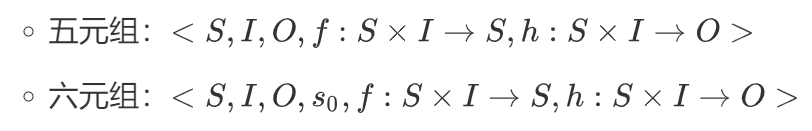** Mealy機** ——輸出依賴于當前的網絡狀態和當前的輸入

Moore機 ——輸出只依賴于電路當前的狀態，和當前輸入無關

狀態轉換表 ——有限狀態機的描述方法：輸入、現態、次態、輸出

3.2 鎖存器

鎖存器 ——在任意時刻都連續監測其輸入，并改變其輸出狀態，與有無時鐘信號無關。鎖存就是將信號暫存以維持某種電平狀態，在計算機或數字系統的輸入緩沖電路中廣泛使用。這樣可防止輸入信號的各個位到達時間不一致造成競爭與險象

可以有時鐘信號作為控制端，在有效期間時刻檢測輸入取值，具有透明性

3.2.1 SR 鎖存器、D 鎖存器

SR鎖存器 ——

門控SR鎖存器 ——C=1時S置位R復位，C=0時狀態不變

時序電路的競爭 ——最終電路產生的狀態與時間相關，且不能事先預測，通過約束輸入取值來避免競爭條件的出現

門控D鎖存器 ——C=1時隨D變化，C=0時狀態不變

3.2.2 鎖存器的時間參數

最小脈寬 ——為了得到希望的輸出結果，輸入信號有效的最短時間

延時 ——輸入信號發生變化，導致輸出信號發生相應變化的時間

建立時間 ——鎖存操作開始之前，輸入信號應保持不變的最短時間

保持時間 ——鎖存操作之后，輸入信號還應保持不變的最短時間

3.2.3 亞穩態

亞穩態 ——不確定狀態。若信號不滿足建立時間與保持時間約束，在時鐘的上升沿采樣的信號正在發生變化，則輸出可能為1或0

產生原因 ——不同時鐘域的存在，時鐘偏差的普遍存在

解決方法 ——同步器設計，異步FIFO，被采樣信號滿足建立時間與保持時間約束

3.3 基本時序邏輯單元——觸發器

觸發器 ——僅在時鐘信號有效時采樣輸入，并改變其輸出狀態

3.3.1 主從SR觸發器

主從觸發器 ——脈寬觸發的觸發器，可避免鎖存器的透明性。在控制信號發生改變時，觸發器狀態發生相應的變化。具有一個主觸發器和一個從觸發器

主從SR觸發器 ——高電平主觸發器置位復位，下降沿從觸發器獲得主觸發器之前的狀態

3.3.2 邊沿D觸發器

邊沿觸發器 ——利用時鐘的上升沿或者下降沿進行觸發，改變輸出。只要在觸發沿處，輸入的取值在建立時間和保持時間內固定不變，在觸發器的固有延時之后立即發生相應的變化

邊沿D觸發器 ——高電平主觸發器置位復位，下降沿從觸發器獲得主觸發器之前的狀態

3.3.3 JK觸發器與T觸發器

JK觸發器 ——相比SR觸發器，JK=1時狀態反向

T觸發器 ——0不變1反向

3.3.4 觸發器的時間參數

建立時間 ——觸發器時鐘沿到來之前輸入信號應保持不變的最短時間

保持時間 ——觸發器時鐘沿到來之后輸入信號還應保持的最短時間

輸出響應時間 ——從開始采樣到輸出信號的延時

3.4 同步時序電路分析和設計方法

避免反饋振蕩 ——插入時鐘控制的觸發器

3.4.1 同步時序電路的分析方法

1. 寫出各觸發器的激勵方程（ 驅動方程 ）
2. 把得到的驅動方程代入到觸發器的特性方程，得到次態方程
3. 按照電路圖得到輸出方程
4. 根據次態方程和輸出方程得到狀態表
5. 得到時序電路的狀態圖
6. 畫出時序圖
7. 確定電路行為

3.4.2 Moore機和Mealy機輸出時序對比

理論分析時僅在時鐘觸發沿時刻考慮外部輸入對時序電路的影響，而米利型電路的輸出與外部輸入時時刻刻都相連

Moore輸出 ——狀態數更多，與時鐘同步

Mealy輸出 ——狀態數更少，與時鐘異步，輸入變化則立即變化。可通過觸發器消除時序關聯

3.4.3 同步時序電路的設計方法

等價狀態對 ——當且僅當它們輸出相同、次態等價

狀態不等價 ——至少有一種輸入序列會使得它們作為起始狀態時產生不同的輸出序列

1. 確定輸入輸出并抽象出有限狀態機，得到狀態表或狀態圖
2. 狀態化簡 ——行匹配技術（合并具有相同次態和輸出的行）、蘊含表技術（輸出不同x，次態輸出都相同√，其他待定）
3. 狀態分配
   • 順序編碼（二進制/格雷）
   • 隨機編碼、緊湊型編碼、單點編碼、面向輸出的編碼
   • 啟發式方法（最少位變化：基于次態和輸入/輸出的準則[*]）
4. 確定激勵方程和輸出方程
5. 畫出兩級或者多級邏輯電路圖

[*]基于次態和輸入/輸出的準則

Rule I ——具有相同次態的狀態應該具有相鄰的狀態編碼

Rule II ——同一狀態的次態應該具有相鄰的狀態編碼

Rule III ——具有相同輸出的狀態應具有相鄰的狀態編碼

3.4.4 典型的時序邏輯電路——寄存器

（存儲）寄存器 ——數字系統的存儲元件，由n個觸發器構成

移位寄存器 ——數字系統中既能寄存二進制信息又能移位的邏輯元件，分為左移寄存器、右移寄存器、雙向移位寄存器。也可按照并/串行輸入輸出分類

串行輸入 ——簡單，存儲時間長（n周期）

并行輸入 ——多路選擇實現移位/加載模式，單周期全加載

串行輸出 ——僅最后一個存儲單元值可見，減少輸出端數目

并行輸出 ——所有觸發器儲值可見

3.4.5 典型的時序邏輯電路——計數器

計數器 ——記錄輸入脈沖的個數，其最大值稱作 模 ，用于定時、分頻、產生節拍脈沖及數字運算等等。可以分為加法、減法、可逆計數器；特殊進制計數器；利用移位寄存器構成的計數器

自啟動 ——非正常工作狀態能經過若干次狀態轉換進入正常工作狀態

1. 增加組合電路
2. 利用觸發器預置位和復位端重新加載觸發器狀態使回到正常序列或起始狀態

環形計數器 —— 循環的移位寄存器 。將移位寄存器的串行輸出接回串行輸入。電路簡單，浪費狀態

扭環形計數器 ——將移位寄存器的串行輸出反接回串行輸入。加倍模值，提高狀態利用率。

異步計數器 ——低位計數器的反向輸出是高位計數器的時鐘信號，低位都為1時高位才翻轉，最低位每次翻轉

同步計數器 ——組合邏輯實現翻轉規則：與門輸入數目增加或延時增加