導讀：本篇博文我是想盡可能囊括足夠多的DOA估計方法。DOA算法其理論的理解和公式的推導需要較強的數學功底以及信號處理相關知識的積累，博主本人是轉專業來的，是該方向的后聞道者，且入行沒多久，相關的理論知識積累少也不扎實，涉及到的公式非必要我會盡量少放。本篇博文不會討論這些DOA估計算法的具體原理/公式推導(相關的資料在網上有很多)，而是側重于試圖搭建一個常見的適用于(或可能適用于)車載毫米波雷達的DOA估計方法的框架。

車載毫米波雷達DOA估計方法概述

目標角度估計，特別是角度分辨率的提高是雷達探測需要解決的核心問題，傳統的車載毫米波雷達其實對角分辨率的要求并不高，幾度甚至十幾度的角分辨率是很多商用角雷達與前向雷達的測角指標，且這些雷達并不具備俯仰向測角能力。但是隨著輔助駕駛乃至無人駕駛對傳感器的要求越來越高，二維測角能力以及更高的角分辨率(甚至低于1°)成為了車載毫米波雷達的標配。比如近幾年發展起來并開始逐步商用的4D毫米波雷達。

使用FFT與DBF做DOA估計是最簡單且運算復雜度最低的方法，但是這兩方法并不能實現超分辨，其角分辨率受限于陣列的孔徑，比如對于均勻排布的陣列，角分辨率有公式：

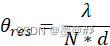
式中，N為陣元個數，d為均勻陣的相鄰陣元間距，該式得到的是雷達法向的角度分辨率。從上式可以看出，如果要提高角分辨率那只能通過增加天線數量來增加陣列孔徑，但是天線數量和孔徑不能不受限地增加，否則包括硬件成本、數據量、尺寸等都沒法滿足實用要求。

于是催生了所謂的壓縮感知：期望使用較少數量的陣元通過稀疏布陣的方法以達到較高的測角分辨率，關于壓縮感知，又有多種針對稀疏陣列的測角方法:

1、還是直接對稀疏陣元使用DBF測角，此時相較于均勻陣列，必然有很多空缺的陣元，這些空缺的陣元會導致很多很高的旁瓣出現，如下圖所示：

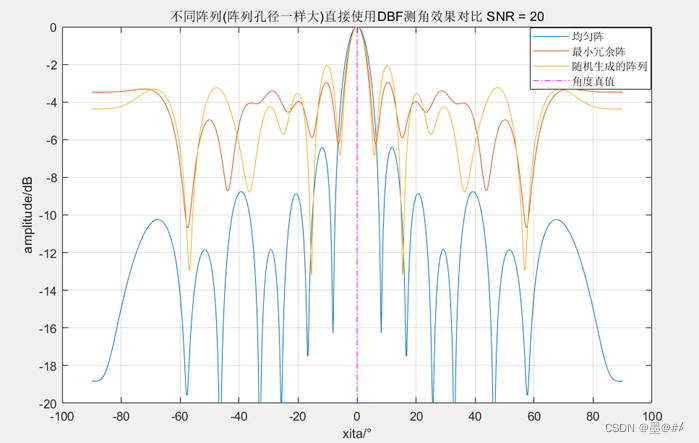
同陣列孔徑下，均勻陣與稀疏陣的陣列方向圖對比

仿真中，均勻陣的大小為[013],最小冗余陣對應[0 1 2 6 10 13]，生成的隨機陣列為[0 1 2 5 11 13]，從圖中可以看到，當陣列中有空缺的陣元時，直接使用DBF或許也能看到目標的位置，但是旁瓣極高。當目標不止一個或者SNR值很低，此時稀疏度較高的陣列直接使用DBF測角是不適用的，如下所示：

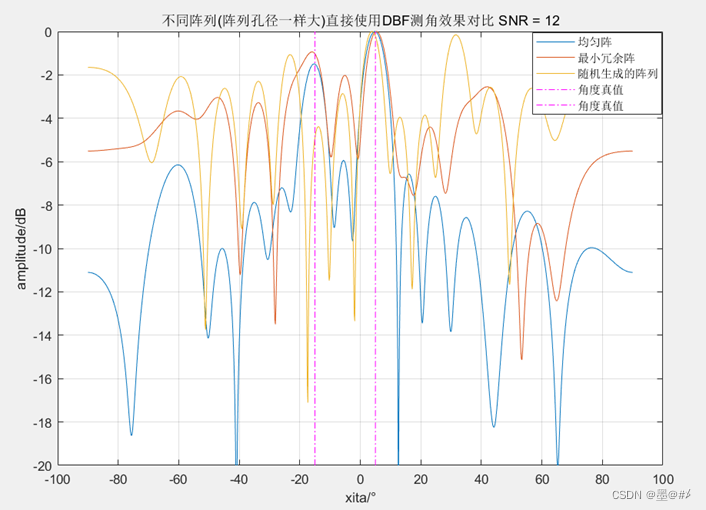
從圖中可以看到，只有均勻陣的還能準確地分辨出兩個目標。

2、陣元補全：將空缺的陣元位置的信息通過一些方法(在后文做介紹)進行補全，隨后再使用DBF等方法基于補全后(等效為均勻陣了)的陣列信息做角度估計。這種方法可以達到近似均勻陣的效果，但是運算量會上來，且補全算法的可實用性可能對依賴于特殊的陣列。

3、基于凸優化或者貪婪近似方法做超分辨的角度估計，比如正交匹配追蹤算法OMP以及迭代自適應算法IAA等，這兩種方法允許陣元不全（自然它們也可以用于均勻陣！），且其相較于其它超分辨算法，它們不需要多快拍數據、也不需要提前知道信號源的個數，但是計算量大。

除此之外，則是一些超分辨算法了，常見(但是不常用于車載毫米波雷達)的包括：最大似然估計(DML，DML作為一種需要多快拍也需要提前知道信源個數的超分辨率測角算法很意外地在實際產品中被廣泛使用，特別是基于加特蘭的芯片開發的雷達產品，加特蘭在其芯片中將該算法硬化了)、Capon、MUSIC、ESPRIT等超分辨測角算法，但是這些超分辨算法其測角結果的準確性大多依賴于多快拍的回波數據以及信號的高SNR。

如前所述，現階段對車載毫米波雷達的要求已經不限于一維測角了，當需要做二維的角度估計時，就又產生了諸多的2D-DOA估計方法，2D-DOA估計最簡單是對面陣做2D-FFT或2D-DBF，隨后在得到的矩陣中找極大值，并根據該極大值所在的索引值得到目標的二維角度。在該方法的基礎上，一種容易想到的改進方法是：首先對測角面陣只做水平向或豎直向的FFT或DBF，隨后找到其極值點，并得到水平向或豎直向的角度值，再對這些極值點所在的另一維度做FFT或DBF,得到豎直向的角度以完成2D-DOA估計，基于面陣直接進行二維壓縮的方法不需要進行角度匹配，算法簡單，但是對陣元數的要求高。另外的一些方法則是分別在水平和豎直向做獨立的角度估計，再基于一些匹配方法做目標水平和豎直向的角度匹配以完成目標的2D-DOA估計，這類方法并不需要是面陣，減少了天線數量但是算法復雜度上升。我會在后文中簡單介紹兩種匹配方法。

總結來說，后文將涉及：FFT、DBF、IAA、OMP、DML、Capon、MUSIC、ESPRIT等測角算法、稀疏陣列補全方法、目標2D-DOA估計方法，并簡要討論超分辨算法在車載毫米波雷達中實用的可行性。在此重申，相關的內容比較少涉及具體的公式推導(但是我會盡可能多地提供相關的測角效果對比，相關的仿真代碼等閱讀量到一定程度后再公開)，內容會隨著積累不定期豐富。

補充說明：

前文提及到了4D毫米波雷達，4D毫米波雷達性能評價的最核心指標便是角度分辨率，這里對現階段商用4D毫米波雷達的幾種實現路線做一個簡單介紹，現階段商用4D毫米波雷達產品主流的實現方式主要有4種：

1、級聯的方案：通過多芯片級聯來增加通道數，主流的Tier1比如大陸、博世、安波福，以及華為的4D毫米波雷達都是用的多芯片級聯方案。

2、“單芯片”方案：這種方案的出發點和級聯方案是一樣的，只不過是做出了更厲害的芯片，在單顆芯片上便實現傳統芯片多芯片級聯才能達到的通道數，比如Arbe的48T48R產品僅僅使用了2顆發射芯片和4顆接收芯片，且其數據處理部分也有專用芯片。

3、軟件手段：對實際通道數的要求低，只需要很少量的通道數，該技術路線通過算法和軟件的方法構建虛擬通道使分辨率成量級地提高。比如傲酷。

4、超材料方案：MetaWave的超材料成像雷達，大概是基于材料的特殊特性，通過波束掃描(相控陣)來實現極高的角分辨率。

幾種常見的DOA估計方法及其對比總結

陣列的DOA估計需要明白的一點是：測角算法應該是需要與具體的陣列相結合的。合格的毫米波雷達產品應該是合適的陣列設計再加上對應的合適的信號處理(測角)算法。

2.1 FFT與DBF

這兩是最簡單的測角算法，且效果幾乎一致。最早的基于陣列的DOA算法便是常規波束形成算法（CBF或DBF），DBF本質是構造視場范圍內的各個角度的導向矢量，并用這些導向矢量分別去和陣列的回波信號相乘以得到各個角度下的能量值，我們通過尋找其中的極大值(目標所處方向的回波與導向矢量相干疊加，這些方向的能量會得到增強，而噪聲是非相干的，能量得到增強的方向，對應極大值的位置，也即信號的方向)來得到實際回波的方向而達到測角的目的。與時域相比，測角是以空域各陣元接收的數據替代傳統時域處理中的時域數據，所以與時域的傅里葉限制一樣(FFT后的頻率分辨率取決于采樣時間: df = 1/T)，將這種方法擴展至空域后，陣列的角分辨率同樣受到空域傅里葉限(此時是陣列的孔徑：θres=λ/(N*d)的限制。如果要提高測角分辨率就只能通過增加孔徑來實現。以下給出不同陣列孔徑下的DBF與FFT的測角效果：

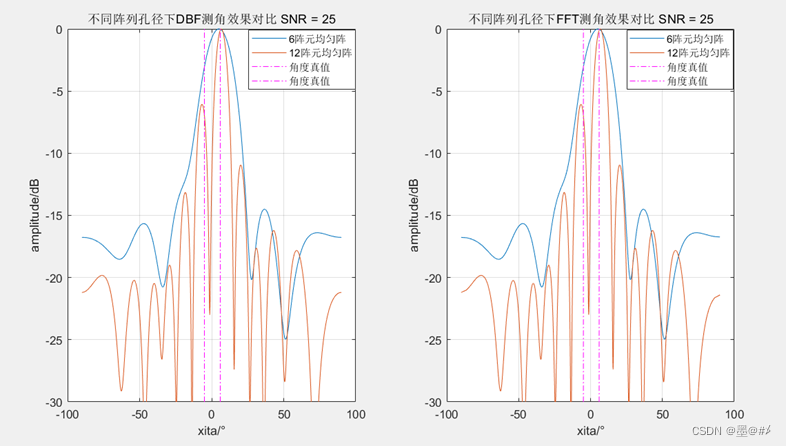
不同陣列孔徑下的測角效果對比

FFT與DBF的測角效果一致。為方便比較，后續各種測角算法下的測角效果都會將之與DBF下的測角效果做對比。

2.2 Capon(或稱MVDR，最小方差無畸變算法)

波束形成的算法有很多(可以參考之前提到的書：《陣列信號處理及MATLAB實現》，Capon是其中較為經典的一種，除此之外還有比如：MMSE、MSNR等)，前述DBF嚴格來說應該稱為CBF（常規波束形成），是最簡單的一種波束形成算法，這么多波束形成算法其主要區別在于前面提及的導向矢量(或權矢量)的不同，比如前述CBF的導向矢量為：

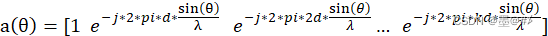
式中，d為陣列陣元之間的間距，k為陣元個數，θ在測角范圍內變化，我們用上述向量去和回波信號相乘，得到不同角度下的能量結果。而對于Capon算法，其權矢量變成了：

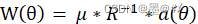
式中，a(θ)同前式，R為信號的協方差矩陣，θ在測角范圍內變化，μ為常數，對應特定方向下經過該Capon算法后的能量值，結合約束條件：

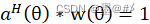
可以得到不同角度下的能量值的估計式為：

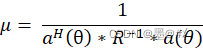
在該式的指導下，我們求解并得到不同角度下的能量值，找到極大值點的位置即可得到目標的角度。注意到信號協方差矩陣R的準確估計依賴于多快拍的回波數據以及高的SNR，所以該算法需要多快拍數據做支撐。不同快拍數下的效果對比如下：

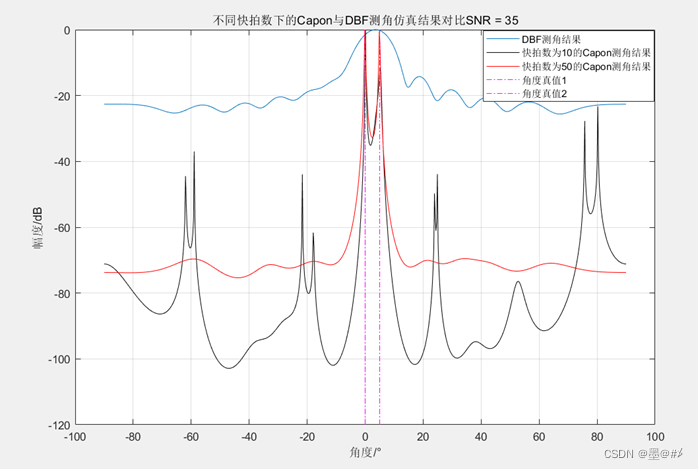
12陣元均勻陣下的Capon與DBF仿真結果對比

目標處在0°和5°，可以看到DBF下無法做到超分辨，但是Capon算法下看到了兩個明顯的峰，做到了超分辨測角(該算法可以做到多少倍的超分辨主要與SNR有關)，仿真結果中還給出了不同快拍數下的Capon算法對比，可以看到多快拍數下的測角結果明顯優于低快拍數(這是一個比較定性的說法，至于在特定的SNR下多少快拍數可以滿足測角要求，不在本博文的討論范圍之內)。

2.3 MUSIC & ESPRIT

這兩都是基于協方差矩陣的特征分解類DOA估計算法，都是非常優良且經典的超分辨DOA估計方法。MUSIC相對容易理解一點，利用的是噪聲特征向量與信號向量的正交關系，ESPRIT是基于信號子空間的旋轉不變性？具體的原理我理解一二但是很難簡單說清楚，讀者可以參考前面提到的書本。

這兩種方法相較于前面的Capon算法除需要較多的快拍數和高的SNR以得到精確的協方差矩陣估計外，還需要知道信源個數，這是限制其應用于車載毫米波雷達的另一個重要原因。【不過對于非4D雷達，我們在做角度測量時可以限制其一個距離和速度門下只有一兩個目標？后文將提及的DML算法也需要知道信源個數，限定信源個數是加特蘭芯片中應用DML算法的一個基本前提。】具體到這兩種超分辨算法，MUSIC對信源個數的要求似乎不那么嚴格一些，比如實際目標有3個，使用MUSIC算法是給定目標個數大于等于3時，其測角的波峰結果仍會是3個，而如果給定目標個數小于實際目標個數，則測角的波峰結果會等于給定的目標個數。而ESPRIT的輸出結果等于給定的目標個數，不管實際的目標個數是多少。

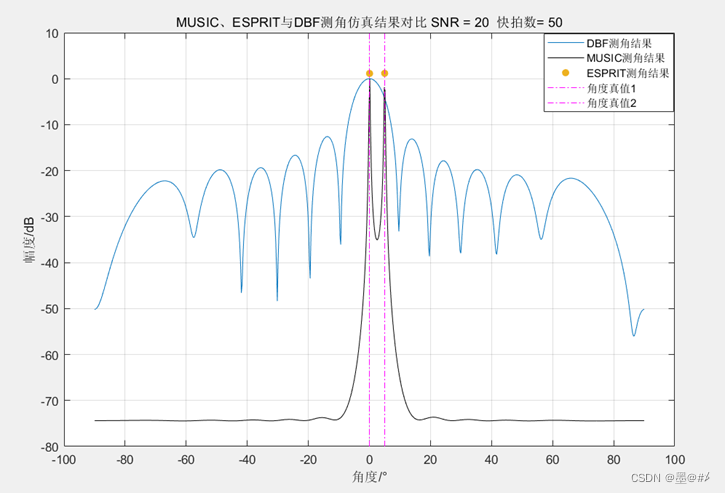
12陣元均勻陣下MUSIC、ESPRIT與DBF測角結果對比

目標在0°和5°位置，MUSIC和ESPRIT都準確地估計到了目標，具備超分辨能力，但是DBF下兩目標隱藏在了一個波峰里面。同Capon中的說明，SNR越高和快拍數越多，其超分辨的能力越高，不過固定的快拍數下，這兩算法對SNR的要求相比Capon似乎要低一些，此外其實這兩算法對快拍數的要求也不是太高(但是單快拍是不行的)，幾個快拍加上比較好的SNR超分辨的效果就很好了。

2.4 DML(最大似然法)

在《陣列信號處理及Matlab實現》這本書中，對DML的介紹是：在信號處理中，最著名和最常用的建模方法是最大似然法。基于最大似然的波達方向估計方法分確定性最大似然法(Deterministic ML，DML)和隨機性最大似然法(Stochastic ML，SML)兩大類型，我們這里討論和使用DML。

具體的原理可以參考書本，我后面所做仿真是基于加特蘭baseband中對其DML算法的介紹而寫的代碼，原理比較簡單，我直接貼那段話的圖吧：

加特蘭Baseband使用手冊中對DML算法的介紹

其中A(θ)為導向矢量矩陣，X為接收信號，R為信號的協方差矩陣，本算法是要求出使得P*R這個矩陣的跡最大時對應的角度(或如果有多個目標的話，則是角度集合)，算法是要做遍歷的，且在特定的角度掃描個數(比如從-75°到75°設定角度掃描個數為N)下其算法復雜度和信源個數D的關系為：Ο(ND)。DML算法也是需要多快拍的數據以及知道信源個數的，上面提到過加特蘭在其芯片中應用該算法的一個基本前提是對一個距離和速度門下的目標個數做了限定(不超過兩個)，而且信源個數一多計算時間也會增加，而車載雷達對更新率是有要求的，此外，加特蘭在其baseband中說According to the result of simulation, DML performs well in some respects. It can separate incoming signals with small angle differences even in single snapshot case, so in our DML engine, we use only one snapshot to do the angle estimation，用單快拍的數據來獲得協方差矩陣在DML中似乎也可以接受。以下為DML和DBF的仿真結果對比：

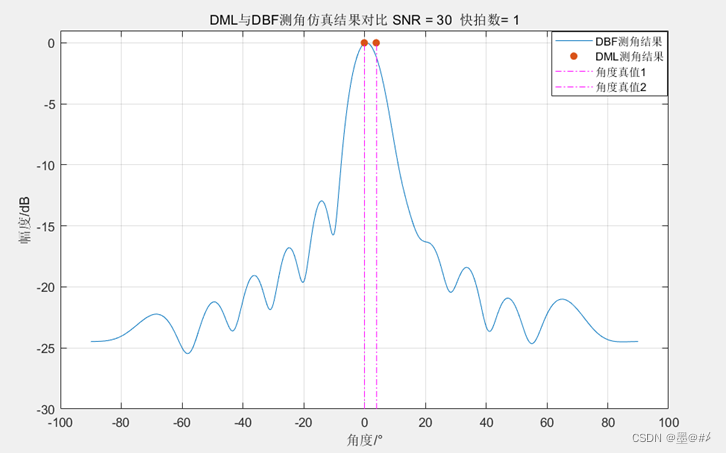
12陣元均勻陣下MUSIC、ESPRIT與DBF測角結果對比

目標在0°和4°的位置，DML算法準確地測量到了目標，且做到了超分辨。DBF下兩目標隱藏在了一個波峰里面。此外，仿真結果顯示，DML算法對SNR的要求較高。

2.5 OMP(Orthogonal Matching Pursuit 正交匹配追蹤算法)

OMP是一種信號重構算法，將該算法用于角度估計的基本原理是：假設有K個目標，入射到M個天線構成的均勻線陣上，設第K個信號的入射角度為θk,則陣列t時刻接收到的信號為：

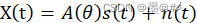
式中，A為信號的方向矢量矩陣，s為信源矢量，n為噪聲。(這個公式比較簡單，容易理解，就略過了)，我們將A進行拓展，A之前的大小是K*M，K表示K個目標方向，將之擴展到包含雷達視場范圍內的所有可能的方位角(比如[-7575])，此時假設其大小變成了N*M，我們用G表示，此時上式變成：x = G*γ+n，γ為N維的系數向量，且由稀疏理論可知，γ中非零元素個數應該為K(目標個數)，γ中非零元素的位置對應向量的對應角就代表了入射角θ的值，我們可以用OMP算法求解該問題（等價于求解擴展后的方向矢量矩陣中各個角度的貢獻值：知道了G和x來求γ，就是上面博客中的問題）。

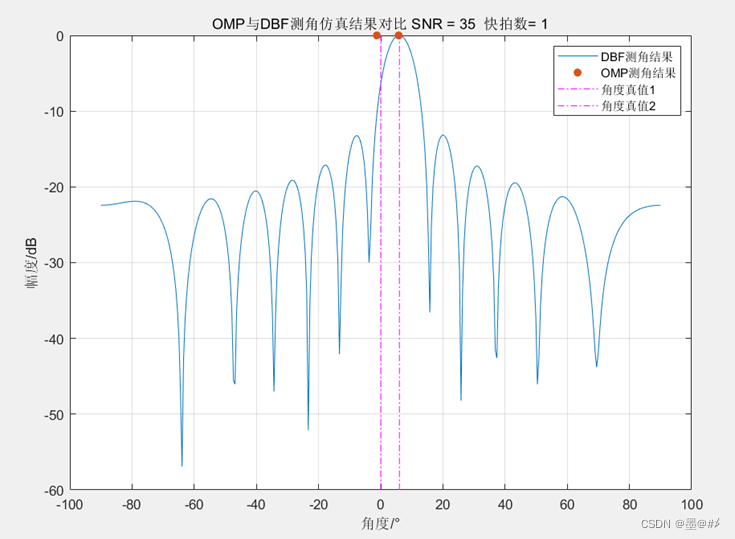
12陣元均勻陣下OMP與DBF測角結果對比

目標在0°和5°的位置，OMP算法差不多準確估計到了目標位置(精度有些問題，大概是寫的OMP算法有點不對..), DBF下兩目標隱藏在了一個波峰里面。OMP算法只要求單快拍的數據，但是需要知道信號源的個數。

2.6 IAA(Iterative Adaptive Approach,迭代自適應法)

網上對IAA算法的介紹好像很少，IAA是一種基于加權最小二乘法的非參數方法，具體的理論我也講不清楚，后面找到比較好的介紹資料我再貼出來，這里直接給出仿真結果：

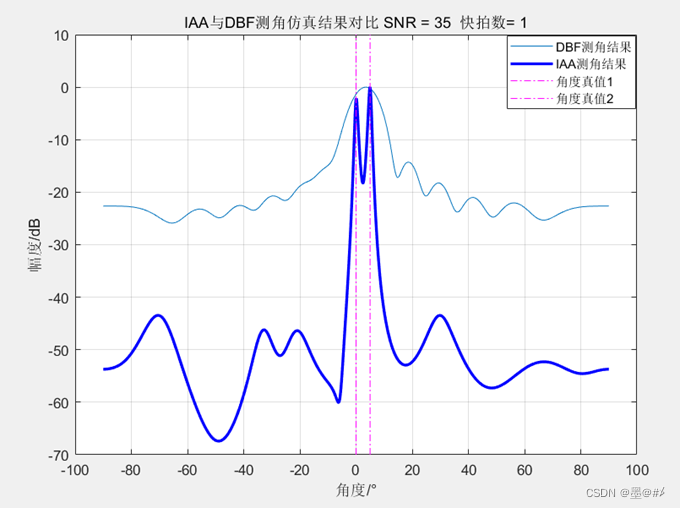
12陣元均勻陣下IAA與DBF測角結果對比

目標在0°和5°的位置，IAA算法準確地測量到了目標，且做到了超分辨。DBF下兩目標隱藏在了一個波峰里面。此外，仿真結果顯示，IAA算法雖然可以在單快拍下測角，但是如果SNR也很低那么超分辨的效果將很差(超過角度分辨率一點點可能就分辨不出來了)。該方法需要知道信源個數。

2.7陣元補全

本小節的內容討論稀疏陣下的空缺陣元補全的方法，所謂的陣元補全就是基于實際的稀疏陣列排布和實際存在的陣元所接收到的信號，采用一定的方法將相較于均勻陣列空缺的位置的回波信息恢復出來(在此過程中也可能會改變原有陣元位置處的原始接收信息)。之后基于恢復后的(不那么稀疏的)陣列進行測角等處理。

這里給出兩種方法，并給出陣元補全前后以及同等孔徑均勻陣下的DBF測角結果對比。

A、基于協方差矩陣向量化與差分集合

有一篇碩士畢業論文比較清楚地講解了該方法的原理，但是找不到了(后面如果找到我再貼上來)。該方法首先求解稀疏陣列所接收回波數據的協方差矩陣，隨后將該矩陣向量化，按照原稀疏陣列對應的差分集合中元素的順序和值，選取對應的協方差矩陣向量化后的元素來構造等效的（更均勻）的接收陣列回波數據。該方法需要多快拍的數據，且差分集合中的值重復得越少對應恢復的效果越好，最小冗余陣列其差分集合中的值都是唯一的，所以用該方法恢復最小冗余陣列性價比最高。

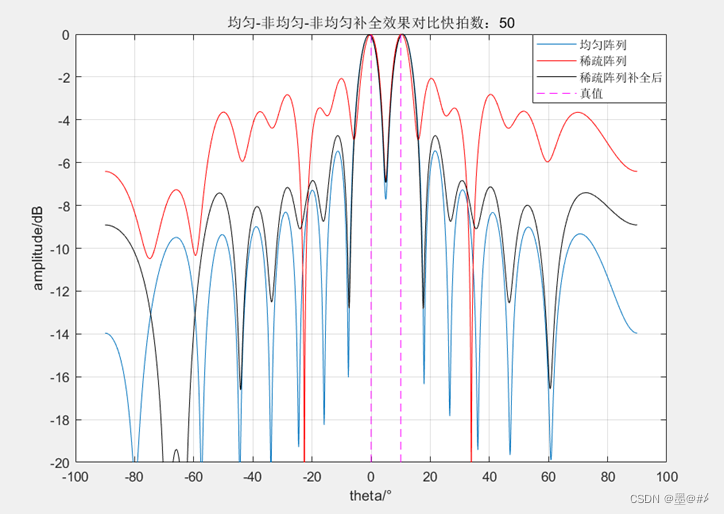
6陣元最小冗余陣[0 1 2 6 10 13]的補全前后仿真效果對比

目標在0°和10°的位置，可以看到，使用該方法進行陣列補全恢復后的測角效果與均勻陣下的測角效果幾乎一致，而恢復前因為有大量空缺的元素存在，導致旁瓣拉高(我在前述第一章中有說明)，這也是陣列補全的意義所在。此外從仿真的結果來看，使用該方法對陣列進行恢復隨著陣列稀疏度和孔徑的增加對SNR和快拍數的要求也會更高，否則效果會較差。

B、基于奇異值閾值算法(Singular Value Thresholding, SVT)

這是一種數學上的矩陣恢復方法?基于稀疏陣列的回波數據信息去構造一個矩陣(該矩陣可以是Hankel矩陣、Toeplitz矩陣或者其它)，隨后基于SVT算法和一定的原則來補全這個構造的矩陣，從該補全后的矩陣來得到均勻陣列的信息。矩陣填充理論是一種重要的數據處理方式，假設矩陣滿足低秩性，但是矩陣的部分元素缺失導致信息不完整，矩陣填充理論通過利用已知信息，按照矩陣低秩的約束，來將缺失的信息補全。

關于使用Hankel矩陣+SVT算法的詳細說明和理解，可以參考Shunqiao Sun的相關論文，我在后文的參考文獻中給出了其中的兩篇。本小節的仿真也參考了其論文，這里給出基于Hankel和Toeplitz矩陣與SVT算法下的仿真結果對比。

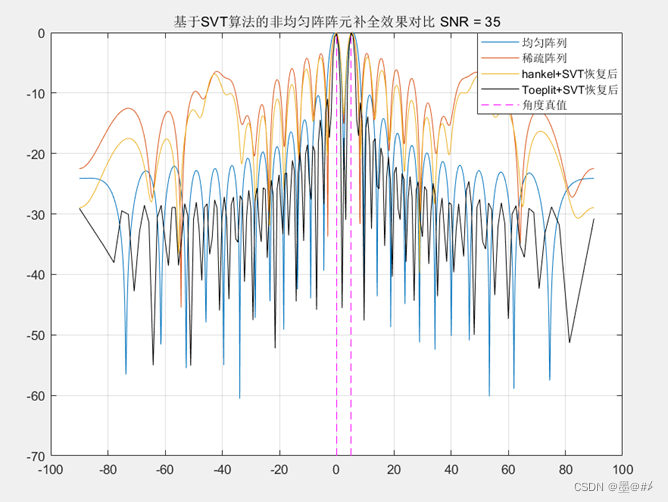
8陣元最小冗余陣[0 1 2 11 15 18 21 23]下補全前后的效果對比

目標在0°和5°的位置，基于Toeplitz方法恢復后的測角效果甚至優于均勻陣列，該方法用到了共軛信號？測角分辨率有一倍的提高？。基于Hankel矩陣的方法看起來效果不是很好，該方法的效果似乎與陣列的排布有很大的關系，且陣列孔徑越大該方法下的效果提升似乎會顯著一些，如下：

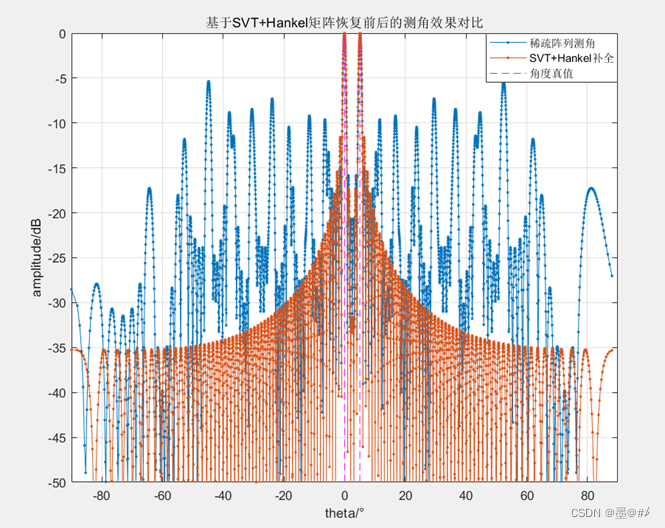
{[1 4 5 6 9 12 14 15 21 24 25 26 29 32 34 35 41 44 45 46 49 52 54 55 61 64 65 66 69 72 74 75 81 84 86 89 92 95 101 104 105 106 109 112 114 115]-1}該陣列下的陣元補全前后的測角效果對比

目標在0°和5°的位置，可以看到測角效果有明顯的提升。該陣列為前面提到的Sun的論文中給的陣列。

2.8一種“空間多快拍”的方法

測角的方法還有很多，但是各有要求以及優劣，能做工程應用的要少很多，能應用于車載的就更少了。本博文上面給出了比較經典和常見的幾種方法(或者也可以說是博主現階段有所積累的方法)的測角仿真效果以及各自的應用要求(對SNR和快拍數)，我會基于后續的學習和工作不定期更新一些較為有用且有意思的新算法。

2D-DOA估計方法討論

對于4D雷達，我們需要同時知道目標的水平和豎直向角度值以得到目標位置的準確測量。這便涉及到水平和豎直向角度的聯合估計問題。在前文第一章中對該問題做了簡單的敘述，本章對該問題進行詳述，并給出幾種角度匹配的方法。

1、無需進行角度匹配

類比我們對采集的ADC數據矩陣進行距離和速度維度的壓縮之后，通過檢測矩陣中的極值點(基于CFAR)，這些極值點的二維索引對應的就是該目標的距離和速度值。對于一個已知了距離和速度值的點(我們暫時還不知道滿足這個條件下有幾個目標)，我們將該點通道維度的數值按照實際的二維陣列排布得到一個數據矩陣，對該數據矩陣進行二維壓縮,通過檢測矩陣中的極值點，這些極值點的二維索引便對應了該目標的二維角度值。

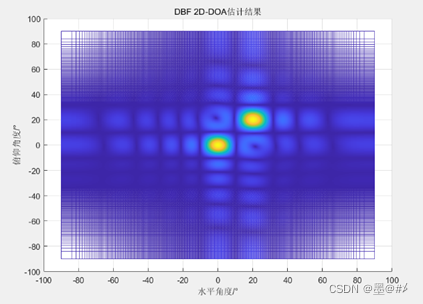
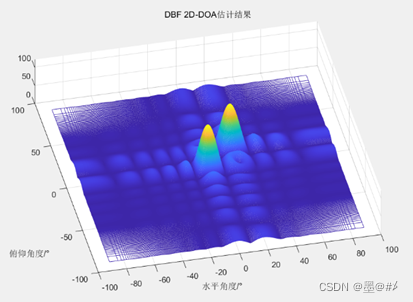
10*10的二維虛擬面陣仿真結果

目標在（0°，0°）、（20°，20°）的位置，可以看到當我們找到二維壓縮后的矩陣中的兩個極值點時，也就能直接得到該目標的二維角度值。不過在實際應用中，我們并不需要直接先二維壓縮之后再在該面陣中找極值點，而是先進行其中一個維度的壓縮，從這一維度的壓縮結果中得到目標在該維度的角度值，隨后只在有目標的索引值對應的行/列上進行另一維度的壓縮以完成目標的二維角度測量。

2、需要進行角度匹配

對于二維的矩形面陣，直接使用前面的方法是最優的，計算簡單，沒有復雜的匹配算法，信噪比和動態范圍都較高。但是從角度測量的角度來看，面陣其實有大量的信息冗余，我們其實并不需要一個完整的二維矩形面陣來得到目標的二維角度，我們可以很大程度上減少天線的使用，但是做任何事情都是有代價的，這樣做的代價是：需要設計更復雜的陣列以及需要用到更復雜的算法。

加特蘭在其baseband中提出了一種角度匹配思路，但是具體如何進行角度匹配的沒有做細節說明，下文給出一種類似的方法。為方便敘述和理解，我還是基于面陣來做說明。

如上圖所示，對于該二維矩形面陣，我們只要選取其中三列的數據來做目標的二維角度估計。對這三個group的數據分別使用FFT或者波束成形的方法對數據進行處理，可以使用找極值等方法得到目標可能的角度(三個角度group)，比如：Group1對應得到的角度為：α = （α1， α2， α3），Group2對應得到的角度為：β = (β1，β2，β3)，Group3對應的角度為：γ = (γ1，γ2，γ3)。α為三個目標水平方向的角度，β為三個目標豎直方向的角度，我們目前還無法確定它們之間的對應關系，但γ中包含了目標水平和豎直向的相關信息，我們可以基于如下關系完成α與β之間的匹配：

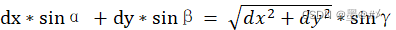
當選取斜對角線對應的陣元作為Group3時，上式中dx = dR1，dy = dR2。將三個group得到的角度信息代入上述關系式，便可以完成目標水平向和豎直向的角度匹配。

3、補充

二維角度關聯的方法有很多，比如還有陣列矩陣先向量化再進行角度估計等方法(博主這邊能跑通代碼但是原理理解得不是很深刻暫時不表)。需要進行角度關聯的操作時一般對陣列設計有一定的要求。

總結

本篇博文對毫米波雷達的DOA估計做了一個較為全面的概述，給出了包括DBF、FFT、Capon、Music、DML、ESPRIT、OMP、IAA等測角算法的基本介紹、仿真效果、以及應用的條件和對比。博文還探討了4D毫米波雷達的實現路線、2D-DOA估計方法等問題。2D-DOA估計部分收尾得有點倉促，前述DOA估計算法敘述得不算太詳細，囊括的DOA算法也不算太全，后面我會做一些豐富和更新。