Ising模型與QUBO模型
1.伊辛模型(Ising Model)
相干伊辛機(Coherent Ising Machine, 簡稱CIM), 是目前玻色量子重點研發(fā)的一項光量子計算機技術,CIM是一種基于簡并光學參量振蕩器(DOPO)的光量子計算機,在數(shù)學實踐中, 我們可以將其抽象為優(yōu)化Ising模型的專用計算機。
Ising模型是一類描述物質(zhì)相變的隨機過程模型。抽象為數(shù)學形式為:
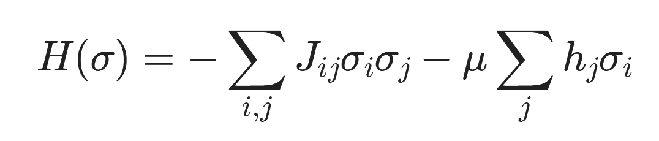
其中σ為待求自旋變量, 取值為{+1,-1},H為哈密頓量,J和μ分別為二次項系數(shù)、線性項系數(shù), 是已知量。
2.區(qū)分
QUBO模型更便于建模,Ising模型可以用于CIM求解器直接求解。同時,QUBO模型和Ising模型之間可以互相轉(zhuǎn)化。
1)變量代換
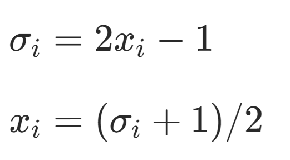
2)創(chuàng)建輔助變量完成一次項轉(zhuǎn)化
QUBO模型建模秘籍
一、什么是組合優(yōu)化問題?
組合優(yōu)化(Combinatorial Optimization, CO)領域是優(yōu)化領域中最重要的領域之一,它也是運籌學、計算機科學和分析學研究團體所追求的最活躍的研究領域之一。
組合優(yōu)化是在一個有限的對象集中找出最優(yōu)對象的一類問題。組合優(yōu)化的問題特征是可行解的集是離散或者可以簡化到離散的,目標是找到最優(yōu)解。常見的例子有數(shù)字劃分問題、旅行商問題等。
一般來說,這些問題涉及在必須做出大量是/否決策的情況下做出明智的選擇,并且每一組決策都會產(chǎn)生相應的目標函數(shù)值,例如成本或利潤值。然而在這些環(huán)境中找到好的解決方案是極其困難的。
而QUBO建模方式可以包含在工業(yè)、科學和政府中發(fā)現(xiàn)的各種重要CO問題,借助QUBO求解器的求解能力可以有效地幫助解決許多重要問題。
二、什么是QUBO模型?
QUBO(QuadraticUnconstrained Binary Optimizatoin),無約束二次二進制優(yōu)化模型是現(xiàn)在量子計算中應用最廣泛的優(yōu)化模型,它統(tǒng)一了豐富多樣的組合優(yōu)化問題。
隨著問題規(guī)模的增加,利用傳統(tǒng)方法求解該問題,求解時間會變得不可接受,但利用QUBO模型可以通過量子計算機加速,高效求解組合優(yōu)化問題。同時,QUBO模型可以表達位運算,進而表達各種邏輯,操作簡便,具體形式如下。
1.基礎QUBO形式:minimize/maximize
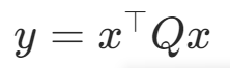
Q為QUBO矩陣,x為二進制變量組成的向量,每個變量取值均為{0,1},QUBO目標為找到使得y最小或最大的x
其中,Q矩陣的形式有2種:
1)對稱形式
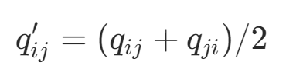
2)上三角形式
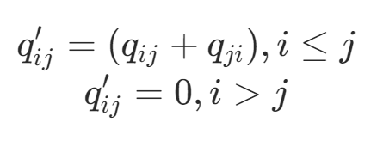
舉例:
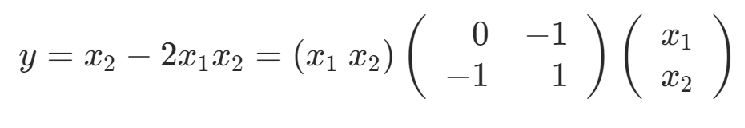
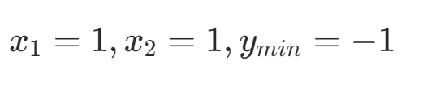
2.位運算
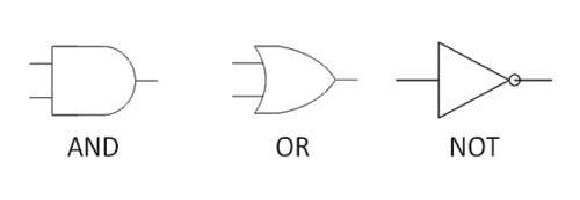
與 同時為1,結(jié)果才為1;
或 同時為0,結(jié)果才為0;
非0變成1,1變成0;
異或 兩位相同為0,相異為1
位運算表達
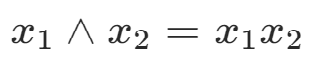
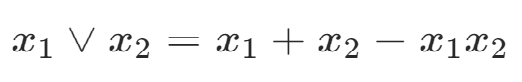
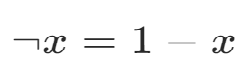
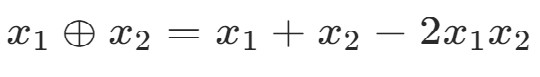
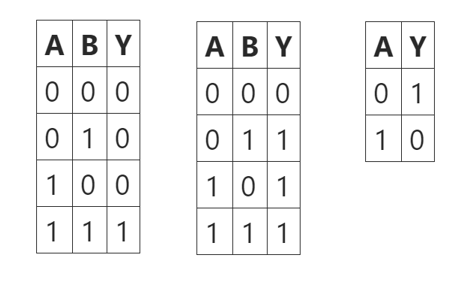
3.添加約束條件
舉例1:
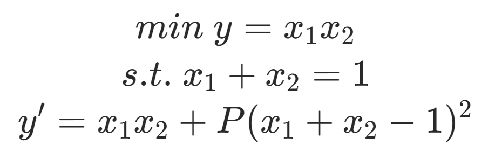
通過添加約束項,并設置較大的系數(shù)P保證約束內(nèi)容的優(yōu)先級。
舉例2:
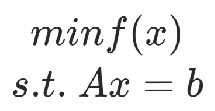
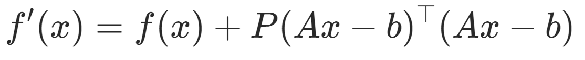
約束條件舉例
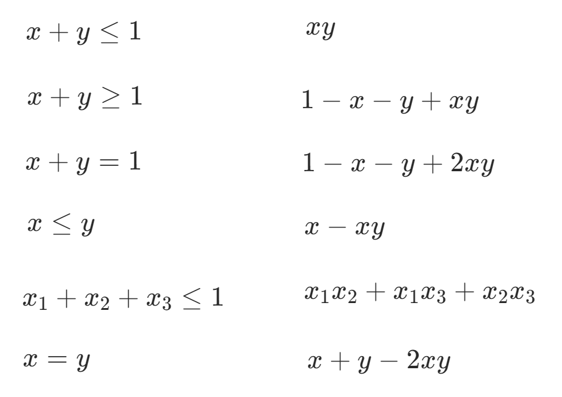 ? ? ?
? ? ?
4.整數(shù)表達
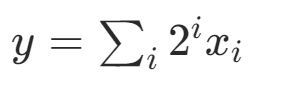
通過二進制表達整數(shù),使用d個變量可以表達0到2^d ?1 的數(shù)字。
舉例:
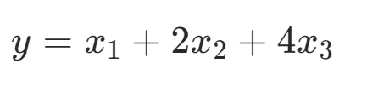
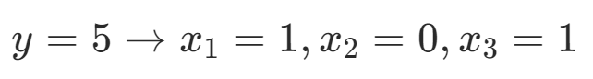
5.不等式約束
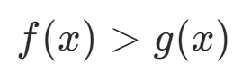
不等式約束可以轉(zhuǎn)化為等式約束,通過松弛變量y表示出不等式兩邊的差。
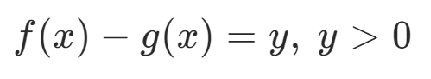
其中y為通過二進制表達的整數(shù),構(gòu)造約束項:
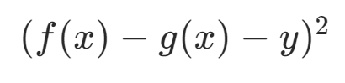
(注意點:這樣做會引入新的變量,增加問題規(guī)模)
6.擴展思考
HOBO問題(High Order Binary Optimization),是指用二次多項式難以表達的高次問題。對于高次的問題,可以將x1x2替換為y,并添加約束項使得x1x2=y,從而將高次的問題轉(zhuǎn)化為二次優(yōu)化問題。
約束項:Rosenberg多項式
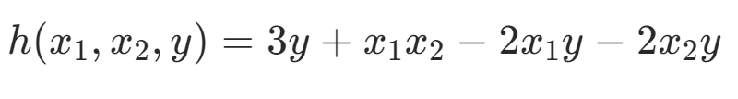
滿足:
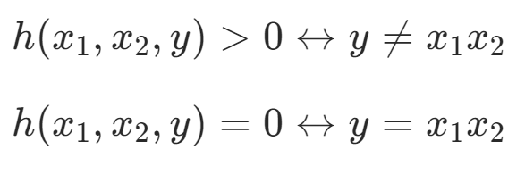
(注意點:這樣做會引入新的變量,增加問題規(guī)模)
三、QUBO可以解決哪些問題?
最大獨立集問題
不對稱分配問題
對稱分配問題
邊約束分配問題
二次背包問題
最大團問題
最大割問題
整數(shù)劃分問題
旅行商問題
舉例1:整數(shù)劃分問題
1)整數(shù)劃分問題(The Number Partitioning Problem),NP-complete將包含n個非負整數(shù)的數(shù)集劃分為兩個子集,使這兩個子集的和盡可能接近
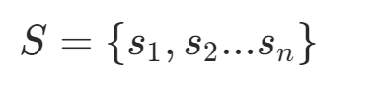
設數(shù)集為
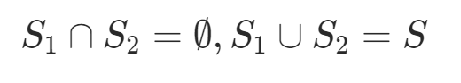
選兩個子集滿足,使得下值最小
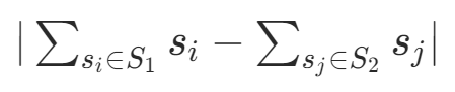
舉例S= {1,2,3,4,8},一組最有解為S1= {1,8} S2={2,3,4}是一組最優(yōu)解,兩者的和均為9
2)整數(shù)劃分問題建模思路
1. 定義決策變量,決定每個整數(shù)被分到哪一個集合
2. 使用決策變量表達出兩個集合整數(shù)和的差值
3. 通過CIM優(yōu)化目標函數(shù),得到最小值對應的解
3)整數(shù)劃分問題建模過程
定義決策變量xi,xi=1表示 Si∈S1,xi=0表示Si∈S2
兩個子集求和的差值:
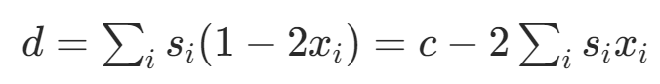
目標函數(shù):
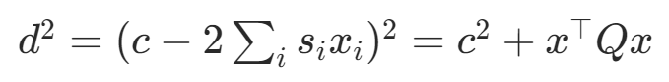
其中,
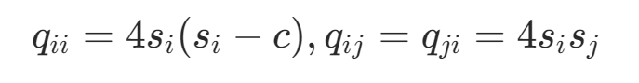
舉例2:旅行商問題
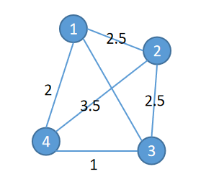
1)旅行商問題(Traveling Salesman Problem)NP-Complete,商人想要在地圖上走完所有城市,每個城市只經(jīng)過一次,最后回到最初的城市,求路程最短的走法。
給定帶權圖G(V,E),V為點集,E為邊集,要求遍歷所有點再回到初始點,求路程最短的走法。哈密頓回路:遍歷所有點再回到初始點。
舉例:

2)旅行商問題建模思路1.0
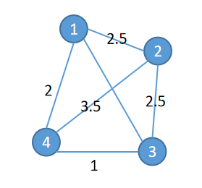
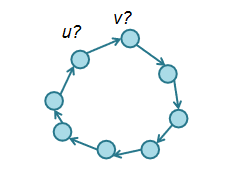
以下圖為例,定義決策變量xi,u,表示“經(jīng)過的第i個節(jié)點為u”是否為真,通過決策變量表達出距離,再通過添加約束條件使得求解方案能夠成立,構(gòu)造得到表達式通過CIM進行優(yōu)化。
目標包括:
1. 路程最小
2. 路線為環(huán)(約束自然滿足)
3. 同時只能經(jīng)過一個節(jié)點(約束)
4. 每個點經(jīng)過次數(shù)為1(約束)
5. 不能走不存在的連接(約束)
3)旅行商問題建模過程
設有n個節(jié)點,wu,v從u到v的邊的邊權,定義決策變量xi,u,表示“經(jīng)過的第i個節(jié)點為u”是否為真,路程為環(huán)可以根據(jù)決策變量的定義自然滿足,則經(jīng)過的路程可以表達為:
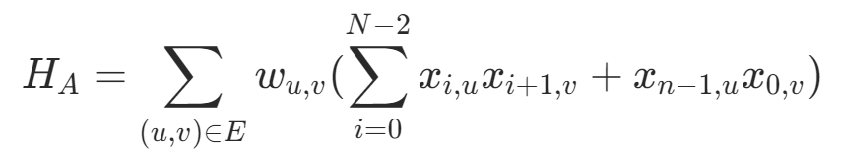
4)旅行商問題約束條件
為使得xi,u符合實際情況,需要如下約束:
第i個節(jié)點只有一個節(jié)點
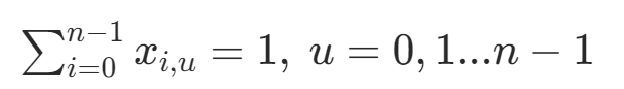
節(jié)點u只在路線中出現(xiàn)一次
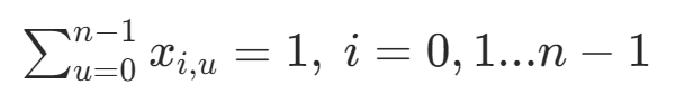
可以根據(jù)以上兩個條件構(gòu)造約束
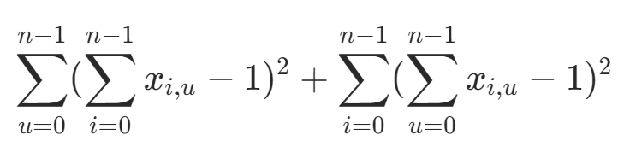
為了保證不存在的邊不出現(xiàn)在方案中設置約束項
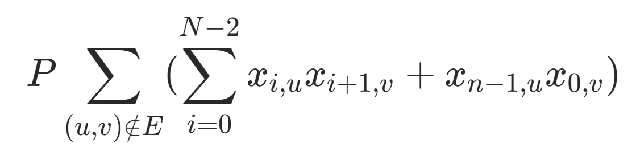
P為懲罰項系數(shù),取值需要顯著大于其他邊權,最終的約束項:
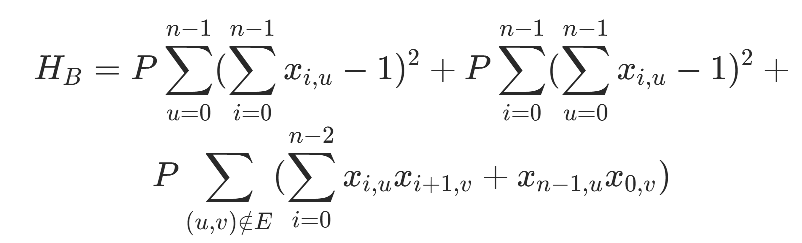
目標函數(shù)包括回路總長和約束兩部分:
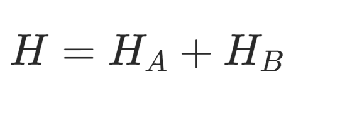
2)旅行商問題建模思路2.0
定義決策變量xu,v,表示“使用u到v的邊”,通過決策變量表達出距離,再通過添加約束條件使得求解方案能夠成立,構(gòu)造得到表達式通過CIM進行優(yōu)化。
目標包括:
1. 路程最小
2. 每個點出發(fā)一次(約束)
3. 到達每個點一次(約束)
4. 不能走不存在的連接(約束)
由于相干光量子計算最擅長攻克組合優(yōu)化問題,可應用賦能場景廣泛,如金融業(yè)的投資組合優(yōu)化、資本風險分析建模;生物制藥業(yè)的蛋白質(zhì)折疊、小分子組合和DNA重組;
交通物流行業(yè)路徑優(yōu)化等,這些都是在實際工作中經(jīng)常遇見的復雜度很高且計算量巨大的常規(guī)問題,所以該技術路線高度貼合市場需求,普適率高。
審核編輯:劉清
-
CIM
+關注
關注
1文章
88瀏覽量
15613 -
求解器
+關注
關注
0文章
79瀏覽量
4724 -
光量子計算機
+關注
關注
0文章
11瀏覽量
1736
原文標題:玻色量子真機體驗|一文了解如何應用QUBO模型來建模
文章出處:【微信號:玻色量子,微信公眾號:玻色量子】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄



















評論