3.插入

往數組里插入一個新元素的速度，取決于你想把它插入到哪個位置上。

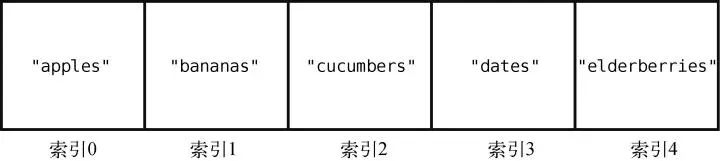
假設我們想要在購物清單的末尾插入"figs"。那么只需一步。因為之前說過了，計算機知道數組開頭的內存地址，也知道數組包含多少個元素，所以可以算出要插入的內存地址，然后一步跳到那里插入就行了。圖示如下。

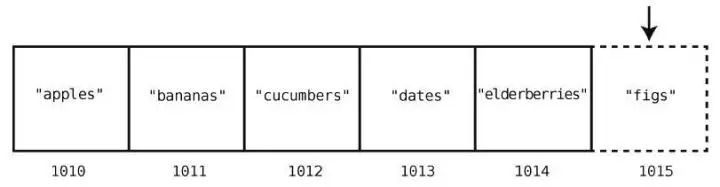
但在數組開頭或中間插入，就另當別論了。這種情況下，我們需要移動其他元素以騰出空間，于是得花費額外的步數。

例如往索引2 處插入"figs"，如下所示。

為了達到目的，我們必須先把"cucumbers"、"dates"和"elderberries"往右移，以便空出索引2。而這也不是一步就能移好，因為我們首先要將"elderberries"右移一格，以空出位置給"dates"，然后再將"dates"右移，以空出位置給"cucumbers"，下面來演示這個過程。

第1 步："elderberries"右移。

第2 步："date"右移。

第3 步："cucembers"右移。

第4 步：至此，可以在索引2 處插入"figs"了。

如上所示，整個過程有4 步，開始3 步都是在移動數據，剩下1 步才是真正的插入數據。

最低效（花費最多步數）的插入是插入在數組開頭。因為這時候需要把數組所有的元素都往右移。于是，一個含有N 個元素的數組，其插入數據的最壞情況會花費N + 1 步。即插入在數組開頭，導致N 次移動，加上一次插入。

最后要說的“刪除”，則相當于插入的反向操作。

4.刪除

數組的刪除就是消掉其某個索引上的數據。

我們找回最開始的那個數組，刪除索引2 上的值，即"cucumbers"。

第1 步：刪除"cucumbers"。

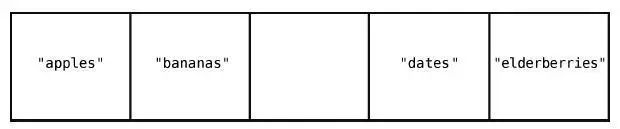
雖然刪除"cucumbers"好像一步就搞定了，但這帶來了新的問題：數組中間空出了一個格子。因為數組中間是不應該有空格的，所以，我們得把"dates"和"elderberries"往左移。

第2 步：將"dates"左移。

第3 步：將"elderberries"左移。

結果，整個刪除操作花了3 步。其中第1 步是真正的刪除，剩下的2 步是移數據去填空格。

所以，刪除本身只需要1 步，但接下來需要額外的步驟將數據左移以填補刪除所帶來的空隙。

跟插入一樣，刪除的最壞情況就是刪掉數組的第一個元素。因為數組不允許空元素，當索引0 空出，那么剩下的所有元素都要往左移去填空。

對于含有5 個元素的數組，刪除第一個元素需要1 步，左移剩余的元素需要4 步。而對于500個元素的數組，刪除第一個元素需要1 步，左移剩余的元素需要499 步。可以推出，對于含有N個元素的數組，刪除操作最多需要N 步。

既然學會了如何分析數據結構的時間復雜度，那就可以開始探索各種數據結構的性能差異了。了解這些非常重要，因為數據結構的性能差異會直接造成程序的性能差異。

下一個要介紹的數據結構是集合，它跟數組似乎很像，甚至讓人以為就是同一種東西。然而，我們將會看到它跟數組在性能上是有區別的。

集合：一條規則決定性能

來看看另一種數據結構：集合。它是一種不允許元素重復的數據結構。

其實集合是有不同形式的，但現在我們只討論基于數組的那種。這種集合跟數組差不多，都是一個普通的元素列表，唯一的區別在于，集合不允許插入重復的值。

要是你想往集合["a", "b", "c"]再插入一個"b"，計算機是不會允許的，因為集合中已經有"b"了。

集合就是用于確保數據不重復。

如果你要創建一個線上電話本，你應該不會希望相同的號碼出現兩次吧。事實上，現在我的本地電話本就有這種狀況：我家的電話號碼不單指向我這里，還錯誤地指向了一個叫Zirkind 的家庭（這是真的）。接聽那些要找Zirkind 的電話或留言真的挺煩的。

不過，估計Zirkind 一家也在納悶為什么總是接不到電話。而當我想要打電話告訴Zirkind 號碼錯了的時候，我妻子就會去接電話了，因為我撥的就是我家號碼（好吧，這是開玩笑）。如果這個電話本程序用集合來處理，那就不會搞出這種麻煩了。

總之，集合就是一個帶有“不允許重復”這種簡單限制的數組。而該限制也導致它在4 種基本操作中有1 種與數組性能不同。

下面就來分析讀取、查找、插入和刪除在基于數組的集合上表現如何。

集合的讀取跟數組的讀取完全一樣，計算機只要一步就能獲取指定索引上的值。如之前解釋的那樣，這是因為計算機知道集合開頭的內存地址，所以能夠一步跳到集合的任意索引。

集合的查找也跟數組的查找無異，需要N 步去檢查某個值在不在集合當中。刪除也是，總共需要N 步去刪除和左移填空。

但插入就不同了。先看看在集合末尾的插入。對于數組來說，末尾插入是最高效的，它只需要1 步。

而對于集合，計算機得先確定要插入的值不存在于其中——因為這就是集合：不允許重復值。

于是每次插入都要先來一次查找。

假設我們的購物清單是一個集合——用集合還是不錯的，畢竟你不會想買重復的東西。如果當前集合是["apples", "bananas", "cucumbers", "dates", "elderberries"]，然后想插入"figs"，那么就需要做一次如下的查找。

第1 步：檢查索引0 有沒有"figs"。

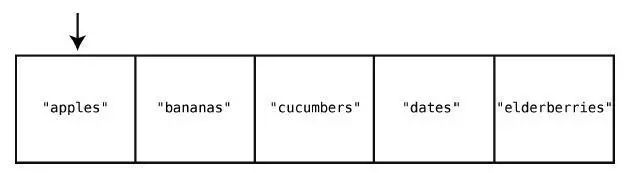
沒有，不過說不定其他索引會有。為了在真正插入前確保它不存在于任何索引上，我們繼續。

第2 步：檢查索引1。

第3 步：檢查索引2。

第4 步：檢查索引3。

第5 步：檢查索引4。

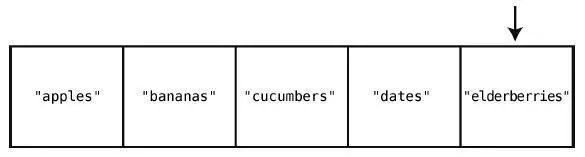
直到檢查完整個集合，才能確定插入"figs"是安全的。于是，到最后一步。

第6 步：在集合末尾插入"figs"。

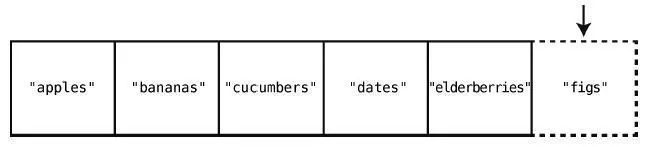
在集合的末尾插入也屬于最好的情況，不過對于一個含有5 個元素的集合，你仍然要花6 步。因為，在最終插入的那一步之前，要把5 個元素都檢查一遍。

換句話說，在N 個元素的集合中進行插入的最好情況需要N + 1 步——N 步去確認被插入的值不在集合中，加上最后插入的1 步。

最壞的情況則是在集合的開頭插入，這時計算機得檢查N 個格子以保證集合不包含那個值，然后用N 步來把所有值右移，最后再用1 步來插入新值。總共2N + 1 步。

這是否意味著因為它的插入比一般的數組慢，所以就不要用了呢？當然不是。在需要保證數據不重復的場景中，集合是非常重要的（真希望有一天我的電話本能恢復正常）。但如果沒有這種需求，那么選擇插入比集合快的數組會更好一些。具體哪種數據結構更合適，當然要根據你的實際應用場景而定。

總結

理解數據結構的性能，關鍵在于分析操作所需的步數。采取哪種數據結構將決定你的程序是能夠承受住壓力，還是崩潰。本文特別講解了如何通過步數分析來判斷某種應用該選擇數組還是集合。