繞組是電和磁的橋梁,匝鏈繞組的磁通發(fā)生變化時,繞組中就產(chǎn)生感應電勢;反過來繞組中通以電流時,就會產(chǎn)生磁場,因此電機繞組的核心作用就是產(chǎn)生感應電勢和磁勢,電勢和磁勢是反映繞組電磁特性的兩個方面,二者雖然物理意義不同,但分析時具有相同的數(shù)學形式,存在著許多內(nèi)在的共性,從電勢觀點所得出的某些分析結論,往往可以直接用于磁勢的分析。接下來我們將分幾期來分別介紹繞組產(chǎn)生的電勢和磁勢,揭示它們之間的內(nèi)在聯(lián)系和共性規(guī)律,本期先從繞組的感應電勢講起。表征繞組中感應電勢的物理量包括電勢的大小(幅值、有效值)、波形、頻率以及相位等,這些都與氣隙磁場的大小、轉(zhuǎn)速、波形、初始位置等密切相關,本期先講正弦磁場下繞組的電勢,即基波感應電勢。首先從單根導體的感應電勢開始,推導出單匝線圈的感應電勢,再根據(jù)線圈的連接關系進一步推導出線圈組的電勢,進而得出相電勢和三相繞組的電勢。
1 單根導體產(chǎn)生的基波電勢
1.1 基波感應電勢的波形
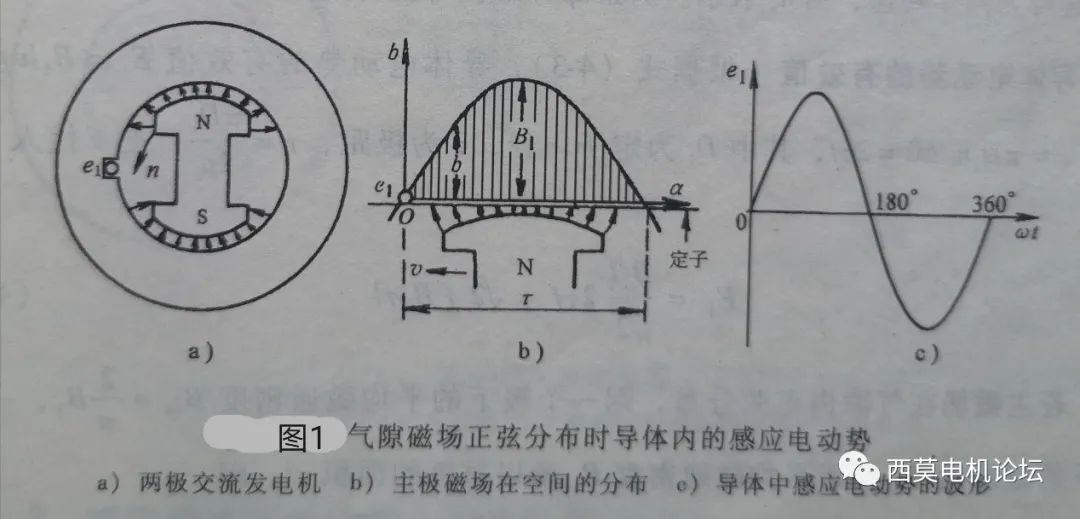
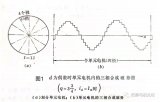
如圖1所示,為一臺兩極同步電機示意圖,定子表面只有一個槽,槽內(nèi)嵌放一根導體。
 ?
?
當氣隙磁場旋轉(zhuǎn)時,導體便“切割”氣隙磁場,產(chǎn)生感應電勢。設氣隙磁密為正弦分布:
b=B1?sinα (1)
式中:B1為氣隙磁密幅值;α為距離原點的電角度,原點位置取兩極中間的分界點。
設t=0時α=0,即導體初始位置位于兩極分界點,則隨著磁極以角速度ω旋轉(zhuǎn),α=ωt,則導體中的基波感應電勢即為:
e1=blv=B1lv?sinωt=2^??E1?sinωt (2)
式中:E1=B1lv/2^?為導體感應電勢的有效值;l為導體的有效長度;v為導體“切割”磁力線的速度。由⑴、⑵式可見,若氣隙磁密呈正弦分布,以恒定轉(zhuǎn)速旋轉(zhuǎn)時,則定子導體中的感應電勢就是隨時間呈正弦變化的交流電勢,感應電勢隨時間變化的波形如圖1c所示。
1.2 基波感應電勢的頻率
如圖1所示兩極電機(極對數(shù)p=1)轉(zhuǎn)子每旋轉(zhuǎn)一周,導體中的感應電勢就交變一次,若電機為p對極,則轉(zhuǎn)子每旋轉(zhuǎn)一周,導體中的感應電勢就交變p次,設轉(zhuǎn)子轉(zhuǎn)速為n(轉(zhuǎn)/分鐘),則感應電勢的頻率即為:
f=pn/60 (3)
由⑶式可見,感應電勢的頻率與電機的極對數(shù)和轉(zhuǎn)速密切相關,式中的n被稱為同步轉(zhuǎn)速,常用n1或ns表示。
1.3 單根導體感應電勢的大小
由⑵式可知,單根導體的感應電勢有效值為:
E1=B1lv/2^?(4)
其中線速度:
v=π?Di?n/60=2τf (5)
式中:Di為定子內(nèi)徑;τ=πDi/(2p)為極距。
將⑸式代入⑷式得:
E1=B1?l?(2τf)/2^?=(2^?)?f?B1?τ?l (6)
若氣隙磁密為正弦分布,則磁密的平均值為:
Bav=(1/π)∫【0~π】B1sinα?dα=(2/π)?B1(7)
B1=(π/2)?Bav(8)
將⑻式代入⑹式得:
E1=(2^?)?f?(π/2)(Bav?τ?l)=2.22?f?Φ1 (9)
式中:Φ1=Bav?τ?l,為每極磁通(Wb)。
2 單個線圈的基波電勢
2.1 整距線圈的電勢
一個單匝線圈由兩根導體反向串聯(lián)組成,由于兩根導體的電勢都是隨時間正弦變化,因此可以用相量來進行和運算。設兩個導體的電勢相量分別為E1′和E1″,則這個單匝線圈的電勢即為:
Ec1=E1′-E1″ (10)
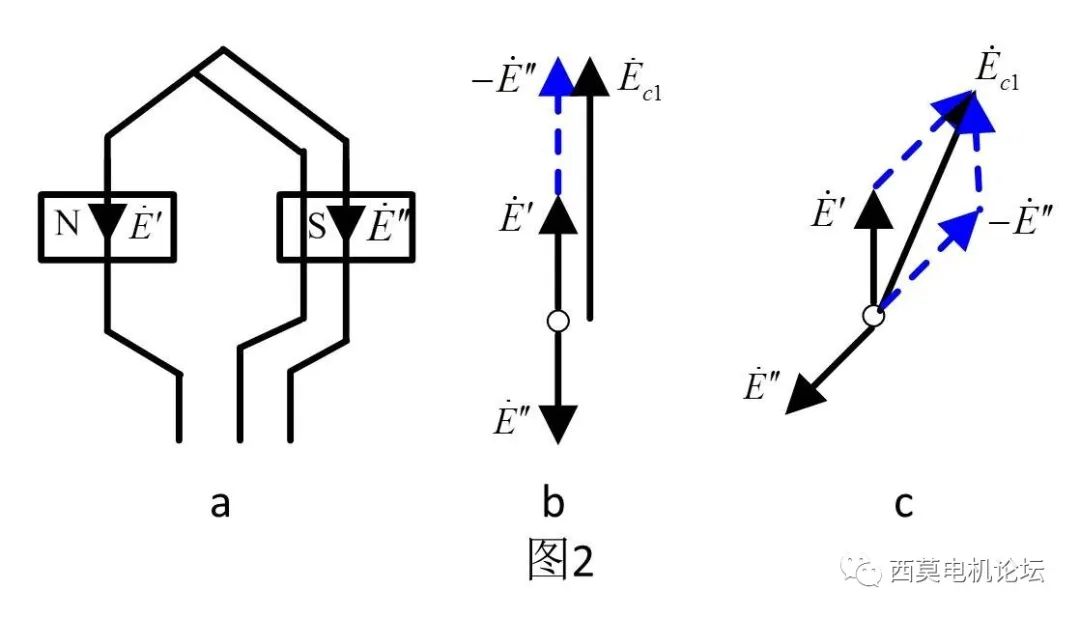
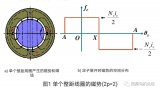
對于整距線圈,當一根導體位于N極中心線時,另一個導體必然位于S極的中心線處,如圖2所示,兩個導體的感應電勢相位正好相反,即E1′=-E1″,二者反向串聯(lián)后得到單匝線圈的感應電勢即為:
Ec1(整距)=E1′-E1″=2E1′=4.44?f?Φ1 (11)
如果線圈的匝數(shù)為W,則線圈的電勢即為:
Ec1(整距)=4.44?f?W?Φ1 (12)
這就是傳說中的“4.44公式”,它是電機學里的經(jīng)典公式,搞電機的同學們應該對它爛熟于心。
以上是從“Blv”觀點出發(fā)推導出的這個公式,這個公式還可以通過“e=-W?dΦ/dt”的觀點推出。設t=0時整距線圈的兩個邊分別位于NS極的分割線上,此時匝鏈線圈的磁通最大,為Φ1 ,若氣隙磁場為正弦分布,隨著氣隙磁場的旋轉(zhuǎn),匝鏈線圈的磁通將隨時間呈余弦變化,即:
Φ=Φ1 ?cosωt (13)
則線圈的感應電勢:
e=-W?dΦ/dt=-W?ω?Φ1 ?(-sinωt)=W?2πf?Φ1 ?sinωt (14)
其有效值為:
Ec1(整距)=f?W?Φ1 ?(2π/2^?)=4.44?f?W?Φ1 (15)
由(12)和(15)可見,用“Blv”觀點和“e=-W?dΦ/dt”觀點推導出了同樣的結論。
順便解釋一個許多同學糾結的問題,有人覺得“Blv”觀點是錯誤的,因為通常導體是嵌放在鐵心槽里的,而槽內(nèi)的磁場B幾乎為0,用這個觀點推導出感應電勢也應該是幾乎為0。關于這個問題可以這樣理解:首先“Blv”觀點來自初中物理中導體“切割磁力線”產(chǎn)生感應電勢這個知識點,由于在初中階段的數(shù)學知識所限,不大可能用電磁場的概念和相關數(shù)學模型去解釋物理現(xiàn)象,建立非常精確的理論體系,只能用初等數(shù)學的知識來描述電磁感應現(xiàn)象,因此在初中階段“Blv”觀點可以完美地解釋和描述導體在勻強磁場下做切割磁力線運動產(chǎn)生感應電勢這種非常簡單場合下的物理規(guī)律。對于像電機中這樣復雜的電磁場問題,再用“Blv”觀點去精確推導一些結論的確存在一些瑕疵,應該采用更加精確的電磁場數(shù)學模型——麥克斯韋方程組來推導,即采用“e=-W?dΦ/dt”觀點計算感應電勢更加確切。雖然“Blv”觀點有瑕疵,但瑕不掩瑜,既然“Blv”觀點推導過程中,B采用的是氣隙磁密,而不是槽內(nèi)磁場的磁密,卻得出了用“e=-W?dΦ/dt”觀點推導同樣的結論,那你就認為“Blv”觀點中的B代表氣隙磁密,就不要鉆牛角尖非得糾結這個B不是槽內(nèi)磁密了!如果你一定要較勁,認為“Blv”中的B就應該是槽內(nèi)磁密,OK!那我們就死磕到底,如果這里的B是槽內(nèi)磁密,那么這里的v就必須得是槽內(nèi)導體切割磁力線的速度,而不能是氣隙旋轉(zhuǎn)磁場的線速度,那么槽內(nèi)導體切割磁力線的速度該怎么算呢?我們說槽內(nèi)導體“切割磁力線”,是指一開始磁力線集中在這個槽的一側(cè)的齒中(假設右側(cè)齒中),然后在極短的時間內(nèi)快速“跳變”到槽的另一側(cè)(左側(cè))齒中,我們把這個過程稱為槽內(nèi)導體“切割了磁力線”,這個過程極其短暫以致于幾乎不用時間,也就是說,切割磁力線的速度是接近無窮大,這樣槽內(nèi)的磁密B趨近于0,而切割磁力線的速度v卻趨近于無窮大,一個無窮小和一個無窮大相乘并不一定是0,那應該是多少呢?告訴你經(jīng)過嚴謹?shù)目茖W推導,二者的乘積就等于氣隙磁密與旋轉(zhuǎn)磁場的線速度的乘積,考慮到同學們的數(shù)學基礎和篇幅所限,這里就不詳細推導了,只需你記住一點,就是用“Blv”觀點推導時,其中的B要用氣隙磁密,而不是用槽內(nèi)磁密即可,如果非得較勁,我們也能跟您死磕到底!
2.2 非整距線圈的基波電勢
若線圈不是整距線圈,即短距Y1<τ(或長距Y1>τ),則一個線圈中的兩個導體產(chǎn)生的感應電勢相位就不是正好反相位,而是相差了γ=(Y1/τ)?180o的電角度,如圖2c所示,此時線圈的電勢就不應該是兩根導體電勢E1′和-E″的代數(shù)和,而是二者的相量和,以短距線圈為例:
Ec1(短距)=E1′∠0o-E1″∠γ=2E1′? sin[(Y1/τ)?90o]=4.44?Kp1?f?Φ1 (16)
若線圈的匝數(shù)為W,則單個線圈的電勢為:
Ec1(短距)=4.44?Kp1?W?f?Φ1 =Kp1?Ec1(整距)(17)
式中:Kp1稱為線圈的基波短距系數(shù),其物理意義是線圈短距時由于兩根導體的電勢不是正好反相位,二者相量疊加后的線圈電勢大小就不會等于整距線圈的電勢(單根導體電勢的2倍),而是略小于整距線圈的電勢,相當于短距線圈的電勢在整距線圈電勢基礎上打了一個折扣,這個折扣就是Kp1。
Kp1=Ec1(短距)/Ec1(整距)=sin[(Y1/τ)?90o] (18)
顯然對于整距線圈Kp1=1;對于短距線圈Kp1<1,以上推導同樣適用于長距線圈,說明非整距線圈的電勢必須在整距線圈電勢基礎上打個折扣。
3 線圈組的基波合成電勢
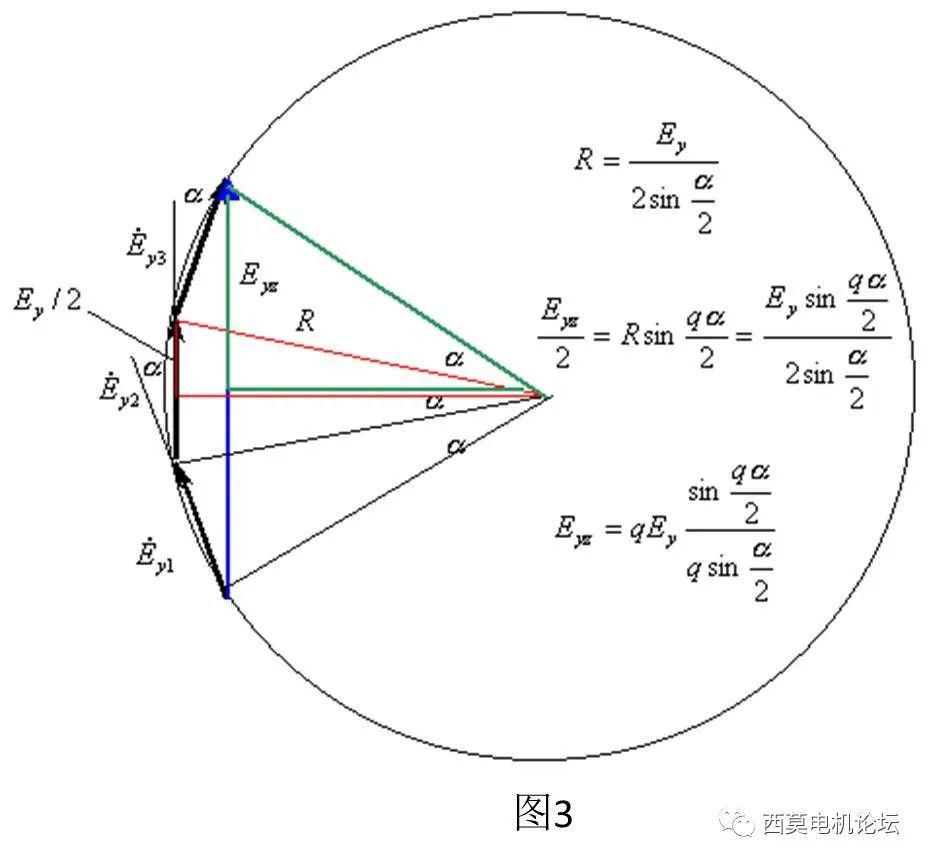
若q個分布線圈串聯(lián)構成一個線圈組(極相組),則由于線圈分布,每個線圈的電勢并非同相位,而是相鄰兩個線圈電勢相差α電角度,因此這q個分布線圈串聯(lián)后的合成電勢并不是單個線圈電勢的q倍,而是必然在q倍的基礎上再打一個分布系數(shù)Kd1的折扣,如圖3所示,即:
Eq1=Ey1∠0o+Ey1∠α+Ey1∠2α+…+Ey1∠(q-1)α
=q?Kd1?Ec1(短距)=4.44q?Kd1?Kp1?W?f?Φ1
=4.44q?Kdp1?W?f?Φ1 =4.44?Kdp1?(qW)?f?Φ1 (19)
式中:
Kd1=[sin(q?α/2)]/[q?sin(α/2)](20)
其中:W為單個線圈的匝數(shù);α為串聯(lián)線圈中兩個相鄰分布線圈電勢之間的相位差。
α=t?360o/Z1(21)
其中:t為單元電機個數(shù);Z1為定子總槽數(shù)。對于整數(shù)槽繞組(t=p),α即為槽距角,則將式(21)中的t用極對數(shù)p取代即可;對于分數(shù)槽繞組,則α應為串聯(lián)線圈組間的相位差,應從槽電勢星型圖中求取,這里又分兩種情況:若q的分母d為奇數(shù),則直接用式(21)計算α即可,即α為槽電勢星型圖中兩根相鄰相量間的相位差;若d為偶數(shù),則α應取式(21)計算出的α的一半,即按下式計算:
α=t?180o/Z1 (22)
詳見本系列文章之電機繞組(四)中的α′(對d為奇數(shù)的情況)或α′/2(對d為偶數(shù)的情況)。
Kdp1=Kd1?Kp1 (21)
稱為基波繞組系數(shù),即短距系數(shù)與分布系數(shù)的乘積,相當于短距分布繞組的感應電勢應該在整距集中線圈基礎上打一個短距系數(shù)折扣,再打一個分布系數(shù)折扣后的總折扣系數(shù)。
4 相繞組的基波電勢
如果多個線圈組通過串并聯(lián)組成一相繞組,那么該相繞組的感應電勢取決于該相繞組的總串聯(lián)匝數(shù)W,相繞組的基波感應電勢為:
EΦ1=4.44?f?Kdp1?W?Φ1 (22)
再次強調(diào)!式中的W為每相串聯(lián)匝數(shù),即一條支路中所有線圈的總匝數(shù)。
5 三相繞組的基波感應電勢
根據(jù)繞組的接法不同,計算三相繞組的線電勢。如果是Y接,則三相繞組的線電勢為相電勢的根號三倍;如果是Δ接,則三相繞組的線電勢與相電勢相等。
6 感應電勢與磁鏈的相位關系
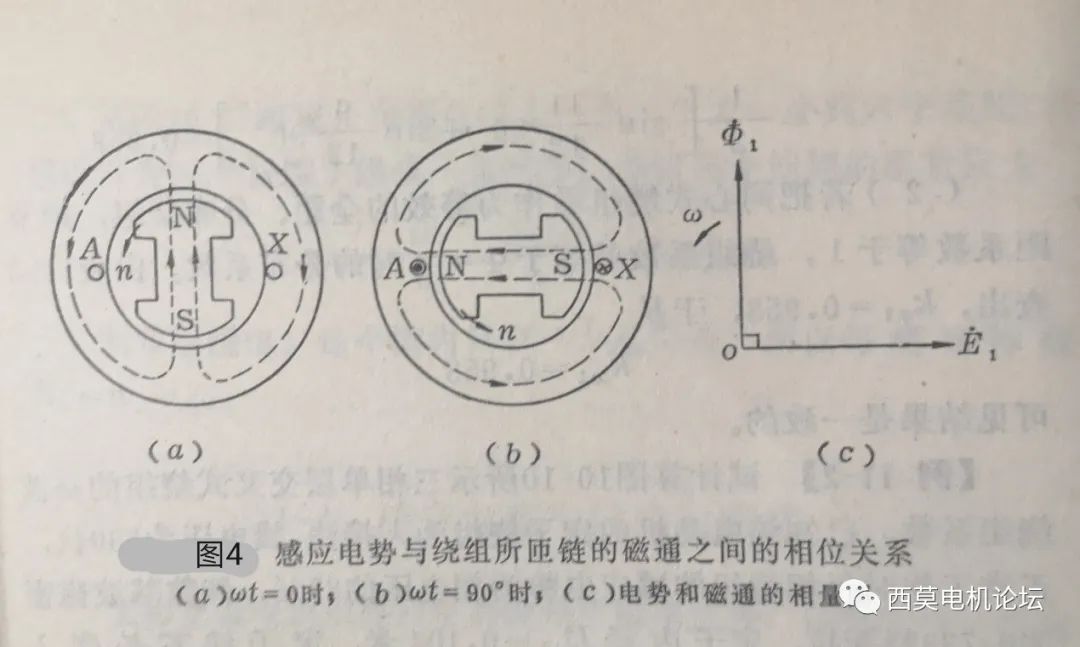
通常在畫電機的時空相量圖時,還需要搞明白感應電勢和氣隙磁場間的相位關系。根據(jù)e=-W?dΦ/dt,可知e與Φ之間的相位關系是:感應電勢e滯后繞組所匝鏈磁通Φ90o相位。需要說明的是,這里的Φ是指匝鏈繞組的磁通,它是隨時間呈正弦變化的物理量,即e和Φ都是時間的正弦函數(shù),即隨著氣隙磁場的旋轉(zhuǎn),匝鏈繞組的磁通也隨時間呈正弦變化,但在電機中,匝鏈繞組的磁通是一個幅值不變、大小隨空間呈正弦變化的旋轉(zhuǎn)磁場,在旋轉(zhuǎn)過程中引起的匝鏈繞組磁通隨時間呈正弦變化的,從這個角度看,Φ也可看著是一個空間矢量,隨著它旋轉(zhuǎn),引起了繞組的匝鏈磁通隨時間變化,在電機的時空相量圖中,往往要把隨時間變化的時間相量和隨空間變化的空間矢量統(tǒng)一畫到一起。設在一開始(t=0時刻)旋轉(zhuǎn)磁場的中心與繞組的軸線對齊,如圖4a所示,則此時與繞組匝鏈的磁通Φ1最大,但由于此時繞組的兩條邊正好位于磁場為0的位置,因此,此時繞組的感應電勢e=0,當磁場旋轉(zhuǎn)過90o電角度時,即磁場中心線與繞組軸線成90o時,此時繞組匝鏈的磁通為0,但此時由于繞組的兩條邊正好位于磁密最大處,繞組的感應電勢卻最大,如圖4b所示,由此可見當繞組匝鏈的磁通為最大時,繞組的感應電勢為0;而當磁場旋轉(zhuǎn)過90o電角度(ωt=90o)時,繞組匝鏈的磁通為0,但繞組的感應電勢卻達到最大,因此如果把Φ1看作繞組所匝鏈磁通,則Φ1即為時間相量,在時間上看,繞組感應電勢在時間上滯后所匝鏈磁通90o;如果把Φ1看著旋轉(zhuǎn)磁場的最大磁通量,則Φ1即為空間矢量,那么從空間上看,繞組感應電勢在空間上同樣滯后旋轉(zhuǎn)磁場90o的空間電角度。因此在畫電機時空相量圖時,無論把Φ1看著時間相量還是空間矢量,都可以把感應電勢畫在滯后磁通90o的位置,如圖4c所示。
 ?
?
以上分析,僅是當氣隙磁場呈正弦分布時繞組的感應電勢,或者說是在任意氣隙磁場下繞組的基波感應電勢,本文分析了基波感應電勢的頻率、相位和大小,并重點分析了感應電勢大小的計算方法。對于實際電機而言,氣隙磁場中除了基波磁場以外,往往還存在著許多諧波磁場,即氣隙磁場往往并不是嚴格呈正弦分布,這樣就會在繞組中產(chǎn)生一系列諧波電勢,關于繞組感應電勢的諧波分析會更加復雜,如果您對李老師的文章還意猶未盡,歡迎5月27日-29日來無錫參加“電機NVH問題的機理及測試仿真”研修班,聽西莫首席技術專家通解電機NVH問題機理,教您如何更好地設計電機!
-
線圈
+關注
關注
14文章
1820瀏覽量
44430 -
電機
+關注
關注
142文章
9001瀏覽量
145340 -
波形
+關注
關注
3文章
379瀏覽量
31544 -
電勢
+關注
關注
0文章
74瀏覽量
13628 -
繞組
+關注
關注
2文章
518瀏覽量
19867
原文標題:電機繞組(七)
文章出處:【微信號:西莫電機論壇,微信公眾號:西莫電機論壇】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
電機繞組的齒諧波電勢
分析三相繞組的合成磁勢
直流測速發(fā)電機及其工作原理(含原理圖)
淺談三相繞組磁勢及其合成磁勢基波
電樞磁場如何產(chǎn)生電樞反應?
電機基礎知識入門之交流繞組、電勢、磁勢等詳細資料免費下載
交流電機繞組的分相





 電機繞組產(chǎn)生的電勢和磁勢
電機繞組產(chǎn)生的電勢和磁勢
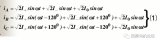










評論