實例詳解貝葉斯推理的原理

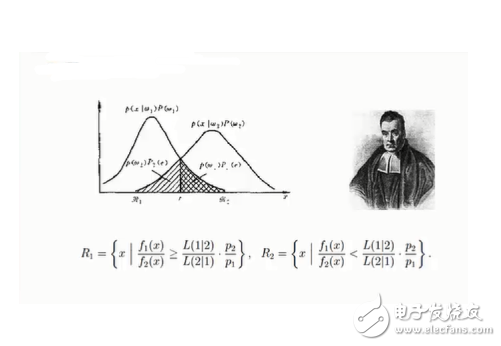
貝葉斯推理是一種精確的數(shù)據(jù)預(yù)測方式。在數(shù)據(jù)沒有期望的那么多，但卻想毫無遺漏地，全面地獲取預(yù)測信息時非常有用。 提及貝葉斯推理時，人們時常會帶著一種敬仰的心情。其實并非想象中那么富有魔力，或是神秘。盡管貝葉斯推理背后的數(shù)學(xué)越來越縝密和復(fù)雜，但其背后概念還是非常容易理解。簡言之，貝葉斯推理有助于大家得到更有力的結(jié)論，將其置于已知的答案中。 貝葉斯推理理念源自托馬斯貝葉斯。三百年前，他是一位從不循規(guī)蹈矩的教會長老院牧師。貝葉斯寫過兩本書，一本關(guān)于神學(xué)，一本關(guān)于概率。他的工作就包括今天著名的貝葉斯定理雛形，自此以后應(yīng)用于推理問題，以及有根據(jù)猜測（educated guessing）術(shù)語中。貝葉斯理念如此流行，得益于一位名叫理查·布萊斯牧師的大力推崇。此人意識到這份定理的重要性后，將其優(yōu)化完善并發(fā)表。因此，此定理變得更加準(zhǔn)確。也因此，歷史上將貝葉斯定理稱之為 Bayes-Price法則。 譯者注：educated guessing 基于(或根據(jù))經(jīng)驗(或?qū)I(yè)知識、手頭資料、事實等)所作的估計(或預(yù)測、猜測、意見等)

影院中的貝葉斯推理

試想一下，你前往影院觀影，前面觀影的小伙伴門票掉了，此時你想引起他們的注意。此圖是他們的背影圖。你無法分辨他們的性別，僅僅知道他們留了長頭發(fā)。那你是說，女士打擾一下，還是說，先生打擾一下。考慮到你對男人和女人發(fā)型的認(rèn)知，或許你會認(rèn)為這位是位女士。（本例很簡單，只存在兩種發(fā)長和性別） 現(xiàn)在將上面的情形稍加變化，此人正在排隊準(zhǔn)備進(jìn)入男士休息室。依靠這個額外的信息，或許你會認(rèn)為這位是位男士。此例采用常識和背景知識即可完成判斷，無需思考。而貝葉斯推理是此方式的數(shù)學(xué)實現(xiàn)形式，得益于此，我們可以做出更加精確的預(yù)測。 我們?yōu)殡娪霸河龅降睦Ь臣由蠑?shù)字。首先假定影院中男女各占一半，100個人中，50個男人，50個女人。女人中，一半為長發(fā)，余下的25人為短發(fā)。而男人中，48位為短發(fā)，兩位為長發(fā)。存在25個長發(fā)女人和2位長發(fā)男人，由此推斷，門票持有者為女士的可能性很大。 100個在男士休息室外排隊，其中98名男士，2位女士為陪同。長發(fā)女人和短發(fā)女人依舊對半分，但此處僅僅各占一種。而男士長發(fā)和短發(fā)的比例依舊保持不變，按照98位男士算，此刻短發(fā)男士有94人，長發(fā)為4人。考慮到有一位長發(fā)女士和四位長發(fā)男士，此刻最有可能的是持票者為男士。這是貝葉斯推理原理的具體案例。事先知曉一個重要的信息線索，門票持有者在男士休息室外排隊，可以幫助我們做出更好的預(yù)測。 為了清晰地闡述貝葉斯推理，需要花些時間清晰地定義我們的理念。不幸的是，這需要用到數(shù)學(xué)知識。除非不得已，我盡量避免此過程太過深奧，緊隨我查看更多的小節(jié)，必定會從中受益。為了大家能夠建立一個基礎(chǔ)，我們需要快速地提及四個概念：概率、條件概率、聯(lián)合概率以及邊際概率。

概率

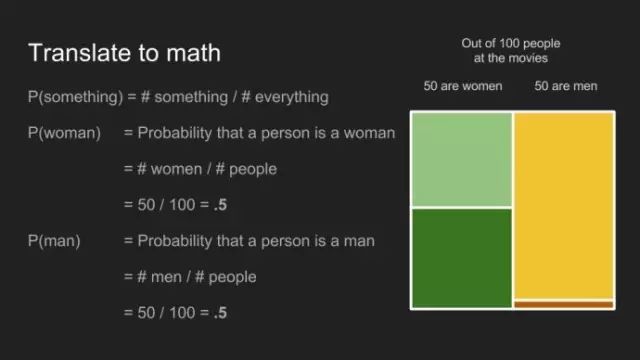
一件事發(fā)生的概率，等于該事件發(fā)生的數(shù)目除以所有事件發(fā)生的數(shù)目。觀影者為一個女士的概率為50位女士除以100位觀影者，即0.5 或50%。換作男士亦如此。

而在男士休息室排列此種情形下，女士概率降至0.02，男士的概率為0.98。 條件概率

條件概率回答了這樣的問題，倘若我知道此人是位女士，其為長發(fā)的概率是多少？條件概率的計算方式和直接得到的概率一樣，但它們更像所有例子中滿足某個特定條件的子集。本例中，此人為女士，擁有長發(fā)的人士的條件概率，P(long hair | woman)為擁有長發(fā)的女士數(shù)目，除以女士的總數(shù)，其結(jié)果為0.5。無論我們是否考慮男士休息室外排隊，或整個影院。

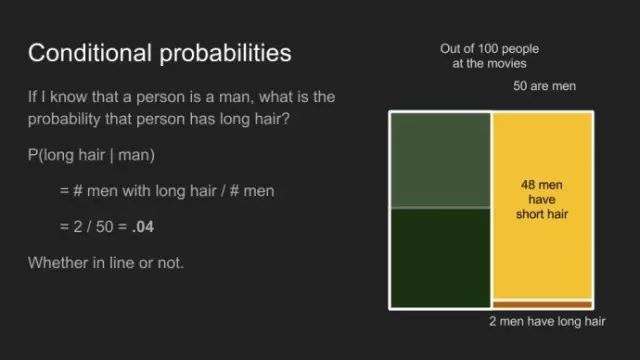
同樣的道理，此人為男士，擁有長發(fā)的條件概率，P(long hair | man)為0.4，不管其是否在隊列中。 很重要的一點，條件概率P(A | B)并不等同于P(B | A)。比如P(cute | puppy)不同于P(puppy | cute)。倘若我抱著的是小狗，可愛的概率是很高的。倘若我抱著一個可愛的東西，成為小狗的概率中等偏下。它有可能是小貓、小兔子、刺猬，甚至一個小人。

聯(lián)合概率

聯(lián)合概率適合回答這樣的問題，此人為一個短發(fā)女人的概率為多少？找出答案需要兩步。首先，我們先看概率是女人的概率，P(woman)。接著，我們給出頭發(fā)短人士的概率，考慮到此人為女士，P(short hair | woman)。通過乘法，進(jìn)行聯(lián)合，給出聯(lián)合概率，P(woman with short hair) = P(woman) * P(short hair | woman)。利用此方法，我們便可計算出我們已知的概率，所有觀影中P(woman with long hair)為0.25，而在男士休息室隊列中的P(woman with long hair)為0.1。不同是因為兩個案例中的P(woman)不同。

相似的，觀影者中P(man with long hair) 為0.02，而在男士休息室隊列中概率為0.04。 和條件概率不同，聯(lián)合概率和順序無關(guān)，P(A and B)等同于P(B and A)。比如，同時擁有牛奶和油炸圈餅的概率，等同于擁有油炸圈餅和牛奶的概率。

邊際概率

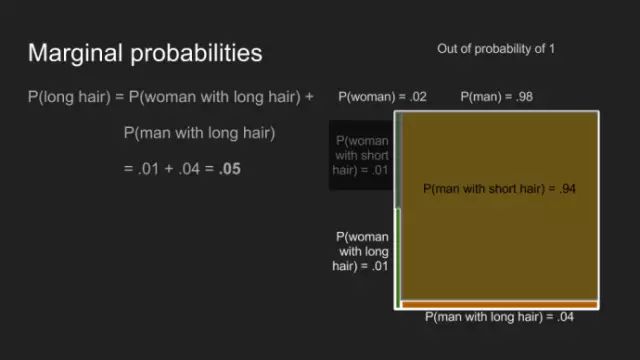
我們最后一個基礎(chǔ)之旅為邊際概率。特別適合回答這樣的問題，擁有長發(fā)人士的概率？為計算出結(jié)果，我們須累加此事發(fā)生的所有概率——即男士留長發(fā)的概率加女士留長發(fā)的概率。加上這兩個概率，即給出所有觀影者P(long hair)的值0.27，而男休息室隊列中的P(long hair)為0.05。

貝葉斯定理

現(xiàn)在到了我們真正關(guān)心的部分。我們想回答這樣的問題，倘若我們知道擁有長發(fā)的人士，那他們是位女士或男士的概率為？這是一個條件概率，P(man | long hair)，為我們已知曉的P(long hair | man)逆方式。因為條件概率不可逆，因此，我們對這個新條件概率知之甚少。 幸運的是托馬斯觀察到一些很酷炫的知識可以幫到我們。

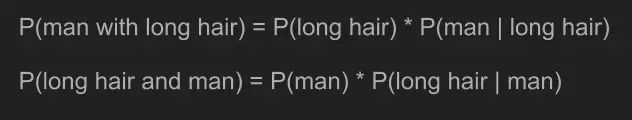
根據(jù)聯(lián)合概率計算規(guī)則，我們給出方程P(man with long hair)和P(long hair and man)。因為聯(lián)合概率可逆，因此這兩個方程等價。

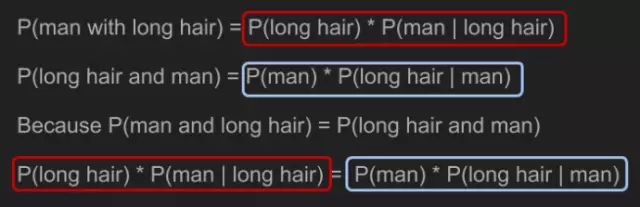
借助一點代數(shù)知識，我們就能解出P(man | long hair)。

表達(dá)式采用A和B，替換“man”和“l(fā)ong hair”，于是我們得到貝葉斯定理。

我們回到最初，借助貝葉斯定理，解決電影院門票困境。

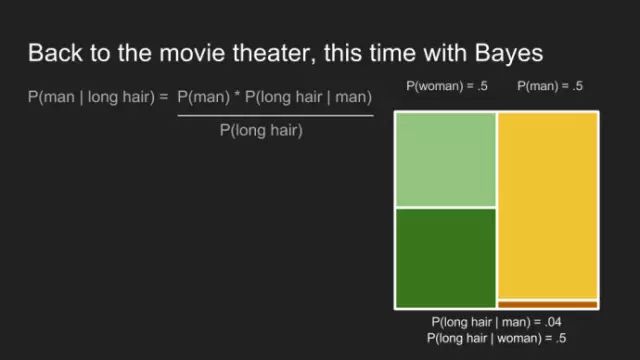
首先，需要計算邊際概率P(long hair)。

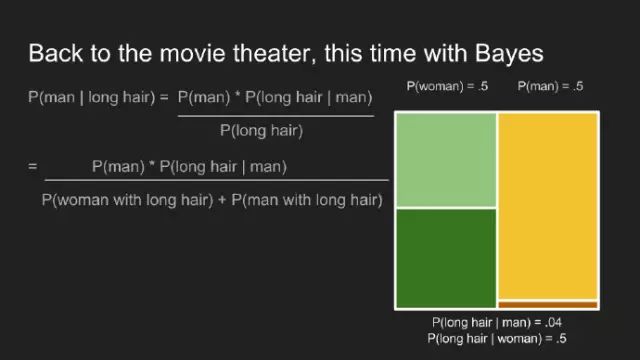
接著代入數(shù)據(jù)，計算出長發(fā)中是男士的概率。對于男士休息室隊列中的觀影者而言，P(man | long hair)微微0.8。這讓我們更加確信一直覺，掉門票的可能是一男士。貝葉斯定理抓住了在此情形下的直覺。更重要的是，更重要的是吸納了先驗知識，男士休息室外隊列中男士遠(yuǎn)多于女士。借用此先驗知識，更新我們對一這情形的認(rèn)識。

概率分布 諸如影院困境這樣的例子，很好地解釋了貝葉斯推理的由來，以及作用機(jī)制。然而，在數(shù)據(jù)科學(xué)應(yīng)用領(lǐng)域，此推理常常用于數(shù)據(jù)解釋。有了我們測出來的先驗知識，借助小數(shù)據(jù)集便可得出更好的結(jié)論。在開始細(xì)說之前，請先允許我先介紹點別的。就是我們需要清楚一個概率分布。 此處可以這樣考慮概率，一壺咖啡正好裝滿一個杯子。倘若用一個杯子來裝沒有問題，那不止一個杯子呢，你需考慮如何將這些咖啡分這些杯子中。當(dāng)然你可以按照自己的意愿，只要將所有咖啡放入某個杯子中。而在電影院，一個杯子或許代表女士或者男士。

或者我們用四個杯子代表性別和發(fā)長的所有組合分布。這兩個案例中，總咖啡數(shù)量累加起來為一杯。

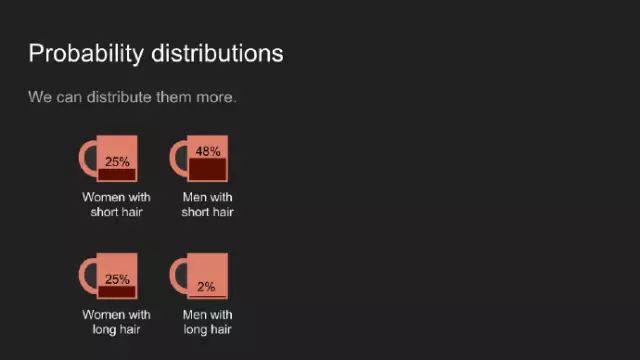
通常，我們將杯子挨個擺放，看其中的咖啡量就像一個柱狀圖。咖啡就像一種信仰，此概率分布用于顯示我們相信某件事情的強(qiáng)烈程度。

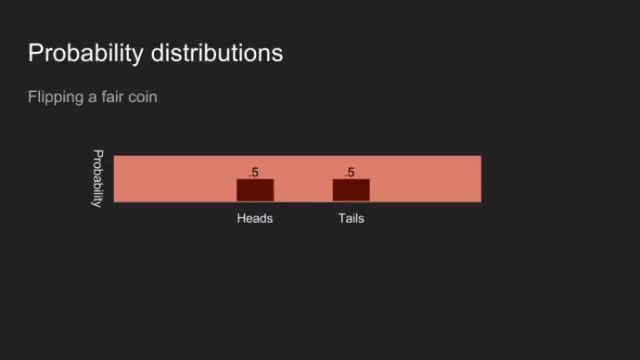
假設(shè)我投了一塊硬幣，然后蓋住它，你會認(rèn)為正面和反面朝上的幾率是一樣的。

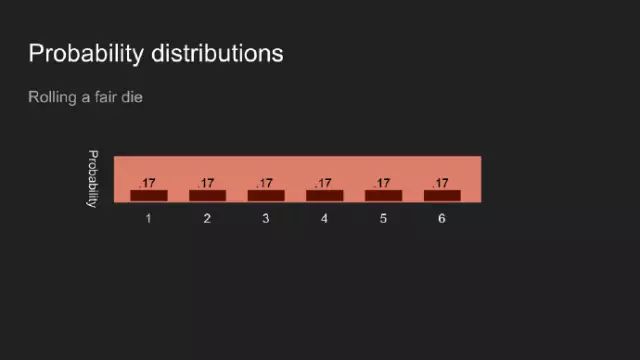
假設(shè)我投了一個骰子，然后蓋住它，你會認(rèn)為六個面中的每一個面朝上的幾率是一樣的。

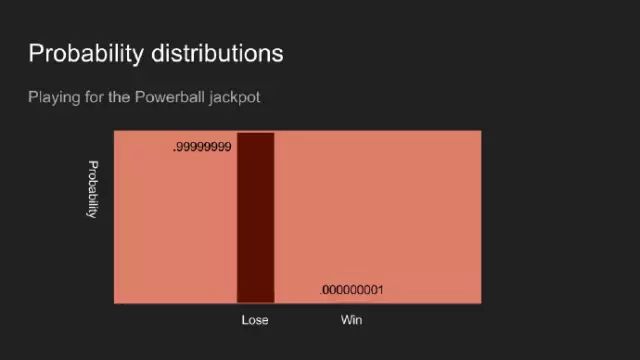
假設(shè)我買了一期強(qiáng)力球彩票，你會認(rèn)為中獎的可能性微乎其微。投硬幣、投骰子、強(qiáng)力球彩票的結(jié)果，都可以視為收集、測量數(shù)據(jù)的例子。

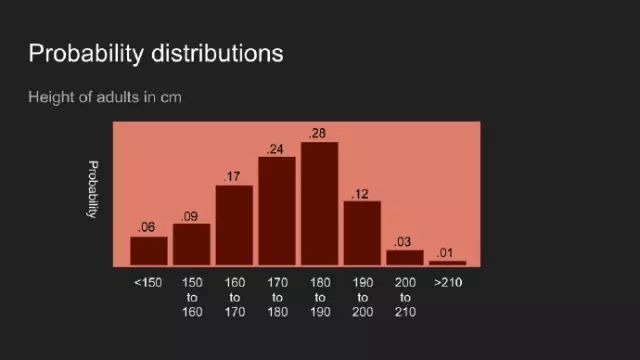
毫無意外，你也可以對其它數(shù)據(jù)持有某種看法。這里我們考慮美國成年人的身高，倘若我告訴你，我見過，并測量了某些人的身高，那你對他們身高的看法，或許如上圖所示。此觀點認(rèn)為一個人的身高可能介于150和200cm之間，最有可能的是介于180和190cm之間。

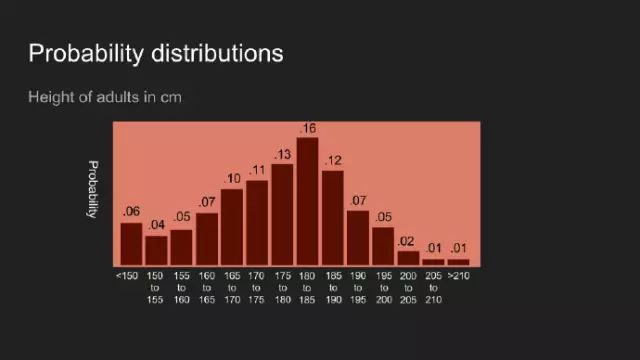
此分布可以分成更多的方格，視作將有限的咖啡放入更多的杯子，以期獲得一組更加細(xì)顆粒度的觀點。

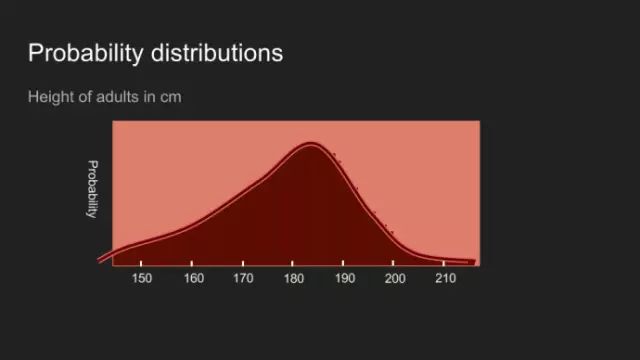
最終虛擬的杯子數(shù)量將非常大，以至于這樣的比喻變得不恰當(dāng)。這樣，分布變得連續(xù)。運用的數(shù)學(xué)方法可能有點變化，但底層的理念還是很有用。此圖表明了你對某一事物認(rèn)知的概率分布。 感謝你們這么有耐心！！有了對概率分布的介紹，我們便可采用貝葉斯定理進(jìn)行數(shù)據(jù)解析了。為了說明這個，我以我家小狗稱重為例。

獸醫(yī)領(lǐng)域的貝葉斯推理

它叫雅各賓當(dāng)政，每次我們?nèi)カF醫(yī)診所，它在秤上總是各種晃動，因此很難讀取一個準(zhǔn)確的數(shù)據(jù)。得到一個準(zhǔn)確的體重數(shù)據(jù)很重要，這是因為，倘若它的體重有所上升，那么我們就得減少其食物的攝入量。它喜歡食物勝過它自己，所以說風(fēng)險蠻大的。 最近一次，在它喪失耐心前，我們測了三次：13.9鎊,17.5鎊以及14.1鎊。這是針對其所做的標(biāo)準(zhǔn)統(tǒng)計分析。計算這一組數(shù)字的均值，標(biāo)準(zhǔn)偏差，標(biāo)準(zhǔn)差，便可得到小狗當(dāng)政的準(zhǔn)確體重分布。

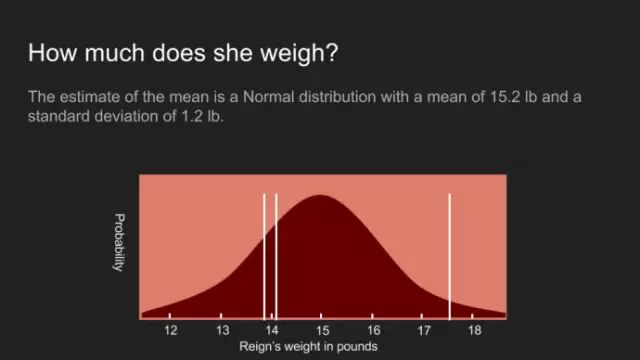
分布展示了我們認(rèn)為的小狗體重，這是一個均值15.2鎊，標(biāo)準(zhǔn)差1.2鎊的正態(tài)分布。真實得測量如白線所示。不幸的是，這個曲線并非理想的寬度。盡管這個峰值為15.2鎊，但概率分布顯示，在13鎊很容易就到達(dá)一個低值，在17鎊到達(dá)一個高值。太過寬泛以致無法做出一個確信的決策。面對如此情形，通常的策略是返回并收集更多的數(shù)據(jù)，但在一些案例中此法操作性不強(qiáng)，或成本高昂。本例中，小狗當(dāng)政的（Reign ）耐心已經(jīng)耗盡，這是我們僅有的測量數(shù)據(jù)。 此時我們需要貝葉斯定理，幫助我們處理小規(guī)模數(shù)據(jù)集。在使用定理前，我們有必要重新回顧一下這個方程，查看每個術(shù)語。

我們用“w” (weight)和 “m” (measurements)替換“A” and “B” ，以便更清晰地表示我們?nèi)绾斡么硕ɡ怼Ｋ膫€術(shù)語分別代表此過程的不同部分。 先驗概率，P(w)，表示已有的事物認(rèn)知。本例中，表示未稱量時，我們認(rèn)為的當(dāng)政體重w。 似然值，P(m | w)，表示針對某個具體體重w所測的值m。又叫似然數(shù)據(jù)。 后驗概率，P(w | m)，表示稱量后，當(dāng)政為某個體重w的概率。當(dāng)然這是我們最感興趣的。 譯者注：后驗概率，通常情況下，等于似然值乘以先驗值。是我們對于世界的內(nèi)在認(rèn)知。 概率數(shù)據(jù)，P(m)，表示某個數(shù)據(jù)點被測到的概率。本例中，我們假定它為一個常量，且測量本身沒有偏向。 對于完美的不可知論者來說，也不是什么特別糟糕的事情，而且無需對結(jié)果做出什么假設(shè)。例如本例中，即便假定當(dāng)Reign的體重為13鎊、或1鎊，或1000000 鎊，讓數(shù)據(jù)說話。我們先假定一個均一的先驗概率，即對所有值而言，概率分布就一常量值。貝葉斯定理便可簡化為P(w | m) = P(m | w)。

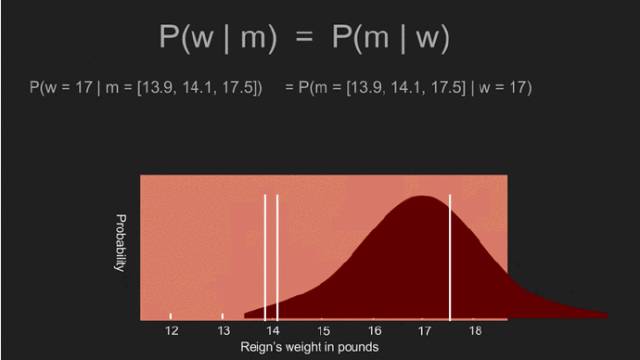
此刻，借助Reign的每個可能體重，我們計算出三個測量的似然值。比如，倘若當(dāng)政的體重為1000鎊，極端的測量值是不太可能的。然而，倘若當(dāng)政的體重為14鎊或16鎊。我們可以遍歷所有，利用Reign的每一個假設(shè)體重值，計算出測量的似然值。這便是P(m | w)。得益于這個均一的先驗概率，它等同于后驗概率分布 P(w | m)。 這并非偶然。通過均值、標(biāo)準(zhǔn)偏差、標(biāo)準(zhǔn)差得來的，很像答案。實際上，它們是一樣的，采用一個均一的先驗概率給出傳統(tǒng)的統(tǒng)計估測結(jié)果。峰值所在的曲線位置，均值，15.2鎊也叫體重的極大似然估計（MLE）。 即使采用了貝葉斯定理，但依舊離有用的估計很遠(yuǎn)。為此，我們需要非均一先驗概率。先驗分布表示未測量情形下對某事物的認(rèn)知。均一的先驗概率認(rèn)為每個可能的結(jié)果都是均等的，通常都很罕見。在測量時，對某些量已有些認(rèn)識。年齡總是大于零，溫度總是大于-276攝氏度。成年人身高罕有超過8英尺的。某些時候，我們擁有額外的領(lǐng)域知識，一些值很有可能出現(xiàn)在其它值中。

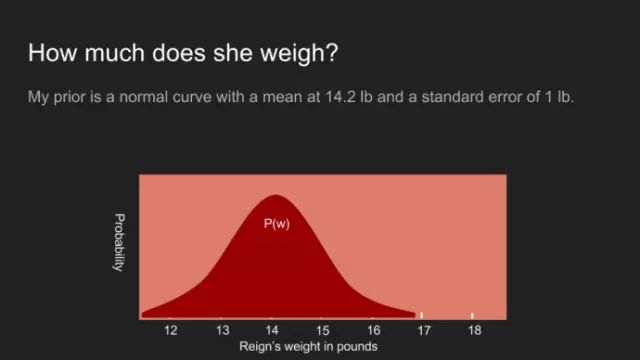
在Reign的案例中，我確實擁有其它的信息。我知道上次它在獸醫(yī)診所稱到的體重是14.2鎊。我還知道它并不是特別顯胖或顯瘦，即便我的胳膊對重量不是特別敏感。有鑒于此，它大概重14.2鎊，相差一兩鎊上下。為此，我選用峰值為14.2鎊。標(biāo)準(zhǔn)偏差為0.5鎊的正態(tài)分布。

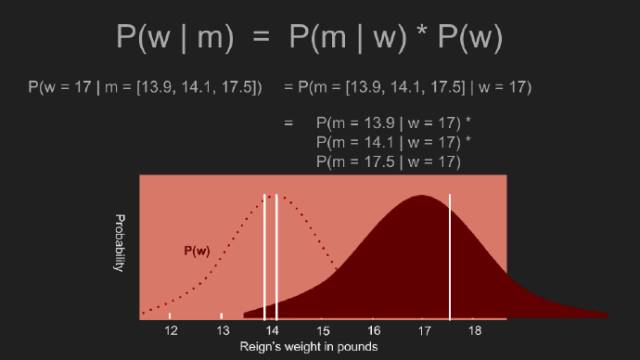
先驗概率已經(jīng)就緒，我們重復(fù)計算后驗概率。為此，我們考慮某一概率，此時Reign體重為某一特定值，比如17鎊。接著，17鎊這一似然值乘以測量值為17這一條件概率。接著，對于其它可能的體重，我們重復(fù)這一過程。先驗概率的作用是降低某些概率，擴(kuò)大另一些概率。本例中，在區(qū)間13-15鎊增加更多的測量值，以外的區(qū)間則減少更多的測量值。這與均一先驗概率不同，給出一個恰當(dāng)?shù)母怕剩?dāng)政的真實體重為17鎊。借助非均勻的先驗概率，17鎊掉入分布式的尾部。乘以此概率值使得體重為17鎊的似然值變低。

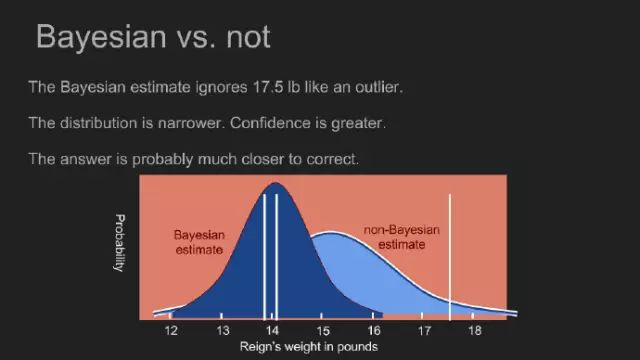
通過計算當(dāng)政每一個可能的體重概率，我們得到一個新的后驗概率。后驗概率分布的峰值也叫最大后驗概率（MAP），本例為14.1鎊。這和均一先驗概率有明顯的不同。此峰值更窄，有助于我們做出一個更可信的估測。現(xiàn)在來看，小狗當(dāng)政的體重變化不大，它的體型依舊如前。 通過吸收已有的測量認(rèn)知，我們可以做出一個更加準(zhǔn)確的估測，其可信度高于其他方法。這有助于我們更好地使用小量數(shù)據(jù)集。先驗概率賦予17.5鎊的測量值是一個比較低的概率。這幾乎等同于反對此偏離正常值的測量值。不同于直覺和常識的異常檢測方式，貝葉斯定理有助于我們采用數(shù)學(xué)的方式進(jìn)行異常檢測。 另外，假定術(shù)語P(m)是均一的，但恰巧我們知道稱量存在某種程度的偏好，這將反映在P(m)中。若稱量僅輸出某些數(shù)字，或返回讀數(shù)2.0，占整個時間的百分之10，或第三次嘗試產(chǎn)生一個隨機(jī)測量值，均需要手動修改P(m)以反映這一現(xiàn)象，以便后驗概率更加準(zhǔn)確。 規(guī)避貝葉斯陷阱 探究Reign的真實體重體現(xiàn)了貝葉斯的優(yōu)勢。但這也存在某些陷阱。通過一些假設(shè)我們改進(jìn)了估測，而測量某些事物的目的就是為了了解它。倘若我們假定對某一答案有所了解，我們可能會刪改此數(shù)據(jù)。馬克·吐溫對強(qiáng)先驗的危害做了簡明地闡述，“將你陷入困境的不是你所不知道的，而是你知道的那些看似正確的東西。” 假如采取強(qiáng)先驗假設(shè)，當(dāng)Reign的體重在13與15鎊之間，再假如其真實體重為12.5鎊，我們將無法探測到。先驗認(rèn)知認(rèn)為此結(jié)果的概率為零，不論做多少次測量，低于13鎊的測量值都認(rèn)為無效。 幸運的是，有一種兩面下注的辦法，可以規(guī)避這種盲目地刪除。針對對于每一個結(jié)果至少賦予一個小的概率，倘若借助物理領(lǐng)域的一些奇思妙想，當(dāng)政確實能稱到1000鎊，那我們收集的測量值也能反映在后驗概率中。這也是正態(tài)分布作為先驗概率的原因之一。此分布集中了我們對一小撮結(jié)果的大多數(shù)認(rèn)識，不管怎么延展，其尾部再長都不會為零。 在此，紅桃皇后是一個很好的榜樣： 愛麗絲笑道：“試了也沒用，沒人會相信那些不存在的事情。”

“我敢說你沒有太多的練習(xí)”，女王回應(yīng)道，“我年輕的時候，一天中的一個半小時都在閉上眼睛，深呼吸。為何，那是因為有時在早飯前，我已經(jīng)意識到存在六種不可能了。”來自劉易斯·卡羅爾的《愛麗絲漫游奇境》

編輯：黃飛