算法技巧就那幾個套路,如果你心里有數,就會輕松很多,本文就來扒一扒動態規劃的褲子,形成一套解決這類問題的思維框架。廢話不多說了,上干貨。
動態規劃問題的一般形式就是求最值 。動態規劃其實是運籌學的一種最優化方法,只不過在計算機問題上應用比較多,比如說讓你求最長遞增子序列呀,最小編輯距離呀等等。
既然是要求最值,核心問題是什么呢? 求解動態規劃的核心問題是窮舉 。因為要求最值,肯定要把所有可行的答案窮舉出來,然后在其中找最值唄。
動態規劃就這么簡單,就是窮舉就完事了?我看到的動態規劃問題都很難啊!
首先,動態規劃的窮舉有點特別,因為這類問題 存在「重疊子問題」 ,如果暴力窮舉的話效率會極其低下,所以需要「備忘錄」或者「DP table」來優化窮舉過程,避免不必要的計算。
而且,動態規劃問題一定會 具備「最優子結構」 ,才能通過子問題的最值得到原問題的最值。
另外,雖然動態規劃的核心思想就是窮舉求最值,但是問題可以千變萬化,窮舉所有可行解其實并不是一件容易的事,只有列出 正確的「狀態轉移方程 」 才能正確地窮舉。
以上提到的重疊子問題、最優子結構、狀態轉移方程就是動態規劃三要素。具體什么意思等會會舉例詳解,但是在實際的算法問題中, 寫出狀態轉移方程是最困難的 ,這也就是為什么很多朋友覺得動態規劃問題困難的原因,我來提供我研究出來的一個思維框架,輔助你思考狀態轉移方程:
明確「狀態」 -> 定義 dp 數組/函數的含義 -> 明確「選擇」-> 明確 base case。
下面通過斐波那契數列問題和湊零錢問題來詳解動態規劃的基本原理。前者主要是讓你明白什么是重疊子問題(斐波那契數列嚴格來說不是動態規劃問題),后者主要集中于如何列出狀態轉移方程。
請讀者不要嫌棄這個例子簡單, 只有簡單的例子才能讓你把精力充分集中在算法背后的通用思想和技巧上,而不會被那些隱晦的細節問題搞的莫名其妙 。想要困難的例子,歷史文章里有的是。
一、斐波那契數列
1、暴力遞歸
斐波那契數列的數學形式就是遞歸的,寫成代碼就是這樣:
int fib(int N) {
if (N == 1 || N == 2) return 1;
return fib(N - 1) + fib(N - 2);
}
這個不用多說了,學校老師講遞歸的時候似乎都是拿這個舉例。我們也知道這樣寫代碼雖然簡潔易懂,但是十分低效,低效在哪里?假設 n = 20,請畫出遞歸樹。
PS:但凡遇到需要遞歸的問題,最好都畫出遞歸樹,這對你分析算法的復雜度,尋找算法低效的原因都有巨大幫助。
這個遞歸樹怎么理解?就是說想要計算原問題f(20),我就得先計算出子問題f(19)和f(18),然后要計算f(19),我就要先算出子問題f(18)和f(17),以此類推。最后遇到f(1)或者f(2)的時候,結果已知,就能直接返回結果,遞歸樹不再向下生長了。
遞歸算法的時間復雜度怎么計算?子問題個數乘以解決一個子問題需要的時間。
子問題個數,即遞歸樹中節點的總數。顯然二叉樹節點總數為指數級別,所以子問題個數為 O(2^n)。
解決一個子問題的時間,在本算法中,沒有循環,只有 f(n - 1) + f(n - 2) 一個加法操作,時間為 O(1)。
所以,這個算法的時間復雜度為 O(2^n),指數級別,爆炸。
觀察遞歸樹,很明顯發現了算法低效的原因:存在大量重復計算,比如f(18)被計算了兩次,而且你可以看到,以f(18)為根的這個遞歸樹體量巨大,多算一遍,會耗費巨大的時間。更何況,還不止f(18)這一個節點被重復計算,所以這個算法及其低效。
這就是動態規劃問題的第一個性質: 重疊子問題 。下面,我們想辦法解決這個問題。
2、帶備忘錄的遞歸解法
明確了問題,其實就已經把問題解決了一半。即然耗時的原因是重復計算,那么我們可以造一個「備忘錄」,每次算出某個子問題的答案后別急著返回,先記到「備忘錄」里再返回;每次遇到一個子問題先去「備忘錄」里查一查,如果發現之前已經解決過這個問題了,直接把答案拿出來用,不要再耗時去計算了。
一般使用一個數組充當這個「備忘錄」,當然你也可以使用哈希表(字典),思想都是一樣的。
int fib(int N) {
if (N < 1) return 0;
// 備忘錄全初始化為 0
vector<int> memo(N + 1, 0);
// 初始化最簡情況
return helper(memo, N);
}
int helper(vector<int>& memo, int n) {
// base case
if (n == 1 || n == 2) return 1;
// 已經計算過
if (memo[n] != 0) return memo[n];
memo[n] = helper(memo, n - 1) +
helper(memo, n - 2);
return memo[n];
}
現在,畫出遞歸樹,你就知道「備忘錄」到底做了什么:
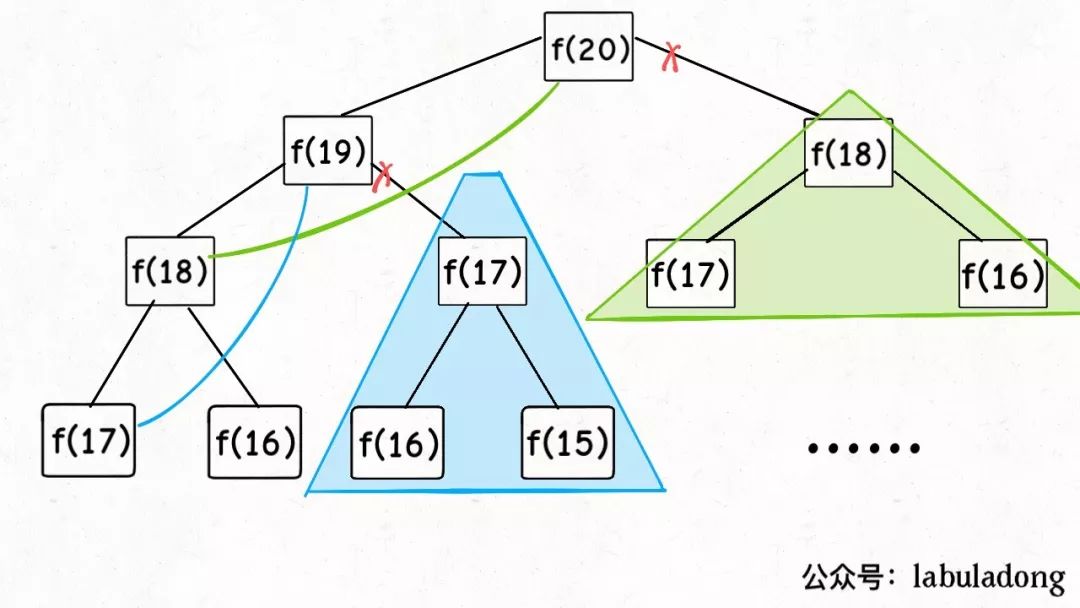
實際上,帶「備忘錄」的遞歸算法,把一棵存在巨量冗余的遞歸樹通過「剪枝」,改造成了一幅不存在冗余的遞歸圖,極大減少了子問題(即遞歸圖中節點)的個數。
遞歸算法的時間復雜度怎么算? 子問題個數乘以解決一個子問題需要的時間。
子問題個數,即圖中節點的總數,由于本算法不存在冗余計算,子問題就是f(1),f(2),f(3)…f(20),數量和輸入規模 n = 20 成正比,所以子問題個數為 O(n)。
解決一個子問題的時間,同上,沒有什么循環,時間為 O(1)。
所以,本算法的時間復雜度是 O(n)。比起暴力算法,是降維打擊。
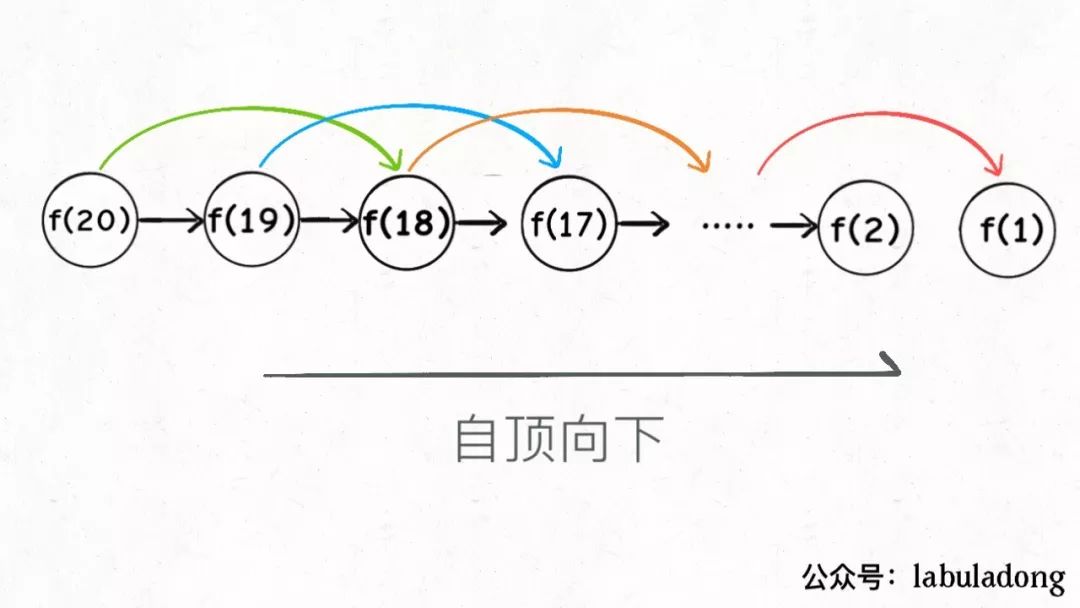
至此,帶備忘錄的遞歸解法的效率已經和迭代的動態規劃一樣了。實際上,這種解法和迭代的動態規劃思想已經差不多,只不過這種方法叫做「自頂向下」,動態規劃叫做「自底向上」。
啥叫「自頂向下」? 注意我們剛才畫的遞歸樹(或者說圖),是從上向下延伸,都是從一個規模較大的原問題比如說f(20),向下逐漸分解規模,直到f(1)和f(2)觸底,然后逐層返回答案,這就叫「自頂向下」。
啥叫「自底向上」? 反過來,我們直接從最底下,最簡單,問題規模最小的f(1)和f(2)開始往上推,直到推到我們想要的答案f(20),這就是動態規劃的思路,這也是為什么動態規劃一般都脫離了遞歸,而是由循環迭代完成計算。
3、dp 數組的迭代解法
有了上一步「備忘錄」的啟發,我們可以把這個「備忘錄」獨立出來成為一張表,就叫做 DP table 吧,在這張表上完成「自底向上」的推算豈不美哉!
int fib(int N) {
vector<int> dp(N + 1, 0);
// base case
dp[1] = dp[2] = 1;
for (int i = 3; i <= N; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[N];
}
畫個圖就很好理解了,而且你發現這個 DP table 特別像之前那個「剪枝」后的結果,只是反過來算而已。實際上,帶備忘錄的遞歸解法中的「備忘錄」,最終完成后就是這個 DP table,所以說這兩種解法其實是差不多的,大部分情況下,效率也基本相同。
這里,引出「狀態轉移方程」這個名詞,實際上就是描述問題結構的數學形式:
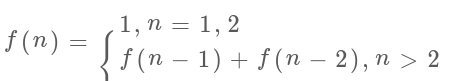
為啥叫「狀態轉移方程」?為了聽起來高端。你把 f(n) 想做一個狀態 n,這個狀態 n 是由狀態 n - 1 和狀態 n - 2 相加轉移而來,這就叫狀態轉移,僅此而已。
你會發現,上面的幾種解法中的所有操作,例如 return f(n - 1) + f(n - 2),dp[i] = dp[i - 1] + dp[i - 2],以及對備忘錄或 DP table 的初始化操作,都是圍繞這個方程式的不同表現形式。可見列出「狀態轉移方程」的重要性,它是解決問題的核心。很容易發現,其實狀態轉移方程直接代表著暴力解法。
千萬不要看不起暴力解,動態規劃問題最困難的就是寫出狀態轉移方程 ,即這個暴力解。優化方法無非是用備忘錄或者 DP table,再無奧妙可言。
這個例子的最后,講一個細節優化。細心的讀者會發現,根據斐波那契數列的狀態轉移方程,當前狀態只和之前的兩個狀態有關,其實并不需要那么長的一個 DP table 來存儲所有的狀態,只要想辦法存儲之前的兩個狀態就行了。所以,可以進一步優化,把空間復雜度降為 O(1):
int fib(int n) {
if (n == 2 || n == 1)
return 1;
int prev = 1, curr = 1;
for (int i = 3; i <= n; i++) {
int sum = prev + curr;
prev = curr;
curr = sum;
}
return curr;
}
有人會問,動態規劃的另一個重要特性「最優子結構」,怎么沒有涉及?下面會涉及。斐波那契數列的例子嚴格來說不算動態規劃,因為沒有涉及求最值,以上旨在演示算法設計螺旋上升的過程。
下面,看第二個例子,湊零錢問題。
-
計算機
+關注
關注
19文章
7518瀏覽量
88192 -
函數
+關注
關注
3文章
4338瀏覽量
62739 -
動態規劃
+關注
關注
0文章
17瀏覽量
8930
發布評論請先 登錄
相關推薦
企業節能規劃指南
TSC動態補償柜選型指南
基于動態規劃法的電力資源的合理分配
基于時延Q學習的機器人動態規劃方法

分層學習的自適應動態規劃
動態規劃方法的利用matlab實現及其應用的有效工具詳細資料概述




 動態規劃詳細指南(上)
動態規劃詳細指南(上)
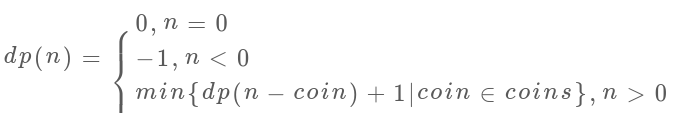










評論