使用溫度計(jì)算和阿倫尼烏斯方程了解電阻和放大器的老化行為,以了解電阻漂移、電阻穩(wěn)定性和運(yùn)算放大器漂移。
之前,我們討論了高溫加速老化方法,該方法使用相對(duì)較短的測(cè)試持續(xù)時(shí)間來評(píng)估電子元件的長期穩(wěn)定性。
在本文中,我們將繼續(xù)討論,并了解電阻和放大器的老化行為。
老化預(yù)測(cè)—老化引起的電阻漂移
首先,讓我們記住電阻的值會(huì)隨著時(shí)間的推移而變化。在許多電路中,只需要大致的精度,電阻老化可能不是一個(gè)嚴(yán)重的問題。然而,某些精密應(yīng)用要求電阻器在規(guī)定的使用壽命內(nèi)長期漂移低至百萬分之幾。因此,開發(fā)具有足夠精度的老化預(yù)測(cè)模型非常重要,以確保所采用的精密電阻在系統(tǒng)的整個(gè)生命周期內(nèi)保持指定的精度。一家名為Vishay的公司建議使用以下公式(公式1)來計(jì)算薄膜電阻器的長期變化:


是電阻器在溫度下所需工作時(shí)間t之后的漂移值θj。
公式1顯示,將電阻的工作溫度提高30°K,其長期漂移會(huì)增加2倍。此外,漂移隨著操作時(shí)間的立方根而增加。例如,如果電阻在1000°C時(shí)的125小時(shí)漂移小于0.25%,則電阻在相同溫度下工作8000小時(shí)后漂移(θj=θ0)估算公式為:

用于電阻老化預(yù)測(cè)的阿倫尼烏斯方程
在公式1中,考慮溫度依賴性的項(xiàng)來自阿倫尼烏斯速率定律,該定律在下面也重復(fù)為公式2:

等式 2.
該方程指定了反應(yīng)速度如何隨開爾文 (T)溫度變化。根據(jù)Vishay的說法,薄膜和箔電阻器的老化過程都遵循阿倫尼烏斯方程。圖1顯示了相同箔電阻在不同溫度下的老化數(shù)據(jù)。

* 圖1. 圖片由 Vishay 提供*
在此圖中,電阻漂移分布標(biāo)準(zhǔn)差的自然對(duì)數(shù)(Ln(D 標(biāo)清 )) 被策劃反對(duì)1000/T.
請(qǐng)注意,直線可以適合這些數(shù)據(jù)點(diǎn)。這與阿倫尼烏斯方程一致,阿倫尼烏斯方程可以表示為:
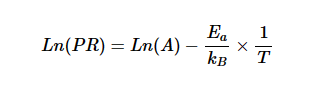
該方程表明 Ln(PR) 與1/T1是反應(yīng)服從阿倫尼烏斯方程時(shí)的直線。
由于這種關(guān)系適用于圖1中的數(shù)據(jù)點(diǎn),因此我們可以得出結(jié)論,這些電阻的老化過程遵循阿倫尼烏斯定律。
估算電阻溫度—提高電阻器的長期穩(wěn)定性
根據(jù)公式1,將電阻保持在較低溫度可以減少其隨時(shí)間推移的漂移。剩下的問題是,我們?nèi)绾尾拍鼙3蛛娮杵鞯臏囟雀停?/p>
公式1中的θ項(xiàng)是指電阻溫度,而不是環(huán)境溫度。電阻溫度(θ 電阻器 ) 可以通過以下公式估算:
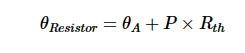
θ一個(gè)是環(huán)境溫度
R千是電阻器的熱阻
P為電阻中的功耗
該公式表明,除了環(huán)境溫度外,電阻中的散熱和熱阻值也會(huì)影響電阻溫度。為了使電阻器運(yùn)行得更低,我們可以盡可能限制電阻器中的功耗。此外,改變印刷電路板的特性,如走線密度和電源/接地層的數(shù)量,可以改變系統(tǒng)的有效熱阻值。這種變化是因?yàn)橛∷㈦娐钒宄洚?dāng)焊接在電阻上的散熱器。更高效的散熱器可以改善傳熱并保持電路組件(包括精密電阻器)更冷。
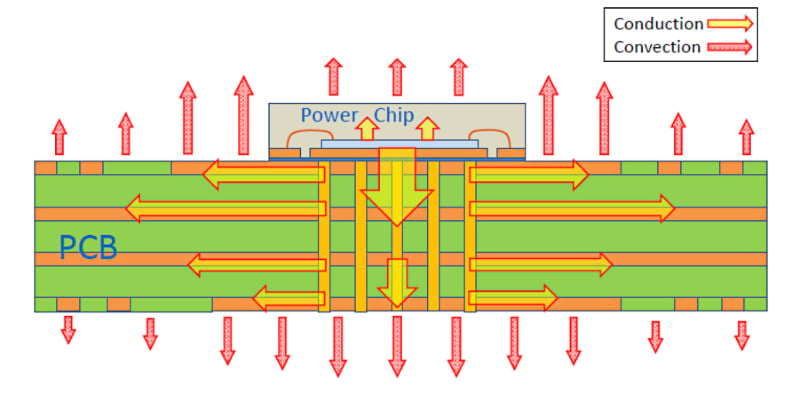
***圖2. *圖片由安森美美提供
通過調(diào)整不同的設(shè)計(jì)參數(shù),我們可以嘗試將電阻溫度保持在 85 °C 的典型最大值以下,以提高長期穩(wěn)定性。
還值得一提的是,在高于標(biāo)稱值的功率水平下工作電阻會(huì)導(dǎo)致長期漂移大于基于阿倫尼烏斯的方程預(yù)測(cè)的漂移。在額定功率以上,電阻材料中加速老化過程的部分可能會(huì)出現(xiàn)一些熱點(diǎn)。這可能導(dǎo)致漂移值大于電阻平均溫度預(yù)測(cè)的值。
運(yùn)算放大器老化效應(yīng)和長期運(yùn)算放大器漂移
放大器的輸入失調(diào)電壓也會(huì)因老化而變化。這會(huì)產(chǎn)生隨時(shí)間變化的誤差,并限制可測(cè)量的最小直流信號(hào)。雖然典型通用精密運(yùn)算放大器的失調(diào)隨溫度的漂移在1–10 μV/°C范圍內(nèi),但在工作的前30天內(nèi),老化引起的運(yùn)算放大器失調(diào)變化約為幾μV。
我們討論了電阻器的長期漂移隨著其工作時(shí)間的立方根而增加,晶體老化往往與時(shí)間呈對(duì)數(shù)關(guān)系。由于老化而導(dǎo)致的運(yùn)算放大器失調(diào)電壓偏差也是時(shí)間的非線性函數(shù)。運(yùn)算放大器失調(diào)的長期漂移與經(jīng)過時(shí)間的平方根成正比。因此,如果將老化效應(yīng)指定為1 μV/1000小時(shí),則失調(diào)可以變化約3 μV/年,計(jì)算如下:
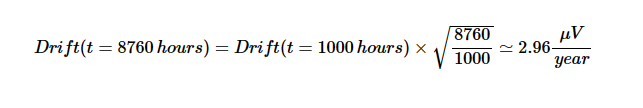
失調(diào)的長期變化通常以μV/月或μV/1000小時(shí)為單位。
隨機(jī)游走現(xiàn)象:電子元件老化是一個(gè)隨機(jī)過程
需要注意的是,老化效應(yīng)是一個(gè)隨機(jī)過程,設(shè)備的實(shí)際老化行為可能過于復(fù)雜,無法用簡(jiǎn)單的公式來描述。衰老有時(shí)被認(rèn)為是一種“隨機(jī)游走”現(xiàn)象。當(dāng)集成不相關(guān)的隨機(jī)“步驟”時(shí),會(huì)產(chǎn)生隨機(jī)游走過程。其離散時(shí)間表示由下式給出:
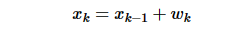
- x
k和 xK-1是隨機(jī)過程的兩個(gè)連續(xù)樣本(我們討論中的老化效應(yīng)) - w
k是白噪聲
下面的圖3顯示了白噪聲的示例以及從相同的白噪聲中獲得的隨機(jī)游走。
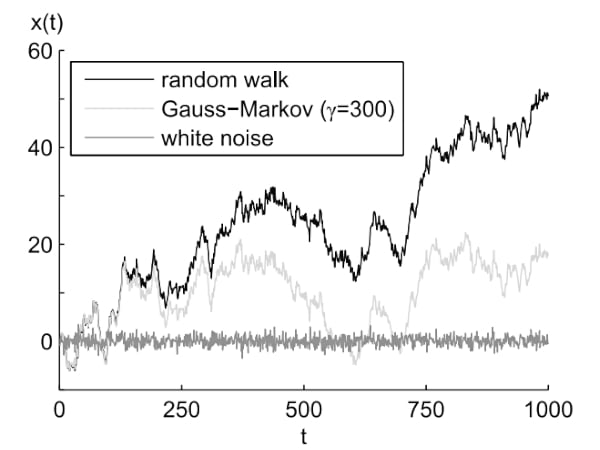
* 圖3. 圖片由《信號(hào)處理系統(tǒng)手冊(cè)》提供*
在隨機(jī)游走過程中,我們積分的步驟越多,我們就越有可能偏離初始值。在從電子元件收集的老化數(shù)據(jù)中也觀察到了類似的趨勢(shì)。例如,將圖3中的上述隨機(jī)游走過程與下面圖1461所示的LT30在4 °C下測(cè)得的長期漂移進(jìn)行比較。

* 圖4. LT1461 的長期漂移圖。圖片由凌力爾特提供*
如果使用零均值白噪聲生成隨機(jī)游走過程,則隨機(jī)游走過程的兩個(gè)任意樣本[視頻]之間的平均差將與兩個(gè)樣本之間時(shí)間差的平方根成正比。這與我們上面討論的用于模擬運(yùn)算放大器失調(diào)電壓的長期漂移的簡(jiǎn)單方程一致,其中假設(shè)漂移與經(jīng)過時(shí)間的平方根成正比。
隨機(jī)游走可能是重要的過程,并出現(xiàn)在其他各種科學(xué)和社會(huì)學(xué)科中。例如,隨機(jī)游走過程可以對(duì)MEMS陀螺儀輸出端出現(xiàn)的部分噪聲進(jìn)行建模。在本系列的下一篇文章中,我們將研究基準(zhǔn)電壓源的老化行為。
-
電阻器
+關(guān)注
關(guān)注
21文章
3779瀏覽量
62114 -
運(yùn)算放大器
+關(guān)注
關(guān)注
215文章
4929瀏覽量
172848 -
電子元件
+關(guān)注
關(guān)注
94文章
1355瀏覽量
56507
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
運(yùn)算放大器的主要應(yīng)用與硬性要求
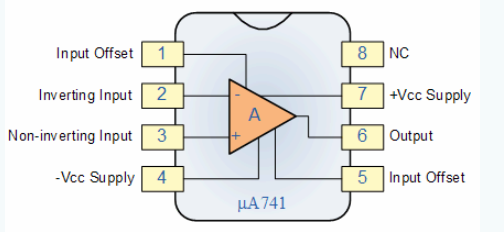
淺談運(yùn)算放大器和比較器
運(yùn)算放大器微分電路解析
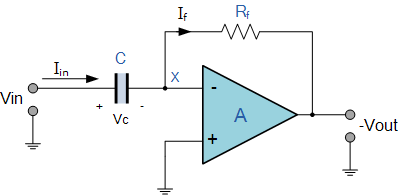
什么是運(yùn)算放大器和比較器?
什么是運(yùn)算放大器和比較器?
通用運(yùn)算放大器(Op-Amp)應(yīng)用及分析
1%電阻器和運(yùn)算放大器可以構(gòu)建一個(gè)完全合格的差動(dòng)放大器嗎?
你會(huì)為了運(yùn)算放大器電路的輸入DC電阻而添加一個(gè)電阻器嗎?
電子元件包括哪些
運(yùn)算放大器設(shè)計(jì)演示板
運(yùn)算放大器,運(yùn)算放大器是什么意思
面向運(yùn)算放大器應(yīng)用的電阻器網(wǎng)絡(luò)
51單片機(jī)學(xué)習(xí)筆記一,電子元件(運(yùn)算放大器)





 電子元件老化——電阻器和運(yùn)算放大器的老化效應(yīng)
電子元件老化——電阻器和運(yùn)算放大器的老化效應(yīng)










評(píng)論