1 信號與系統的基本概念
信號是信息和消息傳播的載體和工具,一般表現為隨時間不斷變化的某種物理量或者物理參數。
信號:基帶信號、載波信號、已調信號、噪聲,……
系統是指由若干相互有聯系的事物組合而成的整體,用于將送入系統的輸入信號進行加工處理、運算變換后得到期望的輸出信號,或者將信號傳輸到接收端。
系統:通信系統、發射機、接收機、信道、……
信號的分類:
連續信號、離散信號、數字信號
確定信號、隨機信號——
確定信號:能夠用確定的時間函數表達式或波形圖描述,在任一指定時刻的幅度都可以根據函數表達式或波形圖來確定。
隨機信號:如果沒有確定的時間函數表達式,在任一時刻的幅度取值事先都不可確定,而只知道幅度取為某個數值的概率有多大。
2 傅里葉變換與信號的頻譜
2.1 信號的頻譜
頻譜(Spectrum)
通過傅里葉變換可以將信號分解為不同頻率的正弦信號分量的疊加,而信號的傅里葉變換F(jω)反映了信號中各分量的幅度和相位隨其角頻率ω的變化關系。
稱為信號的頻譜密度。 簡稱為頻譜(Spectrum)。
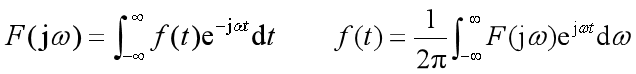
幅度譜、相位譜
對實信號,幅度譜為偶函數,相位譜為奇函數
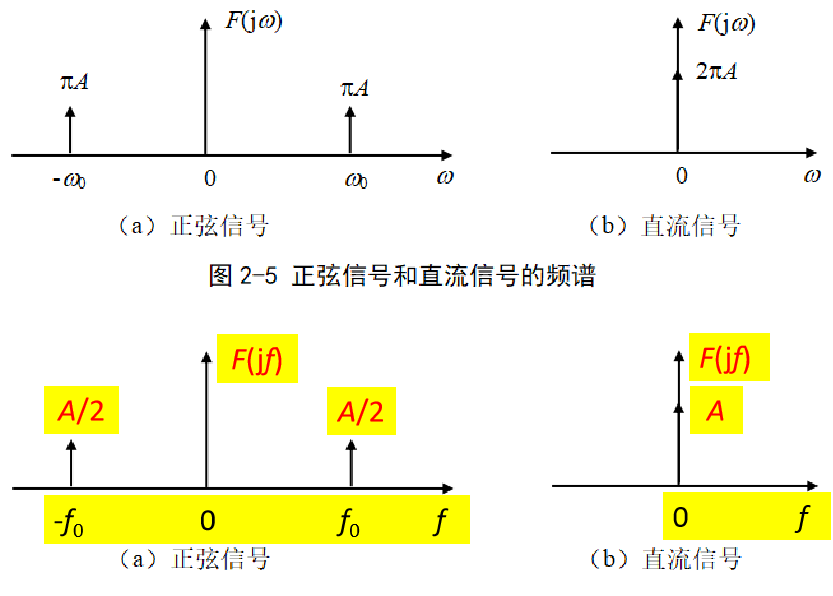
單邊譜、雙邊譜
能量信號的頻譜
所有能量信號的頻譜都不含有沖激函數,而是以ω為自變量的連續或者分段函數。
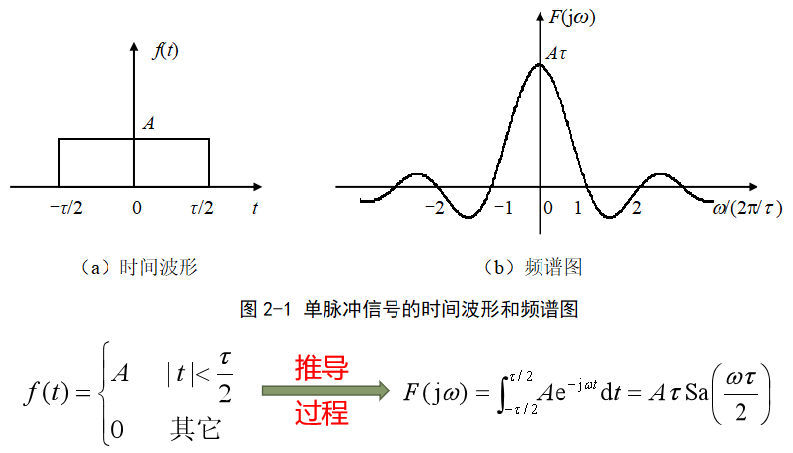
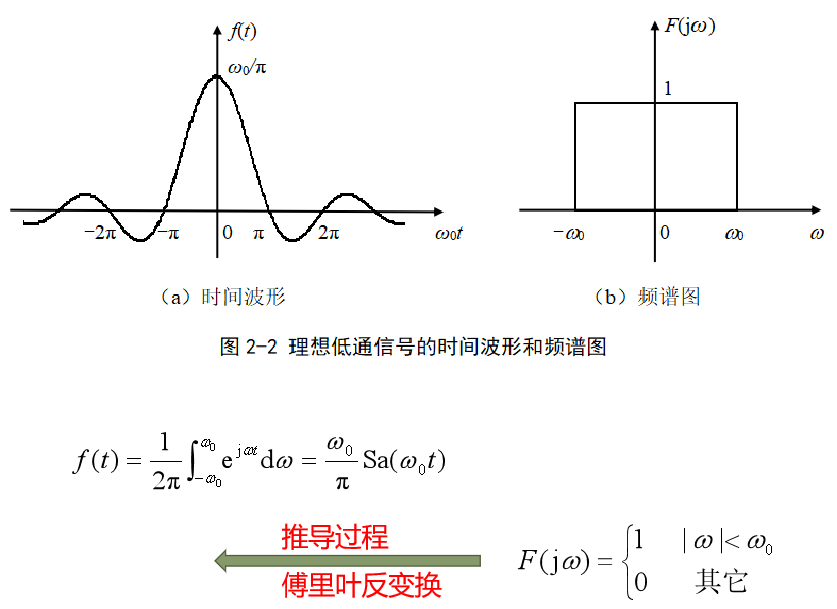
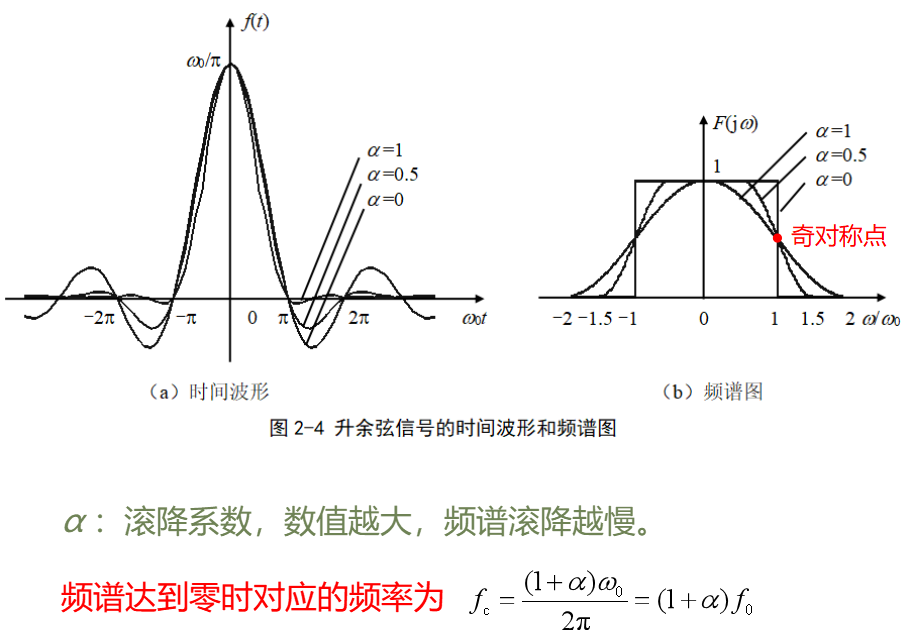
周期信號的頻譜
周期信號的頻譜由無窮多個沖激構成,各沖激函數位于基波角頻率的整數倍位置。
因此周期信號的頻譜都是離散譜,而非周期信號和能量信號的頻譜都是連續譜。
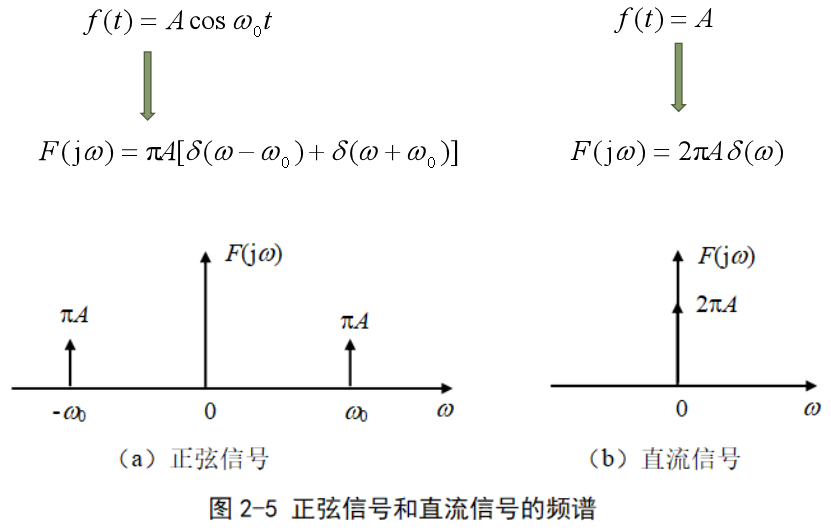
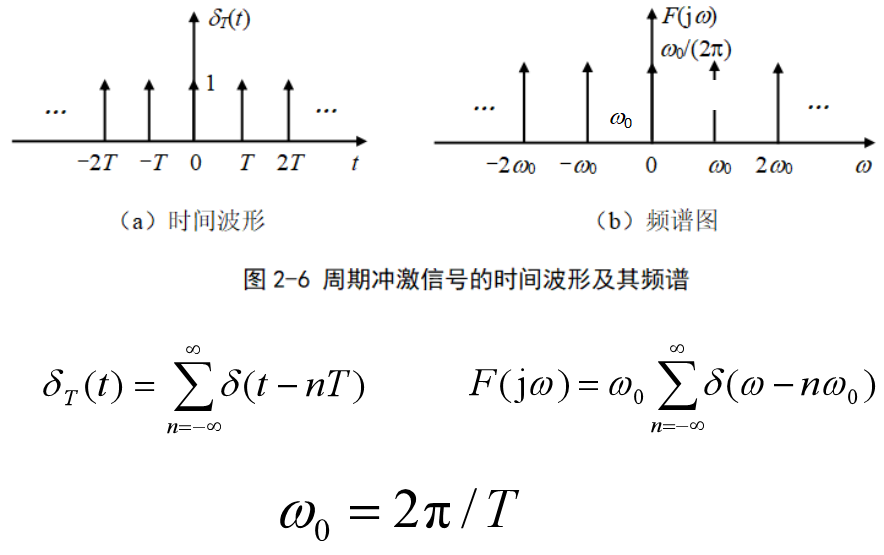
傅里葉變換的另一種形式
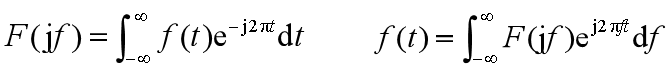
兩種形式之間的關系:
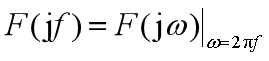
特別注意:對周期信號
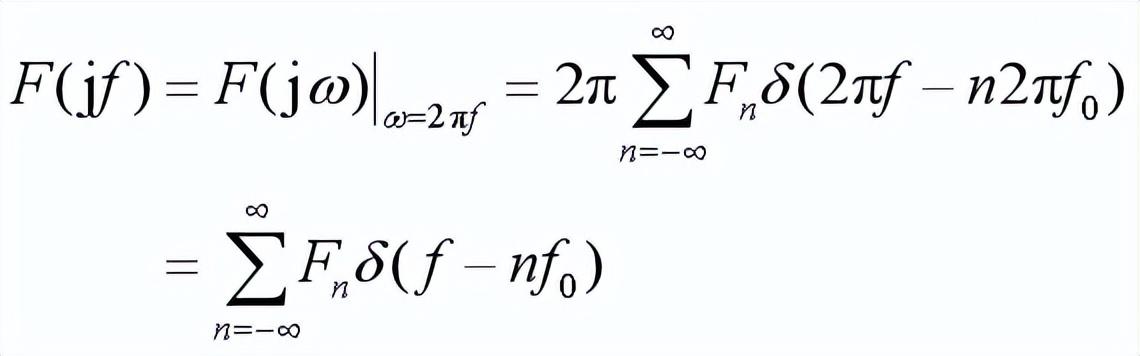
例如,周期沖激信號——
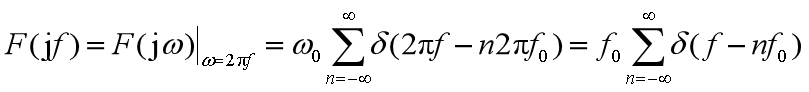
2.2 傅里葉變換的常用性質
時移性質
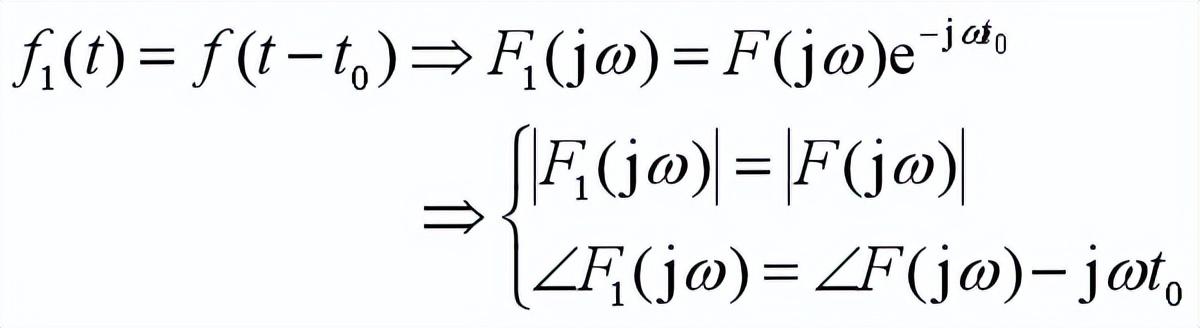
物理含義——
在時域,將信號沿著時間軸平移;
在頻域,信號的幅度譜將保持不變,只是相位譜有附加的相移-ωt?,即信號中的所有分量都將平移相同的時間t?。
尺度變換性質
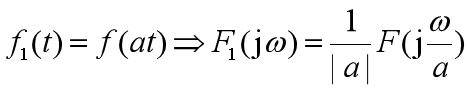
物理含義:
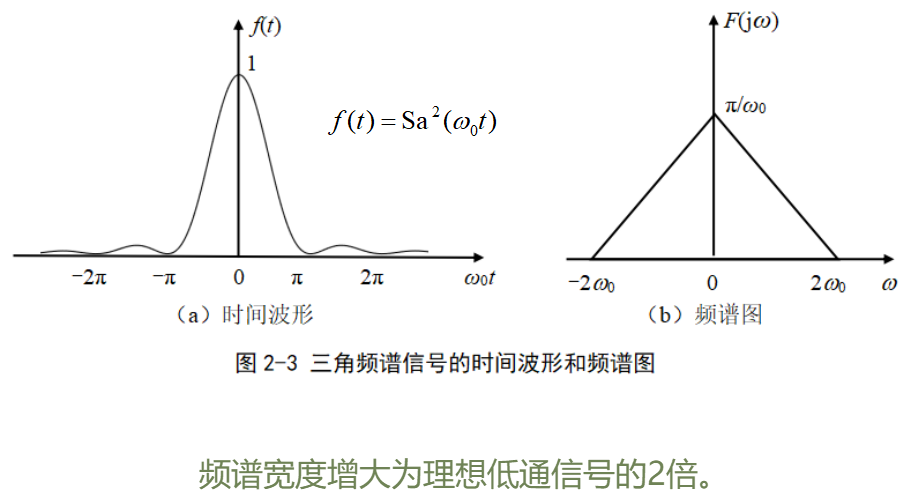
信號的時寬與帶寬成反比。
在時域增加信號的持續時間,則信號的頻譜寬度將得到壓縮;
反之,減小信號持續的時間,信號的頻譜寬度將增大。
在通信系統中,要求以更快地的速度傳輸信號,相當于將信號在時域中進行壓縮,則信號的帶寬將增大,也就要求傳輸信道提供更大的帶寬。
頻移性質(調制定理)
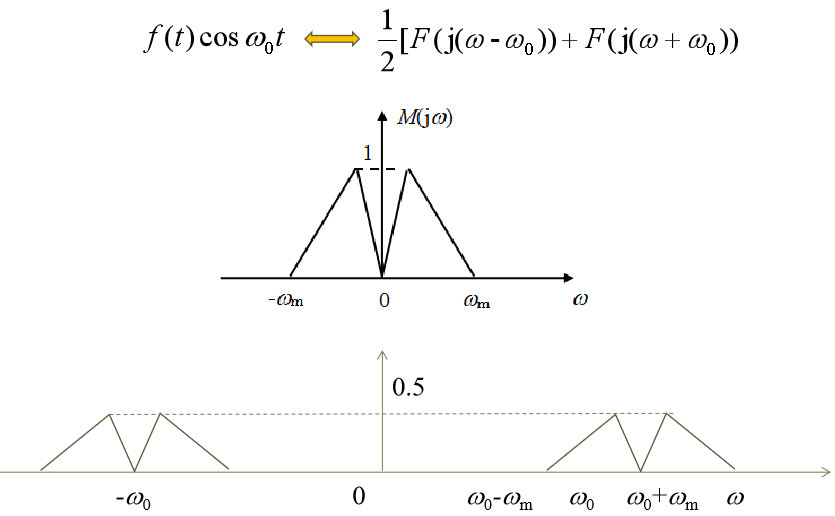
2.3 信號的能量譜、功率譜與自相關函數
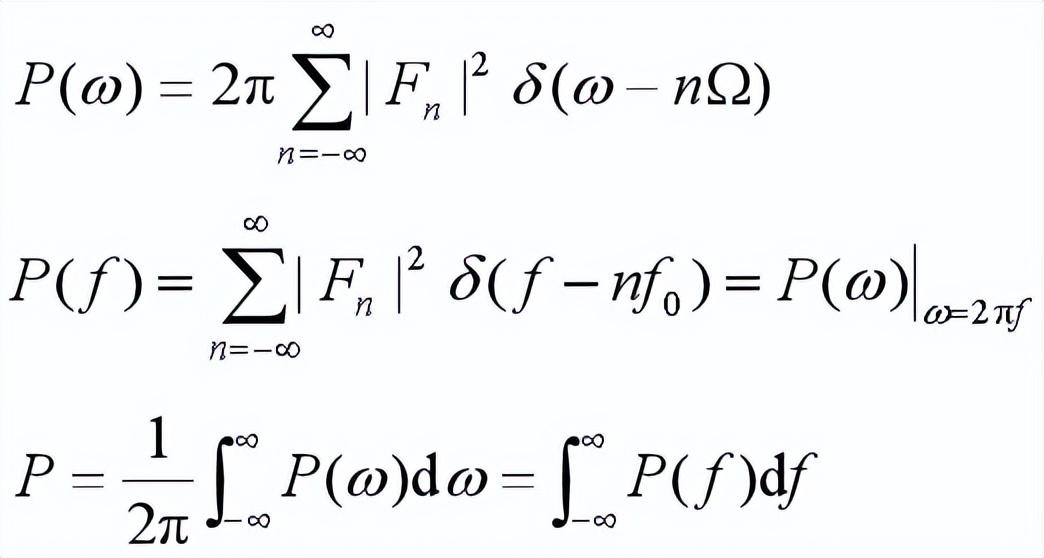
頻譜代表的是信號中各頻率分量的幅度和相位
功率譜代表的是信號中各分量的功率
信號的總功率等于各分量功率的和(連續和、積分)
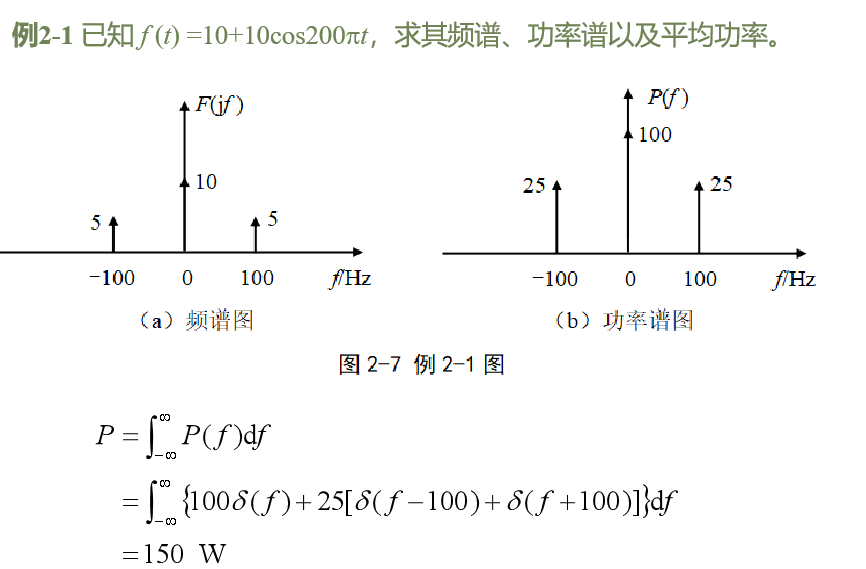
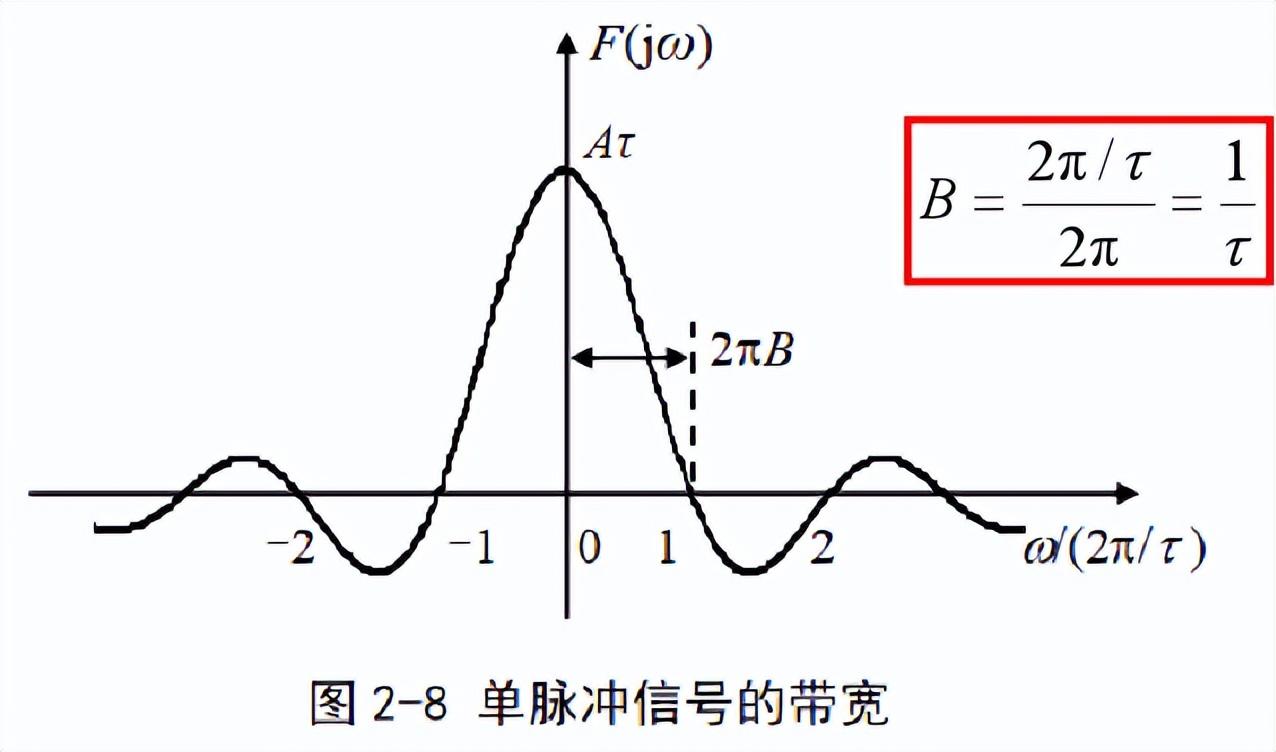
2.4 信號的帶寬
信號通過傅里葉變換分解為很多不同頻率正弦信號分量的疊加,信號的頻帶寬度B(簡稱為帶寬 Bandwidth)
定義為所有分量頻率的變化范圍,或者頻譜圖中右半平面不恒為0的部分在橫軸上的投影寬度,單位為Hz。
近似帶寬:
實際信號的頻譜都具有收斂性,各分量的幅度都將隨著頻率的增大而逐漸衰減。
超過一定頻率的分量,其幅度可以忽略,因此可將該頻率近似定義為信號的帶寬。
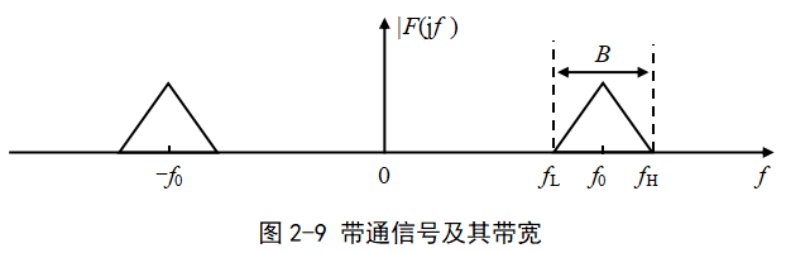
帶通信號的帶寬:
對通信系統中傳輸的各種已調信號,大都屬于帶通信號,也就是信號的頻譜位于某個較高的頻率 f? 附近,如圖2-9所示。
一般情況下,當
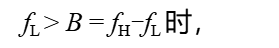
即可視為帶通信號。
3 線性系統與濾波器
3.1 線性系統及其頻率特性
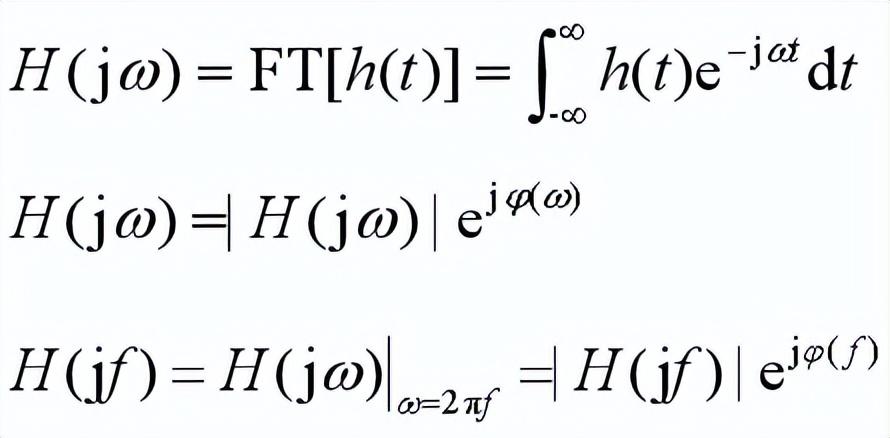
物理含義——
幅頻特性| H(jω)|或| H(jf )|代表信號通過系統傳輸時,
系統對其中各分量幅度的放大倍數,
而相頻特性φ(ω)或φ( f )代表信號中各分量相位和時間的延遲。
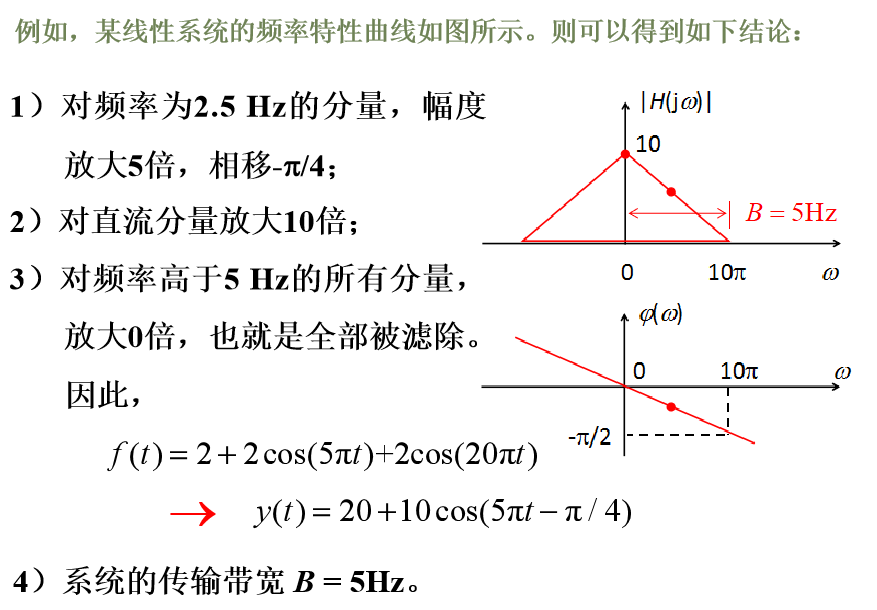
3.2 系統響應的頻域求解
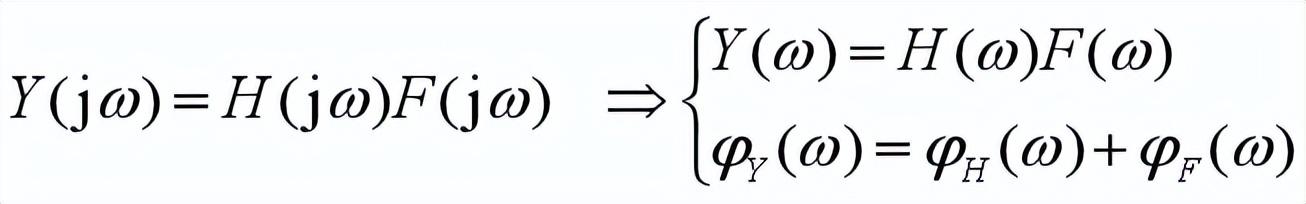
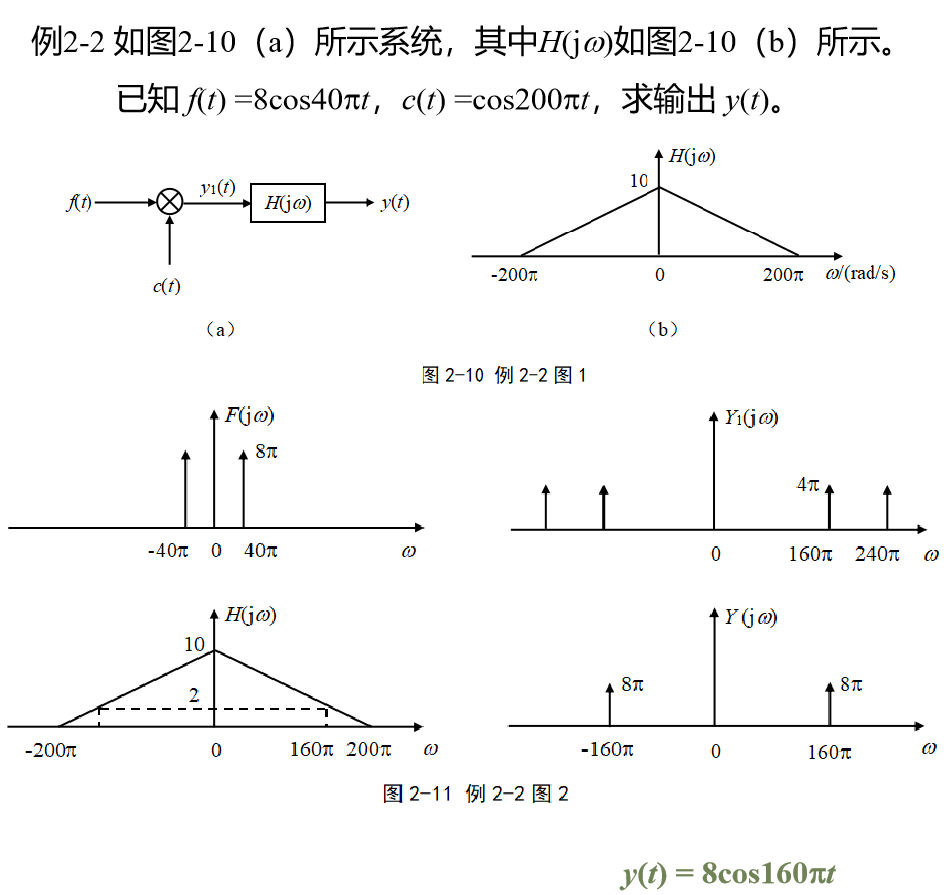
3.3 濾波器
系統的無失真傳輸
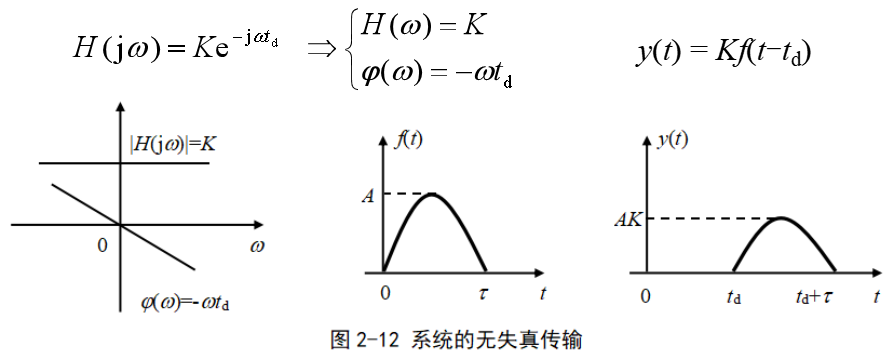
滿足上述條件的系統,帶寬為無窮大。
考慮到實際系統傳輸的信號帶寬有限,只要滿足系統帶寬不低于傳輸信號的帶寬,就近似認為傳輸沒有失真。
例數字信號通過不同帶寬的信道(濾波器):
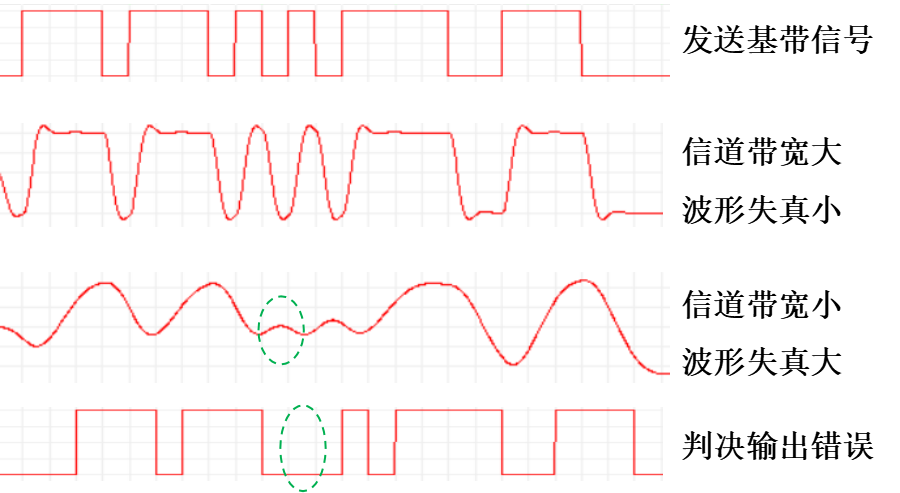
濾波器
信號通過系統時,有些分量被全部濾除,而另外一些分量能夠通過系統,
在系統的輸出信號中存在同頻率的分量。 具有這種特性的系統稱為濾波器。
根據幅頻特性,將理想濾波器分為四種基本類型,即
低通濾波器(LPF,Low Pass Filter)高通濾波器(HPF)帶通濾波器(BPF)帶阻濾波器(BSF)
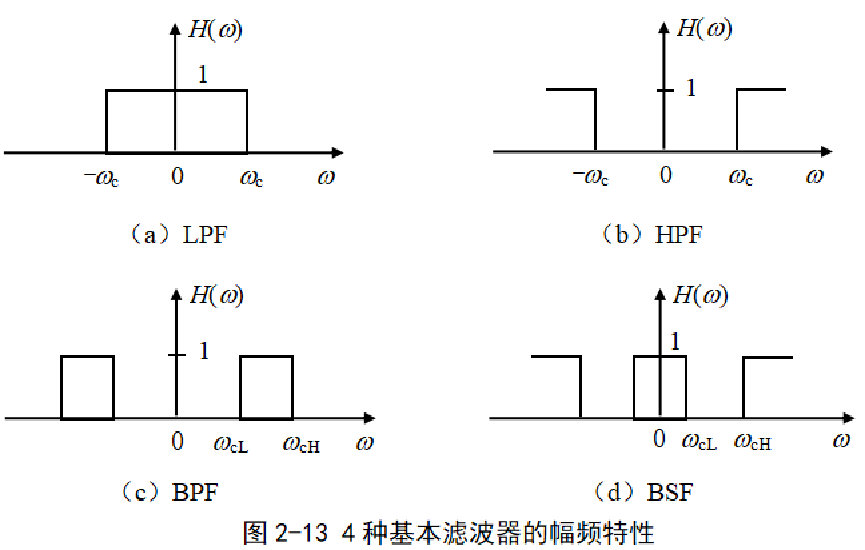
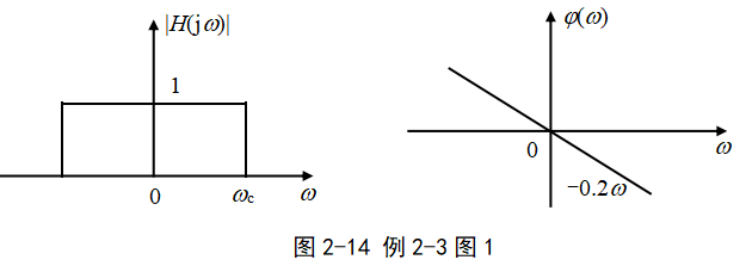
例2-3某理想LPF的頻率特性如圖2-14所示。 其中
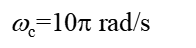
(1)求濾波器的單位沖激響應h(t)。
(2)求系統在f(t) = 5cos2πt +cos12πt作用下的輸出響應y(t)。
(3)為使上述信號通過濾波器后不失真,該如何調整濾波器的參數?
解
由于輸入信號中的兩個分量分別位于低通濾波器的通帶和阻帶內,因此只有低頻分量能夠通過低通濾波器,從而使得輸入輸出信號的波形有失真。 為避免失真,應該使輸入信號中的兩個分量都位于濾波器的通帶內。 因此,應將濾波器的截止頻率?c增大,并使之滿足?c >12? rad/s,即濾波器的帶寬至少應增大到6Hz。
希爾伯特濾波器
希爾伯特(Hilbert)濾波器是一個寬帶移相網絡,其幅頻特性具有全通特性,相頻特性對輸入信號中的所有頻率分量都移相-π/2。
2.4 信道及其特性
4.1 信道的分類
信道的分類
有線信道、無線信道;
模擬信道、數字信道;
調制信道、編碼信道
4.2 信道的數學模型
調制信道
至少有一個輸入端和一個輸出端;
大多數的調制信道都是線性的,可以視為一個濾波器;
傳輸過程中會有延遲和衰減;
傳輸過程中會引入噪聲,使得輸入端沒有信號時,信道的輸出端仍會有輸出噪聲。
編碼信道
傳輸過程可以認為是對數字序列的變換,即把一種數字序列變成另一種數字序列。 因此編碼信道是一種數字信道。
信號傳輸過程中,各種噪聲對編碼信道的影響,最終表現為數字序列的變化。 由于干擾的存在,編碼器輸出數字代碼序列通過信道傳送到譯碼器時,將使得譯碼輸出代碼序列發生錯誤。
4.3 信道特性對傳輸的影響
根據乘性干擾的性質,可以將調制信道分為恒參信道和隨參信道。
恒參信道的乘性干擾不隨時間變化或基本不變化,
隨參信道的乘性干擾是隨機變化的。
典型的恒參信道包括有線信道和部分無線信道。
由信道幅頻特性不理想而造成的失真稱為幅頻失真。如果用這種信道傳輸數字信號,將會引起相鄰碼元波形在時間上的相互重疊,造成碼間干擾。如果信道不具有理想的群延遲特性,將使得信號中的各分量有不同的延遲,從而引起合成波形發生畸變。這種由信道相頻特性不理想造成的失真稱為相頻失真。
5 噪聲
5.1 噪聲的來源及分類
噪聲的來源及分類
根據對信號產生作用和影響的方式,噪聲可以分為加性噪聲和乘性噪聲。
乘性噪聲對信號的影響是以相乘的形式出現,而加性噪聲與信號呈疊加關系。
通過對通信系統的精心設計,有些噪聲可以消除或者得到衰減。但仍有一些噪聲由于無法確切地預測其波形,所以無法消除其對有用信號傳輸的影響。這種不能預測的噪聲統稱為隨機噪聲。
隨機噪聲主要有熱噪聲、散彈噪聲以及宇宙噪聲等。這類噪聲大多屬于加性噪聲。
5.2 高斯噪聲和白噪聲
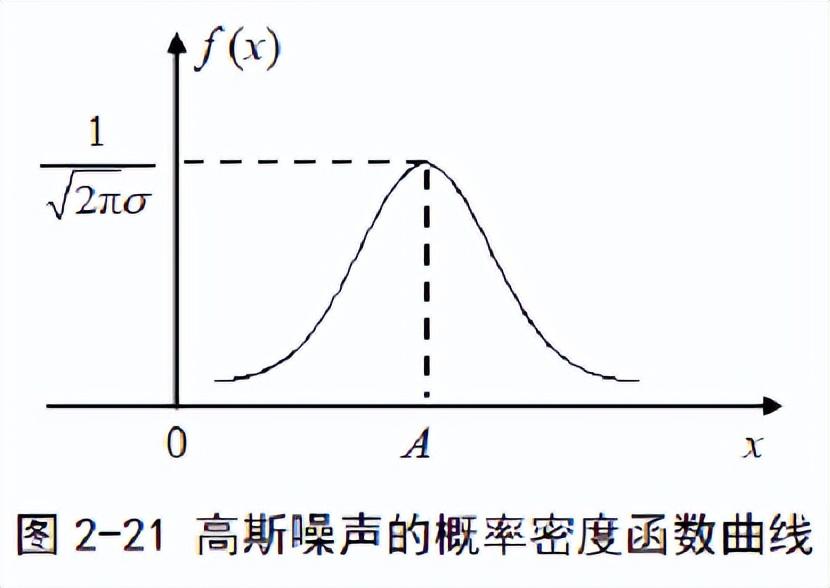
高斯噪聲
高斯噪聲在每個時刻的幅度瞬時值服從高斯分布,幅度概率密度函數可表示為:

白噪聲與帶限白噪聲
白噪聲的功率譜在整個頻率范圍為常數,即
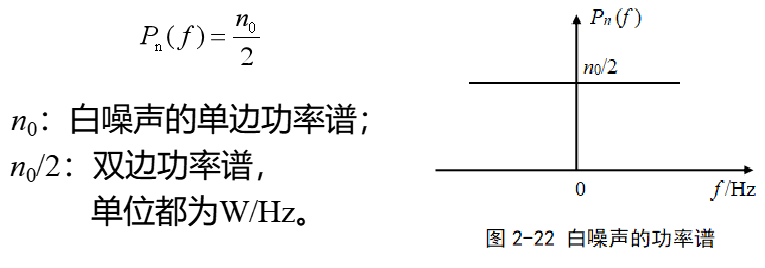
白噪聲通過帶寬有限的通信系統或濾波器后,頻帶將受到限制,這種白噪聲稱為帶限白噪聲。
根據系統和濾波器特性的不同,典型的帶限白噪聲又分為低通型和帶通型兩種。
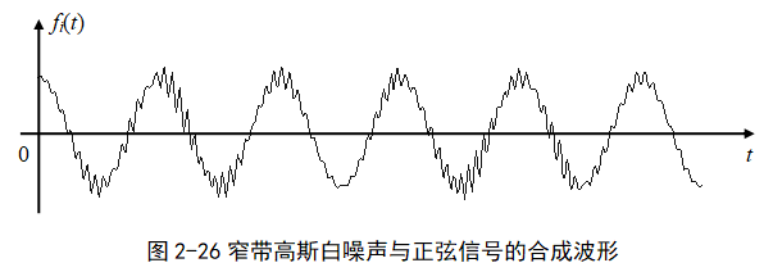
5.3 窄帶高斯白噪聲
時域和頻域特性
帶寬遠小于中心頻率(B << f0);
幅度服從高斯分布;
功率譜密度在帶寬范圍內為常數,而在帶外為0。
由于同相分量和正交分量具有相同的功率譜,因此其平均功率相同,即
窄帶高斯白噪聲與正弦波的疊加

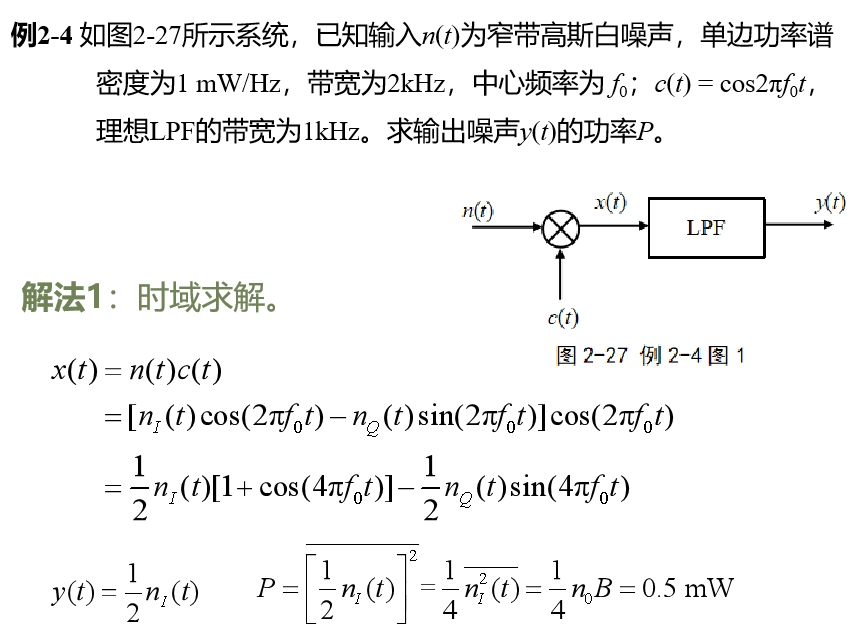
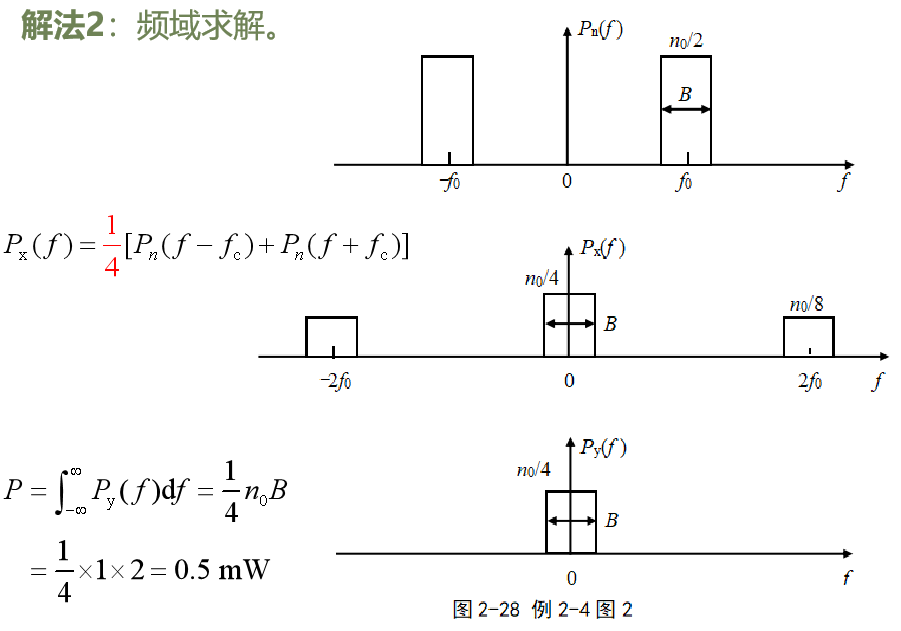
-
通信系統
+關注
關注
6文章
1193瀏覽量
53366 -
發射機
+關注
關注
7文章
505瀏覽量
48046 -
信號
+關注
關注
11文章
2792瀏覽量
76836 -
頻譜
+關注
關注
7文章
883瀏覽量
45661 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42617
發布評論請先 登錄
相關推薦




 傅里葉變換與信號的頻譜講解
傅里葉變換與信號的頻譜講解











評論