支持向量機(Support Vector Machine)是一種較知名的機器學習算法,該算法由俄羅斯數學家Vladimir Vapnik創立。
下文介紹支持向量機的基礎概念:線性可分的定義(二分類的線性可分定義)
一、基于二維特征空間感性認識對線性可分
(1)線性可分(Linear Separable)
如果訓練樣本集的特征空間如圖一所示,其中的圓圈和叉可被一條直線劃分,則該訓練樣本集為線性可分。 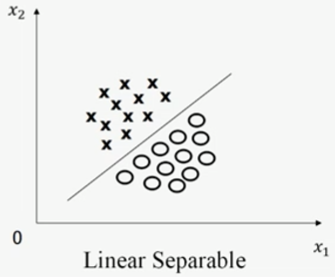
圖一,圖片來源:中國慕課大學《機器學習概論》
(2)線性不可分(Nonlinear Separable)
如果訓練樣本集的特征空間如圖二所示,其中的圓圈和叉不可被一條直線劃分,則該訓練樣本集為線性不可分。
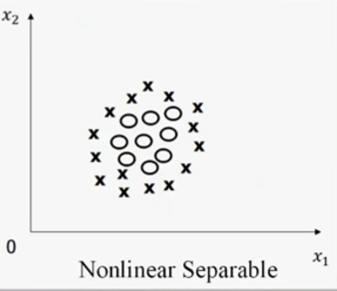
圖二,圖片來源:中國慕課大學《機器學習概論》
二、線性可分的定義
(1)二維特征空間下線性可分的定義 如圖三所示,二維特征空間的兩個維度分別為x1、x2,并假設該特征空間分布如圖三的訓練樣本,訓練樣本包括圓圈和叉,圓圈采用類別標簽C1表示,叉采用類別標簽C2表示。
基于以上假設,圖三特征空間中存在一條直線將訓練樣本分類為C1和C2,并假設該直線的方程為: ω1x1+ω2x2+b=0 其中,ω1和ω2分別為x1和x2的權重,b為偏置。
再規定:C1側空間由ω1x1+ω2x2+b>0表示,C2側空間由ω1x1+ω2x2+b<0表示(也可規定C1側空間由ω1x1+ω2x2+b<0表示,C2側空間由ω1x1+ω2x2+b>0表示)。
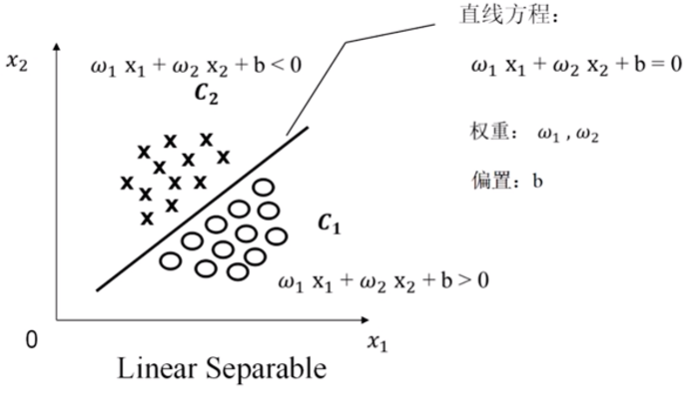
圖三,圖片來源:中國慕課大學《機器學習概論》
再假設N個訓練樣本的標簽為:{(X1,y1),(X2,y2),…,(XN,yN)},其中Xi=[xi1,xi2]T(二維特征空間每個訓練樣本只包含xi1,xi2兩個分量),yi={+1,-1},當Xi的類別標簽為C1時,yi的值為+1,當Xi的類別標簽為C2時,yi的值為-1(該規定可方便定義。也可規定當Xi的類別標簽為C1時,yi的值為-1,當Xi的類別標簽為C2時,yi的值為+1,±1也可被替換為絕對值不同的數字)。
基于以上假設和規定,二維特征空間的線性可分的定義如下: 一個訓練樣本集{(X1,y1),(X2,y2),…,(XN,yN)},在i=1~N線性可分是指存在(ω1,ω2,b),使得對i=1~N,有: 1)若yi=+1,則ω1x1+ω2x2+b>0 2)若yi=-1,則ω1x1+ω2x2+b<0 ?
二維特征空間線性可分向量形式的定義如下: 假設Xi=[xi1,xi2],ω=[ω1,ω2]T,那么: 若yi=+1,則ωTXi+b>0;若yi=-1,則ωTXi+b<0,即yi(ωTXi+b)>0。
(2)n維特征空間線性可分的定義(含個人理解)
根據二維特征空間線性可分向量形式的定義,可推廣至n維特征空間線性可分向量形式的定義:即假設Xi=[xi1,xi2,…,xin],ω=[ω1,ω2,…,ωn]T,那么一個n維訓練樣本集 {(Xi,yi)}在i=1~N線性可分是指存在ω和b,使得對 i=1~N,有yi(ωTXi+b)>0。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20873 -
機器學習
+關注
關注
66文章
8406瀏覽量
132567
原文標題:機器學習相關介紹(6)——支持向量機(線性可分定義)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
工控機支持什么操作系統
單片機驅動彩屏最簡方案:單片機_RA8889最小開發板驅動控制TFT彩屏介紹(一)
nlp自然語言處理基本概念及關鍵技術
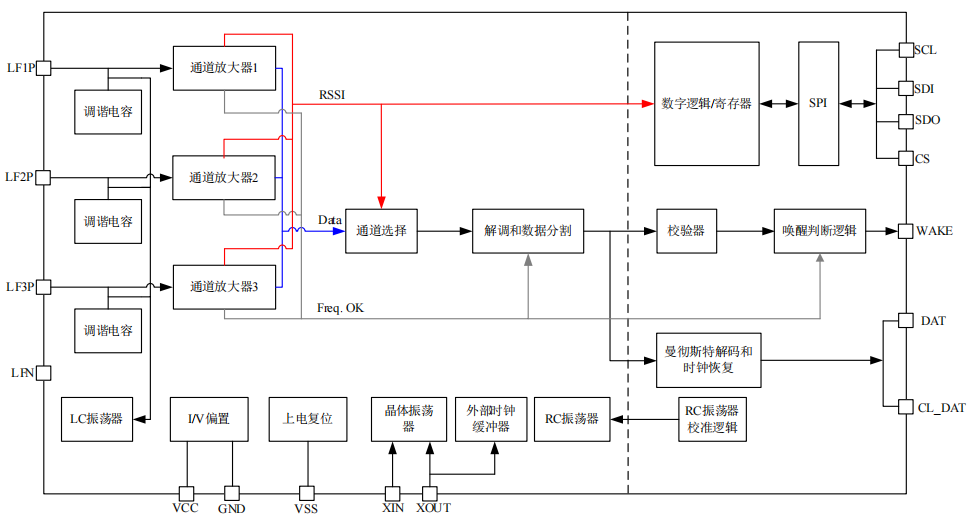
SI3933 是一款三通道的低功耗 ASK 接收機 125K頻段
請問STM8L052R8的USART2中斷向量在哪?
搭載英偉達GPU,全球領先的向量數據庫公司Zilliz發布Milvus2.4向量數據庫
什么是中斷向量偏移,為什么要做中斷向量偏移?




 介紹支持向量機的基礎概念
介紹支持向量機的基礎概念











評論