量子計算是一種基于量子效應的新型計算方式,它是以量子比特作為信息編碼和存儲的基本單元,通過大量量子比特的受控演化來完成計算任務。 以量子計算為基礎的信息處理技術的發展有望引發新的技術革命,為大數據和機器學習、人工智能、化學反應計算、材料設計、藥物合成等許多領域的研究,提供前所未有的強力手段,對未來社會的科技、經濟、金融,以及國防安全等產生革命性的影響。
本文以詞條形式主要介紹量子計算相關的術語,讓你對量子計算有個快速簡單的總覽。
量子計算的理論依據
疊加態Superposition 疊加態原理,是量子力學中的一個基本原理,它廣泛應用于量子力學各個方面,“薛定諤的貓”就是用來描述疊加態的經典比喻。在經典物理中,粒子任何時刻的狀態都是空間中一個固定的點。在量子力學中,粒子可以不處于一個固定的狀態(上或下),而是同時處于兩種狀態的疊加(上和下)。
量子糾纏
QuantumEntanglement
量子糾纏,它描述了粒子量子態之間的高度關聯,這樣的“關聯”可以是多種形式,比如自旋態總是相反,或總是相同,或者是既可能相反也可能相同,但相反的可能性比相同大。只要兩個粒子相互關聯構成疊加態,它們就會“互相糾纏”在一起,即使在兩個粒子分開到很遠很遠距離的情況下,它們能瞬間互相影響的“糾纏”照樣存在。這種關聯是經典粒子對沒有的,是僅發生于量子系統中的獨特現象。
量子測量
Measurement
量子測量是觀察量子態的行為,這種觀察將產生一些經典信息,該測量過程將改變量子態。例如狀態處于疊加狀態,則測量會將其“折疊”為經典狀態(0或1),坍縮過程是隨機發生的。在進行測量之前,無法知道結果如何,但是可以計算每個結果的概率,這個概率是對量子狀態的一種預測,可以通過多次準備狀態,對其進行測量然后計算每個結果的概率來測試該預測。
量子隧穿
Quantum Tunneling
量子隧穿是一種量子力學效應,指的是像電子等微觀粒子能夠穿入或穿越位勢壘的量子行為,盡管位勢壘的高度大于粒子的總能量。在經典力學里,這是不可能發生的,但使用量子力學理論卻可以給出合理解釋。在量子力學中,波函數表示粒子在特定位置的概率,這表明粒子存在位于障礙物另一側的概率。
貝爾不等式
Bell’s Inequality 最初的貝爾不等式是由愛爾蘭物理學家約翰·斯圖爾特·貝爾發現的,其他不等式現象后來被其他研究人員發現,貝爾的所有不等式加在一起便構成了貝爾定理。
貝爾證明了該術語的經典定義中的世界不符合當地的現實主義。“本地”意味著對象只能受到其周圍環境的影響。從物理學的意義上講,“現實主義”是指物體的性質在某人測量(甚至被測量)之前和之后都存在于人的思想之外。
經典力學說,在測量之前和之后,粒子具有真實的(確定的)值,取兩個相撞并相距很遠的粒子,一個人對另一個人的任何影響都必須立即通過“場”傳達出來(但絕不能比光速快)。
貝爾不等式是涉及光子自旋的理論實驗中的一系列測量,通過方向不同的檢測器進行測量。不平等是指這樣一個事實,即如果世界表現出局部真實性,則一組光子測量結果將大于另一組。然而事實并非如此,這意味著物理世界受量子力學理論支配,量子糾纏的啟示僅證實了這一觀點。
不可克隆性
No-Cloning Theorem
由于量子力學的態疊加原理和系統態的演化遵從幺正變換,使得任何量子體系的任意未知量子態無法被完全復制。即無法在不破壞原來未知態的情況下對之
玻色-愛因斯坦凝聚態
Bose-Einstein Condensate
玻色-愛因斯坦凝聚態是超冷原子云,華盛頓州立大學的研究員彼得·恩格斯(Peter Engels)解釋說:“這一大原子團的行為不像桶中的一堆球。它的行為就像一個大的超級原子。因此,它放大了量子力學的作用。”從理論上講,玻色-愛因斯坦凝聚物(BEC)可以充當穩定的量子比特。
布洛赫球
Bloch Sphere
在量子力學中,布洛赫球是二級量子力學系統(量子比特)的純態空間的幾何表示,以物理學家Felix Bloch命名。布洛赫球是一個單位球,其對映點對應于一對相互正交的狀態向量。布洛赫球提供了以下解釋:極點代表經典位,我們使用符號|0?和|1?。然而,盡管這些是經典位表示的唯一可能狀態,但量子比特覆蓋了整個球體。因此,量子比特中包含了更多的信息,布洛赫球對此進行了描述。當量子比特被測量時,它坍塌到兩個極點之一。這兩個極點中的哪一個取決于布洛赫表示中的箭頭指向哪個方向:如果箭頭更靠近北極,則更有可能塌陷到北極;南極也一樣。應當注意,這將概率的概念引入了布洛赫球體:箭頭與垂直軸的角度θ對應于該概率。如果箭頭指向赤道,則任一極都可能塌陷50-50。
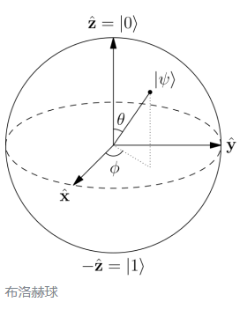
馬約拉納費米子
Majorana Fermions 形成物質的基本粒子(“費米子”)由保羅·狄拉克(Paul Dirac)于1928年提出的方程式Dirac方程來描述,這意味著宇宙中的每個基本粒子都有一個反粒子,其質量相同但電荷相反。1932年發現了第一個反粒子,與電子結合的正電子。電子和其他基本粒子具有不同的反粒子,它們通過希格斯機制獲得質量,在物理學中,它們被稱為“狄拉克費米子”。
1937年,意大利物理學家埃托爾·馬若拉納(Ettore Majorana)發現了一個更通用的方程式(Majorana Equation),該方程式預測了中性費米子的存在(不帶電荷)是它們自己的反粒子。Majorana費米子是特殊的粒子,因為它們不是通過希格斯機制獲得質量而是與其自身相互作用而獲得質量,因此它們是自己的反粒子。
自旋
Spin 自旋有時稱為“核自旋”或“本征自旋”,這是基本粒子、復合粒子(強子)和原子核所攜帶的角動量的量子形式。旋轉與實際旋轉無關,物理學家使用“自旋”或“內在自旋”一詞來區分粒子“有點”具有的角動量和物理旋轉物體的規則角動量。 量子算法
量子算法
Quantum Algorithm
算法是指令的集合,允許計算函數,例如數字的平方。一個量子算法允許指令進行疊加,并創建糾纏,這使得量子算法可以完成某些常規算法無法完成的事情。
大數因子分解的Shor量子算法
Shor's quantum algorithm for large number factorization
1994年,貝爾實驗室計算機科學家SHORP發表了一種快速進行因數分解的方法,算法利用量子計算的并行性,對任意大的整數快速做因數分解,大大降低了當前普遍使用的RSA公開密鑰加密技術的破解時間。Shor算法包含兩個部分:一個以傳統的電腦運作的簡化算法,將因子分解簡化成搜尋目的問題,使用輾轉相除法計算gcd(a,N);一個量子算法,解決搜尋目的問題。
Grover算法
Grover Algorithm
1996年,貝爾實驗室的Grover提出一種通用的搜索破譯算法,其計算復雜度為O().對于密碼破譯來說,這一算法的作用相當于把密碼的密鑰長度減少到原來的一半。Grover算法已經對現有密碼構成很大的威脅,但是并未構成本質的威脅,因為只要把密鑰加長1倍就可以了。
量子隨機游走Quantum Random Walk
隨機游走以及馬氏鏈是一種非常強大的經典算法設計技術,被廣泛的應用到搜索問題、采樣問題以及近似估計。同樣地,量子隨機游走也為量子算法設計提供了一種一般化的框架。與經典的隨機游走不同,給定了一個圖結構,量子隨機游走算法按照量子的機制(酉變換)在圖結構上模擬粒子的行為。相比于經典隨機游走,量子隨機游走一般具有更快的首達時間。對于一些特殊的圖,量子隨機游走的首達時間可以比經典隨機游走的首達時間指數量級的小。另外量子隨機游走有著更快的混合時間。
求解線性方程組的量子算法
Quantum Algorithm for linear systems of equations
解線性方程組是一個基本的數學問題,在工程等領域有著重要應用。2008年Harrow等提出了一種可以在對數時間內求解線性方程組的量子算法(HHL算法)。學者們已經將HHL算法推廣到機器學習領域,另外HHL算法還可應用于有限元方法,2013年Clader等提出了一種利用HHL算法解決電磁散射問題的有限元方法。
絕熱優化算法Adiabatic Quantum Optimization
絕熱優化是指采用絕熱計算的方法來求解最大約束滿足問題。Farhi等提出了使用絕熱計算來求解最大約束滿足問題的算法:系統先制備一個簡單的Hamilton量并使其處于基態,然后緩慢地讓系統進行絕熱演化,使其演化為一個復雜的Hamilton量,這個Hamilton量的基態編碼了最大約束滿足問題的解。如果這個演化過程進行得足夠慢,那么量子絕熱定理就能保證系統一直處于基態,最后的狀態也一定就是優化問題的解。
量子計算的物理實現
DiVincenzo標準
DiVincenzo Criteria
DiVincenzo標準是構建量子計算機的必要條件,他們首先由理論物理學家David DiVincenzo在2000年提出“量子計算的物理實現”。DiVincenzo標準由實驗設置必須滿足5+2個條件組成,才能成功實現量子算法,例如Grover的搜索算法或Shor因式分解。實現量子通信需要兩個附加條件,例如量子密鑰分發中使用的條件。
1. 具有特征明確的量子比特的可擴展物理系統。
2. 將量子比特的狀態初始化為簡單基準狀態的能力。
3. 較長的相關退相干時間。
4. 一組“通用”量子門。
5. 特定于量子比特的測量功能。
6. 交換固定和飛行量子比特的能力。
7. 在指定位置之間忠實傳輸飛行量子比特的能力。
超導量子計算
Superconducting Quantum Computation 超導量子計算的核心單元是一種“超導體-絕緣體-超導體”三層結構的約瑟夫森結電子器件,其中間絕緣層的厚度不超過10nm,形成一個勢壘,庫珀對能夠隧穿該勢壘形成超導電流。
與天然的量子體系相比,超導量子電路的能級結構可通過對電路的設計進行定制,或通過外加電磁信號進行調控。而且,基于現有的集成電路工藝,約瑟夫森量子電路還具有天然量子體系無法比擬的可擴展性。這些優點使超導量子電路成為實現可擴展量子計算最有前景的物理方案之一。超導量子計算存在的主要問題是固體體系中大量不易操控的自由度給約瑟夫森量子電路帶來強烈的消相干,其中最典型的消相干過程是由具有低頻特性的電荷型或磁通型偏置噪聲所導致的退相干。
離子阱量子計算
Trapped Ion Quantum Computation 1995年,Cirac和Zoller首次提出在線性離子阱體系中實現量子計算,并于同年在實驗室中實現了該方案。在該體系中,Qubit是束縛在線性離子阱中單個離子的兩個內能級。單Qubit的幺正變換可以通過尋址激光束與單個離子的共振相互作用來完成,2個Qubit的受控幺正變換需要利用失諧的激光束先后照射兩個需要相互作用的離子,借助與整體離子串的聲子相互作用來完成。
離子阱方案的主要優點是阱中的超冷離子處于一個幾乎與外界隔絕的空間中,由環境引起的消相干效應非常小,因此使得量子計算的并行度較高,離子阱作為實現小規模量子計算機的強力候選被廣泛關注;其主要缺點是時鐘速度太慢,用數目極大的激光束脈沖操作各個離子執行邏輯運算時,運算速度難以提高。
量子點量子計算
Quantum Dot Computation 量子點量子計算使用半導體量子點中的電子自旋作為量子比特。量子點是一種有著三維量子強束縛的半導體異質結結構,其中電子的能級是分立的,類似于電子在原子中的能級結構,因此被稱為“人造原子”。量子比特編碼在電子的自旋態上,使用微波脈沖或者純電學的方法進行單量子比特操控,兩量子比特邏輯門可以通過半導體腔引入的相互作用或者相鄰量子點之間的電偶極相互作用來實現。
量子點方案的優點則是量子位可以是嵌套在固體材料中的固態量子器件,這與經典計算機的大規模集成電路的設計相似。半導體量子點的實現方式被認為是最有可能實現大規模量子計算機的候選方案。同時,由于與當前半導體工藝的良好兼容性,半導體量子點也成為量子計算研究領域發展最快的分支之一。另一方面半導體量子點體系受周邊環境的影響比較嚴重,控制其退相干,維持其量子相干狀態遇到了更大的挑戰。
拓撲量子計算
Topological Quantum Computation
拓撲量子計算建立在全新的計算思路之上,應用任意子的交換相位,交換過程的“編辮”程序實現量子計算的信息處理。拓撲學研究幾何形象在幾何元素的連續變形下保持變的性質。如果構成量子比特的元素是拓撲不變的,基于這些量子比特的運算結果也具有拓撲不變性。由此構造的量子計算對環境干擾、噪音、雜質有很大的抵抗能力。但拓撲量子計算尚停留在理論層面,實際上還未把這些理論付諸成器件化的現實。
核磁共振量子計算
NMR Quantum Computation 核磁共振量子計算使用核的自旋態作為量子比特。根據樣品的不同,它分為液體核磁共振量子計算和固體核磁共振量子計算。液體核磁共振使用溶于液體的分子上的核自旋作為量子比特通過共振頻率的不同來區分量子比特。使用與核自旋共振的射頻脈沖操控量子比特,核自旋之間的交換相互作用用來實現量子比特間的糾纏和兩量子比特邏輯門。
由于環境相對簡單,核自旋擁有較長的退相干時間。基于核磁共振的量子調控技術也是相對比較成熟的技術。基于這些優勢,液體核磁共振量子計算是目前所有實驗物理體系中進展最好的,并且成為了驗證量子計算原理和各種模型的絕佳實驗平臺。
光量子計算
Optical Quantum Computation 量子比特的光子實現在量子信息科學中扮演著重要的角色,除了在量子密碼和量子通信中非常成功的應用之外,光子量子計算也是最初實現多粒子糾纏,量子態的制備,簡單量子算法的物理系統之一。光子所具有的巨大的優點在于它沒有退相干,并且我們可以精確的控制和操縱它。光子量子計算吸引人們的另一點是它可以與各種量子通信的應用緊密聯系在一起,比如可以用它來做分布式量子計算。 量子計算機的構成
量子比特
Qubit 在常規計算機中,信息單元用二進制的1個位來表示,它不是處于“0”態就是處于“1”態。在二進制量子計算機中,信息單元稱為量子比特(qubit),它除了處于“0”態或“1”態外,還可處于疊加態(superposedstate)。疊加態是“0”態和“1”態的任意線性疊加,它既可以是“0”態又可以是“1”態,“0”態和“1”態各以一定的概率同時存在。
簡單來說,量子比特就是一個具有兩個量子態的物理系統,如光子的兩個偏振態、電子的兩個自旋態、離子(原子)的兩個能級等都可構成量子比特的兩個狀態。
Transmon
Transmon是一種超導環形量子比特,可以在極低的溫度下創建,目前最多可以將其中五個鏈接在一起。標準的transmon可以保持大約50微秒的相干性,可以在量子電路中使用。更重要的是,相干時間是長度的兩倍,transmon數組包含10到20個循環。
Xmon
Xmon是由加利福尼亞大學圣塔芭芭拉分校的一個團隊創建的十字形量子比特。研究小組發現,通過將五個Xmon放在同一行中,他們能夠創建穩定有效的量子排列,從而提供最大的穩定性和最少的誤差。像大多數其他量子比特一樣,必須在接近絕對零的溫度下創建Xmon。
拓撲量子比特
Topological Qubit
量子比特非常挑剔,即便是最輕微的擾亂,它們也會“散開”,不再可用于計算。引入拓撲量子比特概念,使其更加穩定,且能提供更多固有的防錯能力。根據定義,粒子的拓撲狀態就是粒子可被分解、并出現在系統不同地方的狀態。一旦粒子被分解,就很難被干擾,因為必須改變所有存儲在不同地方的信息。
量子寄存器
Quantum Register
n個量子位的有序集合稱為n位量子寄存器。它的態是n個量子位的態的張量積(tensor product)。n位量子寄存器可以存儲2n個n位數。
量子邏輯門
Quantum Logical Gates
對量子位的態進行變換,可以實現某些邏輯功能。變換所起的作用相當于邏輯門所起的作用,在一定的時間間隔內實現邏輯變換的量子裝置稱為量子邏輯門。與傳統邏輯門不同,量子邏輯門是可逆的。量子邏輯門是量子計算與量子計算機實現的基礎,可用下列方法實現:
(1)量子點系統;
(2)超導約瑟夫森(Josephson)結系統;
(3)核磁共振量子系統;
(4)離子阱系統;
(5)腔量子電動力學系統等。
量子邏輯網
Quantum Logical Nets
量子邏輯網絡由多個量子邏輯門組成,這些量子邏輯門的操作在時間上同步。
隨機基準
Randomized Benchmarking
一種用于確定一組量子門的平均錯誤率的實驗技術,這涉及到應用隨機電路,如果門無法正常工作,將產生零影響。基準測試是評估多量子比特量子計算機性能的重要程序。
量子存儲狀態
Quantum Memory State
量子存儲狀態是量子位在其中維持大量狀態以在量子計算中具有價值的狀態。迄今為止,這些狀態已被證明是非常脆弱的,因為在量子級的最小干擾就可以破壞它們。因此,大多數使用量子比特的實驗都要求將粒子冷卻到接近零的絕對值。
量子程序
Quantum Programs
量子程序的邏輯體系一般由“經典控制部分+量子數據部分”構成。量子程序的計算操作一般由以下三部分組成:
(1)一個初化操作,包括量子變量數據的初化; (2)一系列的酉變換;
(3)一個最終的測量。
量子計算機的組織結構
The organization of a quantum computer
量子計算機的計算過程由算法決定,不同的算法有不同的幺正變換。量子計算機的計算過程可由常規計算機控制,由于量子計算的測量結果是概率性的,需要計算和測量多次,才能得到所需結果。量子并行是量子計算機的特點,對于串行計算及迭代運算,量子計算機不具備優勢。量子計算機適合于作為常規的通用計算機的高速協處理器或外圍專用處理機,或專門為實現某種量子算法或模擬某種量子系統的專用計算機。
量子計算機的程序語言
The programming language of a quantum computer
與經典計算機類似,為便于控制并通用量子計算機,必須通過量子計算機設計語言來描述待解決問題,因此量子計算機程序設計語言將作為未來通用量子計算機上的一種重要系統軟件。現有量子算法一般固化于專用量子計算設備中,如果需要改變量子算法就必須重新設計量子計算設備,實際上,這就相當于一臺求解特定具體問題(不是一類特定問題)的專用計算設備。
量子模擬器
Quantum Simulator
量子模擬在很大程度上起源于理查德·費曼(Richard Feynman)的1982年的提議,現已發展成為科學家使用可控量子系統研究在實驗上不太可行的量子現象的領域。簡而言之,現在尚不存在完整的量子計算機,并且經典計算機通常無法解決量子問題,因此“量子模擬器”提供了一種吸引人的替代方法,可以深入了解例如復雜的材料特性。
通用量子計算機
Universal Quantum Computer 量子圖靈機(QTM),也是一種通用量子計算機,是用于量子計算機的效果進行建模抽象機。它提供了一個非常簡單的模型,可以捕獲量子計算的所有功能。任何量子算法都可以形式上表示為特定的量子圖靈機。牛津大學物理學家戴維·德意志(David Deutsch)在1985年的一篇文章中首次提出了這樣的圖靈機,該論文提出量子門的功能可以與傳統的數字計算二進制邏輯門類似。量子圖靈機并不總是用于分析量子計算。量子電路是更常見的模型,這些模型在計算上是等效的。 量子計算機的分類
當前,量子計算機可大致分為三類:量子退火、嘈雜中型量子(NISQ)計算、容錯型通用量子計算。
量子退火Quantum Annealing
絕熱量子計算機中用于解決優化和采樣問題的算法。它通過允許量子系統找到其最低能量狀態而起作用。在數據波動的情況下,量子比特位于最低的能量峰值上。這些都將量子比特控制和降低到零,最終得到了解決方案。
NISQ
NISQ是“Noisy Intermediate-Scale Quantum”的縮寫,它是指“嘈雜中等規模量子“。“中等規模”指的是現在可以獲得的量子計算機的尺寸大小———可能大到足以執行某些高度專業化的任務 ( 如新藥和新材料的設計等) ,超出了當今超級計算機的能力范圍。“嘈雜”則強調對量子比特的控制還不是非常完美,這將導致小誤差隨時間不斷積累,如果計算時間太長,就得不到正確答案。
容錯量子計算Fault-tolerant Quantum Computing 量子糾錯碼可以用來解決退相干等硬件的不完美導致的計算錯誤問題。在錯誤的分布滿足某些條件的情況下,我們可以把最終計算結果出錯的概率降得任意低,這被稱作容錯量子計算。量子糾錯是有代價的,為了降低最終出錯率,需要使用很多的量子比特來進行編碼。進行容錯量子計算的首要條件,也就是錯誤率低于容錯閾值(亞閾值)的初始化、量子門以及讀取等操作已經能夠在實驗中被演示。 其他
量子互聯網Quantum Internet
荷蘭QuTech的研究人員正在嘗試建立世界上第一個量子互聯網。量子互聯網就像普通的互聯網一樣,但是它可以發送量子態并建立糾纏。當然,建立全面的量子互聯網非常困難。因此,他們將在2020年之前建立一個小型的四節點網絡。該四節點網絡將作為大型網絡的測試平臺。該網絡的四個節點將是荷蘭的四個城市:代爾夫特,阿姆斯特丹,萊頓和海牙。
量子霸權
Quantum Supremacy
量子霸權是指量子計算擁有的超越所有經典計算機的計算能力。在物理實驗上,迄今還沒有任何一臺量子裝置在實際實驗中展現出這種能力。2019年9月20日,科技巨頭谷歌(Google)一份內部研究報告顯示,其研發的量子計算機成功在3分20秒時間內,完成傳統計算機需1萬年時間處理的問題,并聲稱是全球首次實現“量子霸權”。
相干時間
CoherenceTime
相干時間是量子疊加態可以存在的時間長度。
保真度
Fidelity
量子保真度不是指密度矩陣中包含的空間,而是指兩個量子態彼此接近程度的度量或精度,其中最簡單的例子是兩個量子位。通道保真度是衡量信息在通道內保留程度的一種度量,并且與量子保真度有關。
退相干
Decoherence
量子計算所需的量子門是幺正變換。在量子力學理論中,幺正變換描述了一個封閉系統的演化。然而,在自然界中我們還沒有發現真正的封閉系統:一個物理系統總是或多或少地與外界環境存在相互作用。由于相互作用的影響,系統演化不僅由系統本身決定還取決于環境的狀態。其結果是系統演化一般不再是幺正變換。有些非幺正演化會使量子系統逐漸失去相干性,也就是量子疊加態無法持續,這個過程被稱為退相干。退相干會導致量子算法失去優勢。
量子糾錯
Quantum Error Correction 量子計算機總是與環境相聯系,這種環境會干擾系統的計算狀態,從而導致信息丟失。量子糾錯通過獲取系統的計算狀態并將其分散到糾纏態上的量子比特上來解決這一損失。這種糾纏允許外部經典觀察者觀察和補救干擾,而不是觀察計算狀態本身,這將使它發生坍縮效應。
絕對零度
Absolute Zero
絕對零度是理論上可能的最低溫度,在該溫度下粒子的運動將最小。絕度零度在開爾文刻度上為零,等于–273.15℃。為了增加穩定性,大多數量子計算系統在接近絕對零度的溫度下運行。
摻雜金剛石
Doped Diamonds
對金剛石的量子應用集中在識別可以在碳晶格中發現的數百種不同缺陷。物理學家發現,他們可以充分利用這些缺陷來操縱量子粒子的自旋。
容錯材料
Fault-tolerantMaterial
容錯材料是一類獨特的高級材料,其內部電絕緣但在表面導電。在拓撲絕緣體的表面上誘導高溫超導性為創建容錯量子計算的先決條件打開了大門。這些材料之一是石墨烯,石墨烯的邊緣可將其轉變為一種可用于量子計算機的拓撲絕緣體。
量子點
Quantum Dot 量子點實際上是“人造原子”。它們是半導體的納米晶體,其中可以捕獲電子空穴對,納米晶體尺寸與光的波長相當,因此就像在原子中一樣,電子可以占據離散的能級,由此可以將點限制在光子晶體腔中,在此處可以用激光探測它們。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4620瀏覽量
93046 -
量子力學
+關注
關注
8文章
101瀏覽量
20115 -
量子計算
+關注
關注
4文章
1105瀏覽量
34965
原文標題:50個關鍵詞,帶你全面了解量子計算
文章出處:【微信號:Imgtec,微信公眾號:Imagination Tech】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
TF-IDF測量文章的關鍵詞相關性研究
HanLP關鍵詞提取算法分析詳解
關鍵詞優化有哪些實用的方法
#2023,你的 FPGA 年度關鍵詞是什么? #
基于強度熵解決中文關鍵詞識別
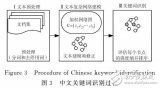
基于詞頻統計的關鍵詞提取方法
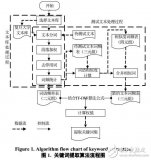
基于自動關鍵詞抽取方法
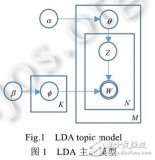
三大“關鍵詞”來了解AI
2020年云計算發展六大關鍵詞,以及六大關鍵詞背后的重要趨勢

融合BERT詞向量與TextRank的關鍵詞抽取方法




 50個關鍵詞,帶你全面了解量子計算
50個關鍵詞,帶你全面了解量子計算











評論