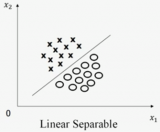
在Vladimir Vapnik創立支持向量機前,已有如下結論:在二分類情況中,如果一個數據集線性可分,即存在一個超平面可將兩個類別完全分開,那么一定存在無數個超平面將這兩個類別完全分開。
在特征空間為二維平面時,分類訓練數據的超平面的具體圖形為直線,下文介紹在無數個此類直線中選擇可使分類效果最優的直線。
一、直觀感覺分類效果最優的直線
如圖一左圖所示,有三條直線可將圖一左圖中的圓圈和叉分為兩類,該三條直線分別為1號線、2號線、3號線。在選擇可使圓圈和叉分類效果最優的直線(下文簡稱“最優分類直線”)時,可能多數人會選擇2號線。但根據免費午餐定理,在未假設訓練數據的先驗分布的情況下,三條直線對于圓圈和叉分類效果相同。人的直觀感覺似乎和免費午餐定理產生矛盾。
其實,似乎矛盾的原因是人們在選擇最優分類直線時,已對訓練樣本的先驗分布做出假設。例如,多數人選擇2號線為最優分類直線可能的假設為訓練樣本的位置在空間中具有測量誤差(選擇2號線為最優分類直線的先驗分布假設不唯一)。
如圖一右圖所示,如果紅色實線圓圈的位置分布具有測量誤差,其實際位置處于虛線圓圈位置,那么1號線的分類效果不如2號線的分類效果;如果紅色叉的位置分布具有測量誤差,其實際位置處于虛線圓圈位置,那么3號線的分類效果不如2號線的分類效果,即2號線更可抵御訓練樣本誤差,因此,在訓練樣本的位置在空間中具有測量誤差的先驗假設下,2號線為最優分類直線。 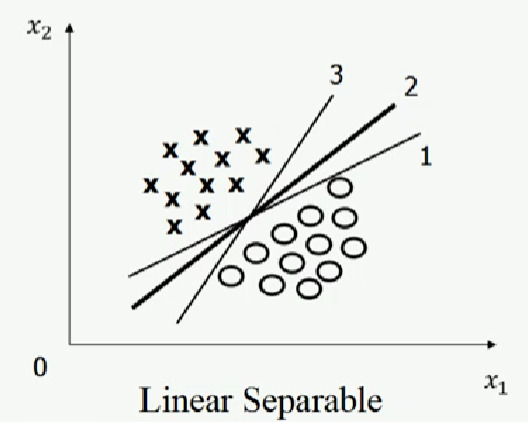
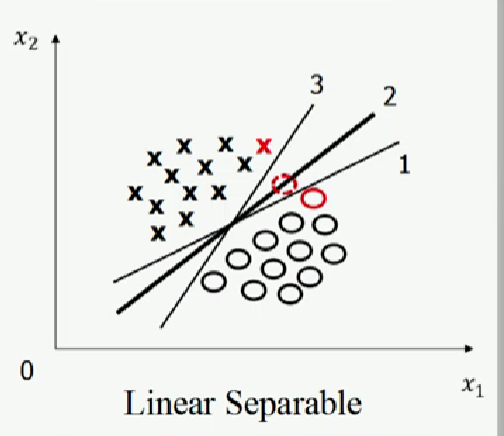
圖一,圖片來源:中國慕課大學《機器學習概論》
二、尋找最優分類直線
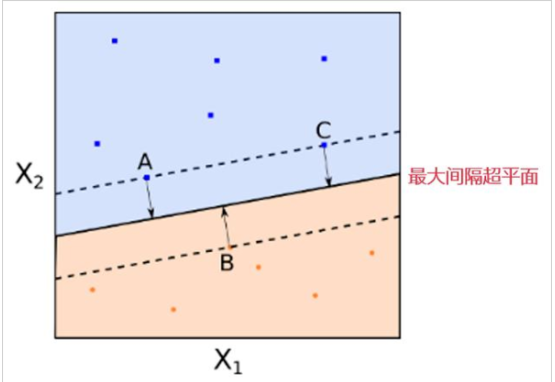
Vladimir Vapnik基于最優化理論,對尋找最優分類直線的回答如下:任意一條可將圓圈和叉完全分類的直線向一側平行移動,直至其穿過一側一個或幾個訓練樣本;再向另一側平行移動,直至其穿過另一側一個或幾個訓練樣本。如圖二所示,定義被穿過的數據(圖二中的紅圓圈和叉)為支持向量(Support Vector),定義穿過圓圈和叉的直線間的距離為間隔,則最優分類直線為間隔最大的直線。
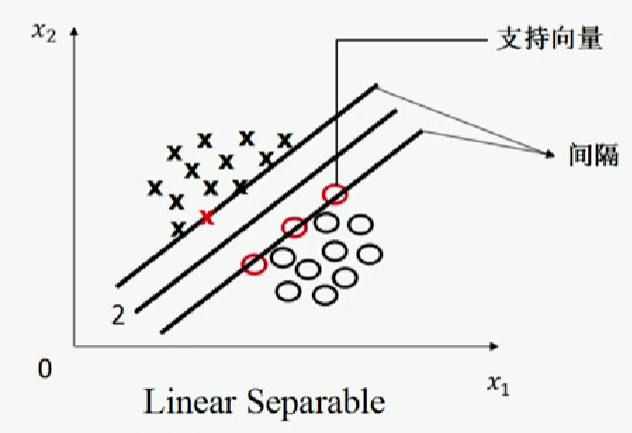
圖二,圖片來源:中國慕課大學《機器學習概論》
根據Vladimir Vapnik的回答,因為前文所述問題中的2號線的間隔最大,所以2號線為最優分類直線。 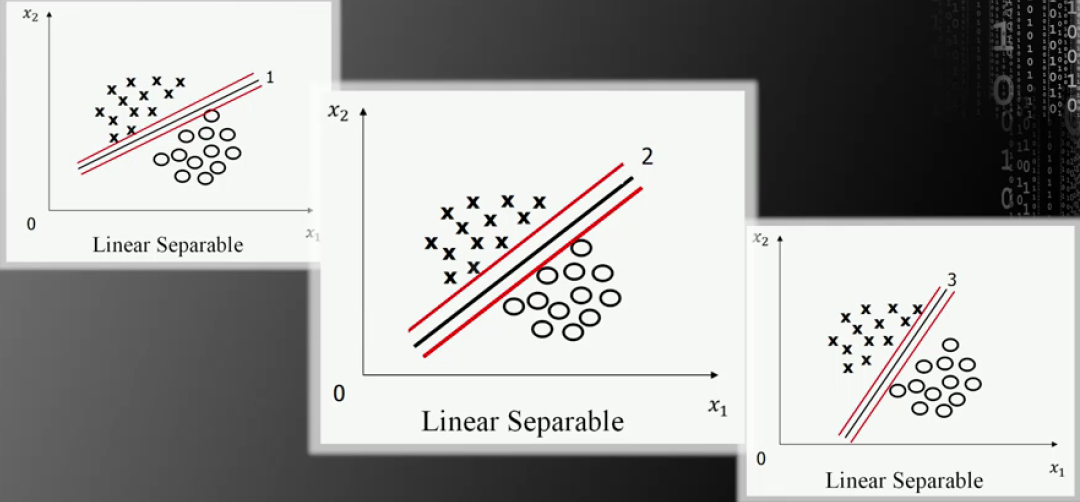
圖片來源:中國慕課大學《機器學習概論》
但僅根據間隔最大不能得出唯一的最優分類直線,例如,前文所述問題中,所有與2號線平行的線均為間隔最大的直線。因此,為可得出唯一直線,最優分類直線被限定處于穿過兩側支持向量的兩條直線中間的直線,即最優直線與兩側支持向量的距離相等。
綜上,支持向量機尋找的最優分類直線應滿足:
(1)該直線可將訓練數據完全分為兩類。
(2)該直線可最大化間隔。
(3)該直線處于間隔的中間,其與所有支持向量的距離相等。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20884
原文標題:機器學習相關介紹(7)——支持向量機(解決線性可分問題)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于改進支持向量機的貨幣識別研究
支持向量機在電力系統中的應用

基于支持向量機(SVM)的工業過程辨識
多分類孿生支持向量機研究進展
支持向量機的故障預測模型
人工智能之機器學習Analogizer算法-支持向量機(SVM)
介紹七本在注重打好數據科學的數學基礎上的技術讀物
什么是支持向量機 什么是支持向量




 Vladimir Vapnik創立支持向量機
Vladimir Vapnik創立支持向量機










評論