FFT 即快速傅立葉變換。在很多計算機領域都用用處,例如數字圖像處理、計算機網絡。但他在算法競賽中主要是用于多項式和生成函數相關的題目。
多項式
表達方式
簡介
- 系數表達式,即。
- 坐標形式。每一個坐標用表示。顯然,為了能夠表示一個確定的多項式,需要個不同的坐標來表示。
比較
- 對于系數表示,多項式加法的時間復雜度是,多項式乘法的時間復雜度是。
- 對于點值表示,多項式加法的時間復雜度同樣是,但是乘法的時間復雜度就是(因為多項式乘法以后最高項次數為,我們只需要個坐標表示)。
思考
這樣一來,我們就有一個想法,多項式乘法,是不是可以利用坐標表示做多項式乘法特別快這點來優化算法。
于是需要解決的最大的問題就是,多項式兩種表示方法之間的互相轉換。
求值樸素做法的時間復雜度是,即隨便選取一個值帶入,暴力計算。
差值樸素的做法時間復雜度是,即根據坐標進行高斯消元。
在介紹 FFT 之前,得先學習 DFT (離散傅里葉變換)算法。
DFT
由于對一個多項式的點值表達式的取是任意的,所以好的取法可能會使一個算法產生本質性的蛻變。
我們選取次單位復根作為來取值。
單位復根
,這個方程的復數根為次單位根。
單位的個單位根分別為。
個單位根在復平面的坐標表示為,我們將這個記為。在復平面上形象的表示的話,就是下圖:
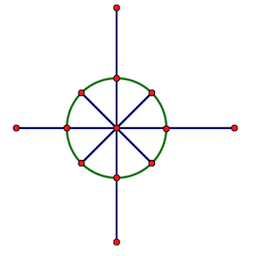
單位根在多項式的應用
我們將個單位根帶入多項式可以得到個因變量結果,記為。
我們將個單位根的倒數作為自變量帶入由作為系數的多項式,可以得到。
而當的時候,它為,其余時候,它為(通過等比數列求和)。于是有。
于是可以發現,將個單位根的倒數帶入變換后的多項式,可以得到原來的多項式。
這樣一來,我們利用個單位根的性質,完成了多項式兩種表示方式之間的轉換。
DFT算法
有了的取值,我們就可以得到的取值了。
。
直接暴力計算,兩個方向轉換的時間復雜均為。
FFT
那么 FFT 算法是如何優化計算這一過程的?利用分治。
我們把一個多項式的計算分為偶數項的計算和奇數項的計算:
也就是說, FFT 的思想就是不斷得把一個多項式拆分成奇數多項式和偶數多項式,然后合并兩個多項式的信息。
也就是說,如果我們已經得到了和,我們只需要就可以得到了。
每次都能把多項式的長度減小一半,于是時間復雜度就是。
模版
C++ 是自帶了復數 stl 的,即:
#include
但是常數大,跑得慢,不如自己重載的好。
- 下面的模版必須要保證是的整數次冪。
typedef double LD;
const LD PI = acos(-1);
struct C {
LD r, i;
C(LD r = 0, LD i = 0): r(r), i(i) {}
};
C operator + (const C& a, const C& b) {
return C(a.r + b.r, a.i + b.i);
}
C operator - (const C& a, const C& b) {
return C(a.r - b.r, a.i - b.i);
}
C operator * (const C& a, const C& b) {
return C(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r);
}
void FFT(C x[], int n, int p) {
for (int i = 0, t = 0; i < n; ++i) {
if (i > t) swap(x[i], x[t]);
for (int j = n >> 1; (t ^= j) < j; j >>= 1);
}
for (int h = 2; h <= n; h <<= 1) {
C wn(cos(p * 2 * PI / h), sin(p * 2 * PI / h));
for (int i = 0; i < n; i += h) {
C w(1, 0), u;
for (int j = i, k = h >> 1; j < i + k; ++j) {
u = x[j + k] * w;
x[j + k] = x[j] - u;
x[j] = x[j] + u;
w = w * wn;
}
}
}
if (p == -1)
FOR (i, 0, n)
x[i].r /= n;
}
void conv(C a[], C b[], int n) {
FFT(a, n, 1);
FFT(b, n, 1);
FOR (i, 0, n)
a[i] = a[i] * b[i];
FFT(a, n, -1);
}
例題
A * B II
https://acm.ecnu.edu.cn/problem/3007/
大整數相乘。
把每一位都看成是多項式其中一項的系數,那么大數最后的結果也就是多項式乘法系數的結果。
要進位處理。
Hnoi2017 禮物
顯然是要計算的最小值,其中$0≤x
展開這個式子,
除了,其他的和與相關的項都可以在的時間內算出了
那么配個方,就可以求出最小值了,而是固定的
現在的問題就是求,我們可以用FFT來解決
如果我們把多項式倒置,我們就能發現式子的和的下標和可以相同,我們可以利用多項式乘法同時算出卷積。
設,那么,這樣就可以用FFT算出來了
總的時間復雜度
#include
#define inf 0x3fffffff
using namespace std;
typedef double LD;
const LD PI=acos(-1);
struct C
{
LD r,i;
C(LD r=0,LD i=0):r(r),i(i){}
};
C operator + (const C& a, const C& b){
return C(a.r+b.r,a.i+b.i);
}
C operator - (const C& a, const C& b){
return C(a.r-b.r,a.i-b.i);
}
C operator * (const C& a, const C& b){
return C(a.r*b.r-a.i*b.i,a.r*b.i+a.i*b.r);
}
void FFT(C x[],int n,int p)
{
for (int i=0,t=0;i
-
圖像處理
+關注
關注
27文章
1293瀏覽量
56772 -
FFT
+關注
關注
15文章
434瀏覽量
59403 -
計算機網絡
+關注
關注
3文章
339瀏覽量
22179 -
傅立葉變換
+關注
關注
3文章
105瀏覽量
32404
發布評論請先 登錄
相關推薦
如何使用快速傅立葉變換(FFT)的8590 C/E/L系列頻譜分析儀中的FFT函數?
淺懂示波器FFT快速傅立葉變換功能及運用
示波器FFT快速傅立葉變換不會用?看完這篇帖子,我徹底悟了
快速傅立葉變換開發指南
快速傅立葉變換(FFT)的Nios II實現
基于FPGA的快速傅立葉變換
傅立葉變換是怎么變換的 傅立葉的理解
淺懂示波器FFT快速傅立葉變換功能及運用
如何使用SBench 6對數字化儀采集信號進行處理?(三)——快速傅立葉變換(FFT)
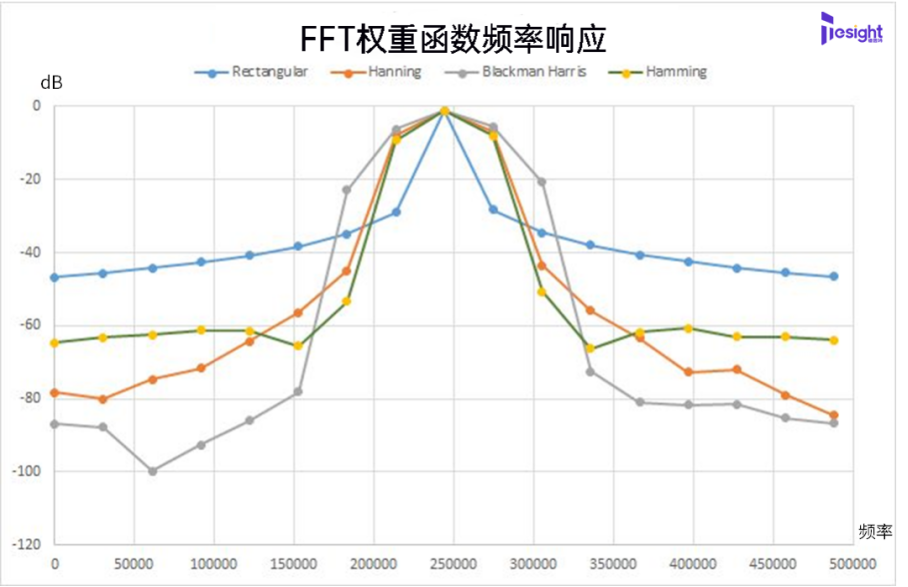




 看完學會速傅立葉變換FFT
看完學會速傅立葉變換FFT










評論