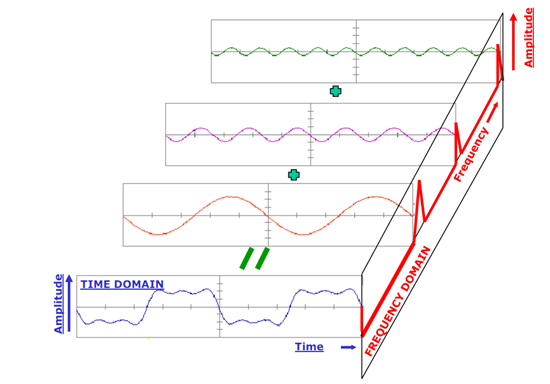
FFT是計算DFT的快速算法，但是它是基于復數(shù)的，所以計算實數(shù)DFT的時候需要將其轉換為復數(shù)的格式，下圖展示了實數(shù)DFT和虛數(shù)DFT的情況，實數(shù)DFT將時域中N點信號轉換成2個(N/2+1)點的頻域信號，其中1個(N/2+1)點的信號稱之為實部，另一個(N/2+1)點的信號稱之為虛部，實部和虛部分別是正弦和余弦信號的幅度。

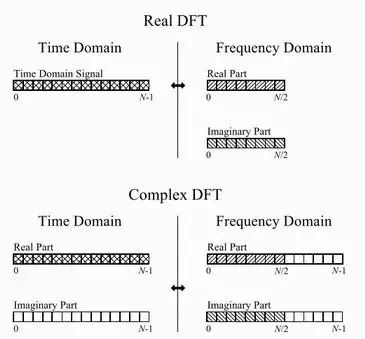
相比較而言，復數(shù)DFT將2個N點的時域信號轉換為2個N點的頻域信號。時域和頻域中，1個N點信號是實部，另1個N點信號是虛部。

如果要計算N點實數(shù)DFT，則將這個N個點作為時域中的實部，另取N個0點作為時域的虛部，用FFT計算這樣一個復數(shù)信號的DFT得到2個N點的頻域信號，1個N點是實部另1個N點是虛部，在這兩個N點的信號中，從0到N/2個點就是須計算的N點實數(shù)的DFT頻域。

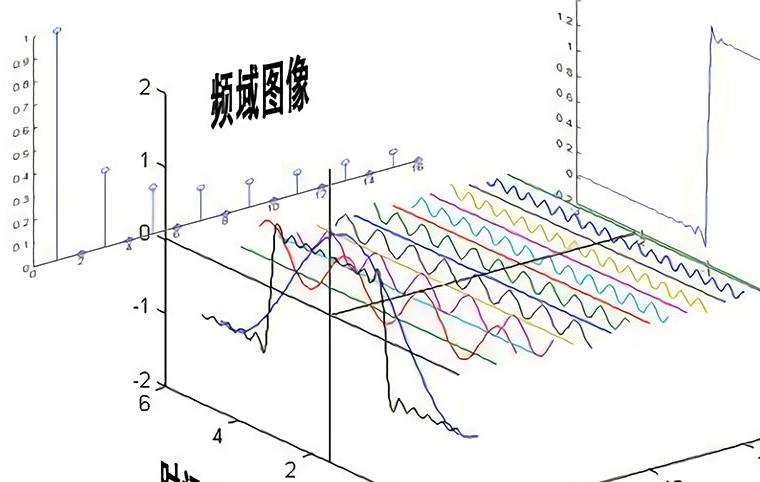
對于實數(shù)DFT來說，它的頻域也是離散周期信號，其周期為N點，從0到N/2點和1-N到-1點具有對稱性，這個你可以從下面一張圖看出。圖中坐標不是用N表示，是用采樣頻率的分數(shù)表示。

所以你如果用FFT反變換計算的是實數(shù)時域，則要滿足上圖的對稱性。

FFT如何工作

◤

FFT的計算可以分為三步：首先將1個N點的時域信號分成N個1點的時域信號，然后計算這N個1點時域信號的頻域，得到N個頻域的點，然后將這個N個頻域的點按照一定的順序加起來，就得到了我們需要的頻譜。這里每個點的意思是復數(shù)，都有實部和虛部。

• 第一步的信號分解按照下面的規(guī)律執(zhí)行：

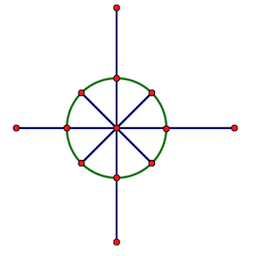
可以看出它是按照比特反轉順序來分解的。

• 第二步是計算每個點的頻譜：

這一步很簡單，因為一個時域的點的頻譜的數(shù)值就是它自己，所以這一步什么也不需做，但需明白這時候N個點不是時域信號了，而是頻域信號。

• 第三步是將這N個頻域信號結合起來

這一步是最麻煩的一步。就是和前面時域分解的順序相反，將2個1點的頻域信號變成1個2點的頻域信號，再將2個2點的頻域信號變成1個4點的頻域信號，一直到結束。這里看下如何將2個4點的頻域信號變成1個8點的頻域信號。

首先對1個4點的頻域信號進行復制，這樣能稀釋時域信號，也對另1個4點的頻域信號進行復制，不過復制之前需要乘上正弦函數(shù)，這樣得到的稀釋時域信號時經過了平移的，然后將這兩個頻域信號加起來，如下圖所示。之所以這么做的目的是在時域分解的時候就是用這種交織的分解方式的。

以下是基本的運算，稱為蝶形運算，它將2個1點的復數(shù)變成1個2點的復數(shù)。

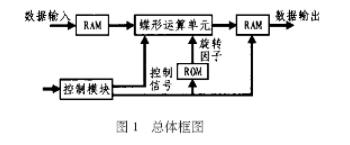
FFT運算的流程圖

運算速度比較

• 如果用相關方法計算DFT：

• 如果用FFT方法計算DFT：

不過，F(xiàn)FT的速度還能更快。 比如使用基4或者基8，這樣不是2點一計算，而是4點或者8點一計算，可以提高速度。

FFT對DSP來說就像是晶體管對電子學來說，都是領域的基礎，每個人都知道怎么使用它們，但是只有很少一部分真正了解它們的原理。

事實就是這樣，你只要知道怎么用就可以了。