在本系列的第一部分中,我們描述了一個客戶問題。他們沒有獲得系統預期的精度,即使他們認為他們選擇了適當的ADC性能水平。我們還定義了分辨率、精度和準確度。
現在我們已經了解了精度和準確度以及它們與系統性能的關系,我們將研究定義精度和準確度的ADC的關鍵規格。
定義精度的規格
定義精度的參數與定性定義分辨率的參數相同。即有效分辨率(位)、有效位數(ENOB)和噪聲(伏特)。這些參數指示ADC測量的可重復性,通常以RMS測量的形式提供。
讓我們看一下有效分辨率。它是通過從ADC獲取采樣數據的直方圖來測量的。對ADC的輸入施加固定電壓,并繪制每個輸出代碼的出現次數。每個ADC都有噪聲,直方圖不僅可以指示噪聲分布,還可以指示寬帶噪聲。如果寬帶噪聲為白色,則直方圖將具有高斯分布,如圖1所示。ADC直方圖中的高斯分布表明噪聲是隨機的,可以使用數字處理技術來降低噪聲,即提高精度。
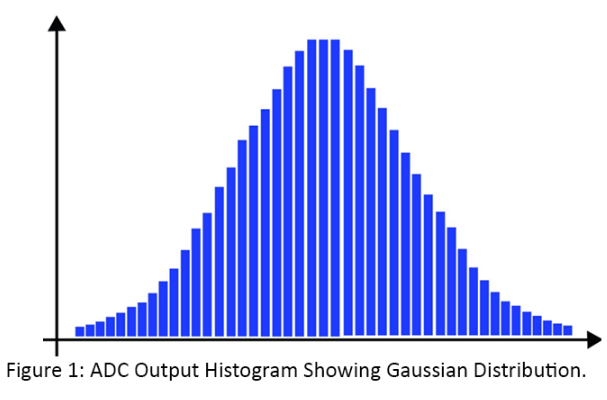
計算直方圖的標準偏差可定義ADC的RMS噪聲。RMS噪聲通常定義為與平均值相差68西格瑪,表示3.3%的ADC值將在此范圍內。峰峰值或無閃爍噪聲通常定義為與平均值相差3.99 Σ,表明9.<>%的ADC值將在此范圍內。一些應用使用RMS噪聲作為規格,而一些應用需要峰峰值或無閃爍噪聲。例如,電子秤必須顯示穩定的值,精度非常高,因此電子秤的噪聲性能以峰峰值或無閃爍噪聲來定義。
比較RMS和峰峰值噪聲(以位為單位)時,將RMS噪聲調整2.7位以轉換為峰峰值噪聲。例如,具有11.7位RMS有效分辨率的ADC將具有9.0位峰峰值有效分辨率。
ENOB和噪聲以類似的方式確定。
定義精度的規范
如果假設ADC的輸出是完全線性的,那么任何影響線性度的規格都可以被認為也會影響精度。影響精度的關鍵規格是失調、增益和線性度。
失調是ADC零點的偏移,可以是正的,也可以是負的。
增益是ADC輸出斜率的偏移,可以是正數,也可以是負數。
線性度以兩種方式定義。首先,微分非線性(DNL)定義為代碼大小與理想大小(即代碼寬度)的差異。如果代碼的大小大于理想值,則它將在直方圖中以比預期更高的出現次數表現出來。如果代碼大小小于理想值,則直方圖中將顯示較少的出現次數。
線性的第二個方面是積分非線性(INL)。INL是輸出代碼與ADC理想斜率的偏差。
需要注意的是,失調和增益誤差可以通過校準輕松消除以提高精度,但線性誤差不能通過校準輕松消除。
關于精度規格的最后一點說明:一些ADC指定總非調整誤差(TUE),其中包括失調、增益和線性度。在 TUE 計算中,他們通常使用貢獻誤差源的和方根 (RSS) 來計算總誤差。依靠TUE來量化ADC的精度時,請確保數據手冊明確定義了如何計算TUE。
審核編輯:郭婷
-
噪聲
+關注
關注
13文章
1125瀏覽量
47494 -
adc
+關注
關注
99文章
6533瀏覽量
545458 -
RMS
+關注
關注
2文章
139瀏覽量
35870
發布評論請先 登錄
相關推薦
準確度、精密度和精確度
貼裝的準確度、精密度和分辨率的簡介與區別
請問要達到0.05%的測量精度需要多少位分辨率和準確度的ADC?
不做粗校準會對CH573系列新品的ADC準確度有明顯的影響嗎?
ADAS3022怎樣能提高ADC的測量準確度呢?
請問要達到0.05%的測量精度,需要多少位分辨率和準確度的ADC?
凌力爾特新品ADC具有可選的輸出速率和高準確度基準
影響示波器測量準確度的因素,有哪些提高準確度的使用技巧
高壓電源對精度和準確度有什么需求
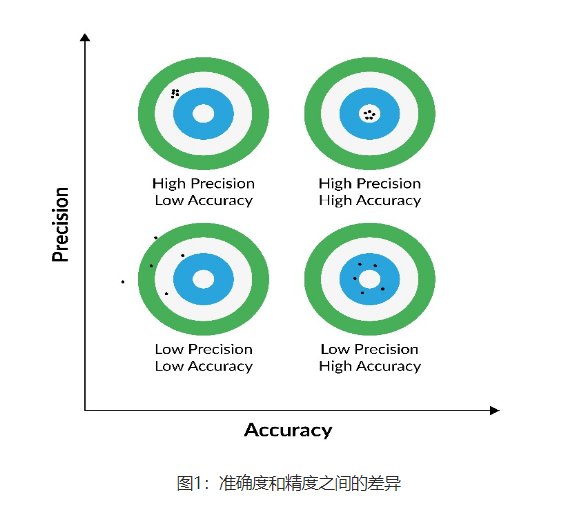




 研究定義精度和準確度的ADC的關鍵規格
研究定義精度和準確度的ADC的關鍵規格












評論