通常我們在控制小車運動的時候不知道如何精確的對小車軌跡進行控制。在不懂得小車控制算法精髓的時候，我們是無法對小車進行精確的控制的。目前絕大多數小車都是用PID控制算法來實現對小車的運動控制的。現在很多玩家就只知道一種調節方法，就是比例調節，即向左偏就向右調節，向右偏就向左調節，最容易想到，也是最容易用軟硬件實現的，但是結果也是最容易出問題的。當時的感覺就是小車太靈敏了，忽左忽右，不是很穩定。后來查了資料后知道了其他的調節方式。

控制算法：

電機控制算法的作用是接受指令速度值，通過運算向電機提供適當的驅動電壓，盡快地和盡快平穩地使電機轉速達到指令速度值，并維持這個速度值。換言之，一旦電機轉速達到了指令速度值，即使在各種不利因素(如斜坡、碰撞之類等使電機轉速發生變化的因素)的干擾下也應該保持速度值不變。為了提高機器人小車控制系統的控制精度，選用合適的控制算法顯得十分必要。控制算法是任何閉環系統控制方案的核心，然而并非越復雜、精度越高的算法越好，因為比賽要求非常高的實時性，機器人必須在非常短的時間內作出靈敏的反應，所以現代的一些先進控制算法，比如模糊控制、神經元網絡控制等就不能應用到小車控制系統里。本系統選用了最常規、最經典的PID控制算法，通過實際應用取得了很好的效果。下圖是PID控制原理結構圖。

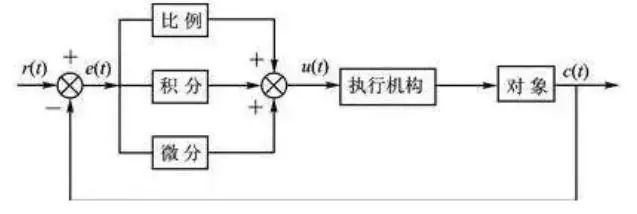
圖 PID控制系統原理結構框圖

1 比例項

控制回路中的第一個偏差轉換環節就是比例項。這一環節簡單地將偏差信號乘以常數K 得到新的CV值(值域為-100~100)。基本的比例控制算法如下：

loop:

PV=ReadMotorSpeed()

Error=SP-PV

CV=Error*Kprop

Setpwm(cv)

Goto loop

其中SP為設定值，PV為反饋值，Error為誤差。

上一段程序中的SetPWM()函數并非將CV值作為絕對的PWM占空比來對待。否則，不斷降低的偏差值會使輸出值接近零，而且由于電機工作時需要持續的PWM信號，控制系統將會使電機穩定在低速運轉狀態上，從而導致控制系統策略失敗。

相反，CV值一般被取作當前PWM占空比的改變量，并被附加到當前的PWM占空比上。這也要求SetPWM()函數必須將相加后得到的PWM占空比限制在0%~100%。正的CV值將使電機兩端電壓增加。負的CV值將使電機兩端電壓降低。如果CV值等于0，則無需改變但前占空比。較低的K 值會使電機的速度響應緩慢，但是卻很平穩。較高的K 值會使速度響應更快，但是卻可能導致超調，即達到穩定輸出前在期望值附近振蕩。過高的K 值會導致系統的不穩定，即輸出不斷震蕩且不會趨于期望值。

2 積分項

積分正好與微分相對。假如有一個描述變化率(微分)的表達式，那么對該表達式的積分就將得到隨時間變化的原物理量。如加速度的積分是速度，速度的積分是位移。

在PID控制回路中，偏差的積分代表從控制開始時算起所有偏差積累的總和。該總和被常數K 所乘后再添加到回路輸出中。在回路中，如果沒有積分環節，盡管控制系統也會趨于穩定，但是由于某種原因輸出值可能最終也無法達到SP值。

一個簡單但完全的PID控制器地偽代碼實現如下：

loop:

PV=ReadMotorSpeed()

LastError=Error

Isum=Isum+Error

Error=SP-PV

Rate=Error-LastError

CV=Error*Kprop+Krate*Rate+Kint*Isum

SetPWM(CV)

Goto loop

由于積分項會越來越大，這就會使控制回路在SP值的改變時響應變慢，某些應用場合在CV值達到取值邊界(如為：-100~100)時會停止累加Isum。在SP值改變時，也可以除去Isum項。

3 微分項

任何變量的微分項被用來描述該變量是如何相對于另一個變量(多位時間)變化的。換句話說，任何變量的微分項就是它隨時間的變化率。如位移隨時間的變化率是速度。速度相對于時間的微分是加速度。

在PID控制器中，值得關心的是偏差信號相對于時間的微分，或稱變化率。絕大多數控制器將微分項定義為：

Rate=(E-E )/T

式中，E為當前偏差，E 為前次偏差值，T為兩次測量的時間間隔。負的變化率表明偏差信號的改善。當微分項被具體應用于控制器中時，將一個常數乘以該微分項，并將它加到比例項上，就可以得到最終的CV值計算公式：

CV=( K E)+( K Rate)

當偏差信號接近零時，CV值將為負，所以當偏差信號開始改善時，微分項的作用將逐漸減弱校正輸出量。在某些場合下，微分項還有利于超調量的消除，并可以允許使用較大的K 值，從而可以改善響應的快速性。微分環節還預示了偏差信號的變化趨勢。當控制對象對控制器的輸出響應遲緩時，微分環節的作用尤為明顯。

含有微分項的控制算法的偽代碼實現如下：

loop:

PV=ReadMotorSpeed()

LastError=Error

Error=SP-PV

Rate=Error-LastError

CV=Error*Kprop+Krate*Rate

SetPWM(CV)

Goto loop

4 PID的整定方法

在整定PID控制器參數時，可以根據控制器的參數與系統動態性能和穩態性能之間的定性關系，用實驗的方法來調節控制器的參數。有經驗的調試人員一般可以較快地得到較為滿意的調試結果。在調試中最重要的問題是在系統性能不能令人滿意時，知道應該調節哪一個參數，該參數應該增大還是減小。

為了減少需要整定的參數，首先可以采用PI控制器。為了保證系統的安全，在調試開始時應設置比較保守的參數，例如比例系數不要太大，積分時間不要太小，以避免出現系統不穩定或超調量過大的異常情況。給出一個階躍給定信號，根據被控量的輸出波形可以獲得系統性能的信息，例如超調量和調節時間。應根據PID參數與系統性能的關系，反復調節PID的參數。

如果階躍響應的超調量太大，經過多次振蕩才能穩定或者根本不穩定，應減小比例系數、增大積分時間。如果階躍響應沒有超調量，但是被控量上升過于緩慢，過渡過程時間太長，應按相反的方向調整參數。

如果消除誤差的速度較慢，可以適當減小積分時間，增強積分作用。

反復調節比例系數和積分時間，如果超調量仍然較大，可以加入微分控制，微分時間從0逐漸增大，反復調節控制器的比例、積分和微分部分的參數。

總之，PID參數的調試是一個綜合的、各參數互相影響的過程，實際調試過程中的多次嘗試是非常重要的，也是必須的。

具體有以下幾種方法：

（1）試湊法

試湊法就是人工選擇PID參數，使控制系統響應達到預定要求，這種方法既簡單又復雜，說簡單是，如果你有經驗和運氣的話，那么在SIMULINK中，可能很快就達到了目標，說難的是，在現場實戰中，可能費了很大時間和精力來調整三個參數，也沒有完成任務。

（2）臨界比例度法

臨界比例度法就是僅在P作用下，調整比例度使系統等幅振蕩，然后根據公式算出PID值，效果如圖1所示，圖中左半部分是系統等幅振蕩，右半部分是控制效果。下圖是通過MATLAB 仿真的PID臨界比例度法控制的曲線效果圖。

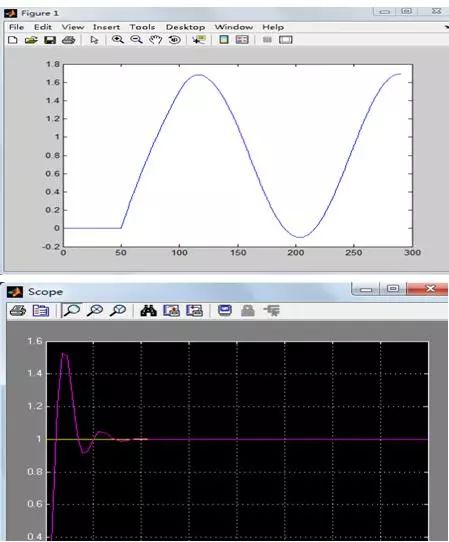
圖1 PID臨界比例度法控制的曲線

（3）衰減曲線法

衰減曲線法 就是僅在P作用下，調整比例度使系統響應曲線以4:1或10:1比率衰減，然后根據公式算出PID值，效果如圖2所示，圖中左半部分是系統衰減曲線，右半部分是控制效果。下圖是通過MATLAB 仿真的PID衰減曲線法控制的曲線效果圖。

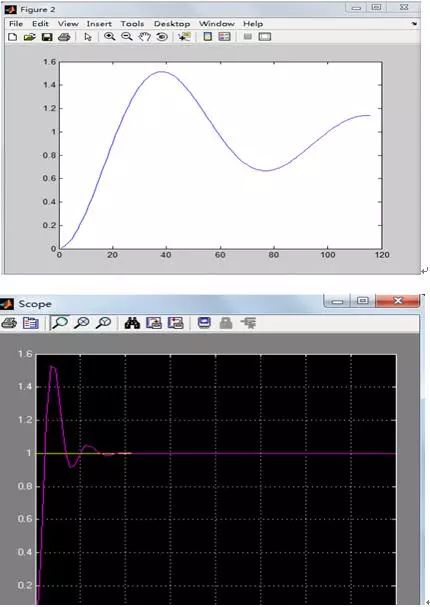
圖2 PID衰減曲線法控制的曲線

（4）反應曲線法

反應曲線法就是在開環狀態下，加階躍信號，然后用一階加純滯后系統逼近原系統，然后根據由Z-N或C-C公式算出PID值，效果如圖3所示，圖中左半部分是系統 響應曲線 ， 右半部分是控制效果。圖4是一個三階系統，臨界比例度法 求得的有關參數。下圖是通過MATLAB 仿真的PID反應曲線法控制的曲線效果圖。

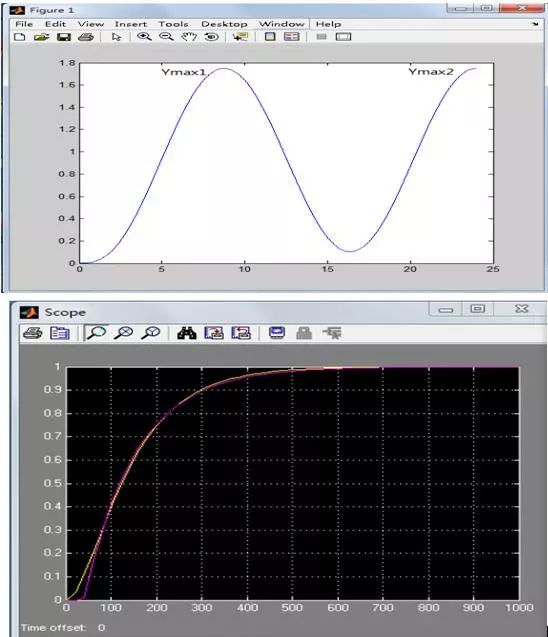
圖3 PID反應曲線法控制的曲線

審核編輯：湯梓紅